JUMP TO TOPIC
 To know what is the additive inverse of the polynomial, we solve for the polynomial that results from negating all of the terms in the original polynomial. In other words, the additive inverse of a polynomial is the polynomial that has the same coefficients as the original polynomial but with the opposite sign. Additive inverses are used in mathematical operations such as addition and subtraction and are also used in many areas of physics and engineering. In this article, we will learn how to solve for the additive inverses of any polynomial and many examples with step-by-step solution guides.
To know what is the additive inverse of the polynomial, we solve for the polynomial that results from negating all of the terms in the original polynomial. In other words, the additive inverse of a polynomial is the polynomial that has the same coefficients as the original polynomial but with the opposite sign. Additive inverses are used in mathematical operations such as addition and subtraction and are also used in many areas of physics and engineering. In this article, we will learn how to solve for the additive inverses of any polynomial and many examples with step-by-step solution guides.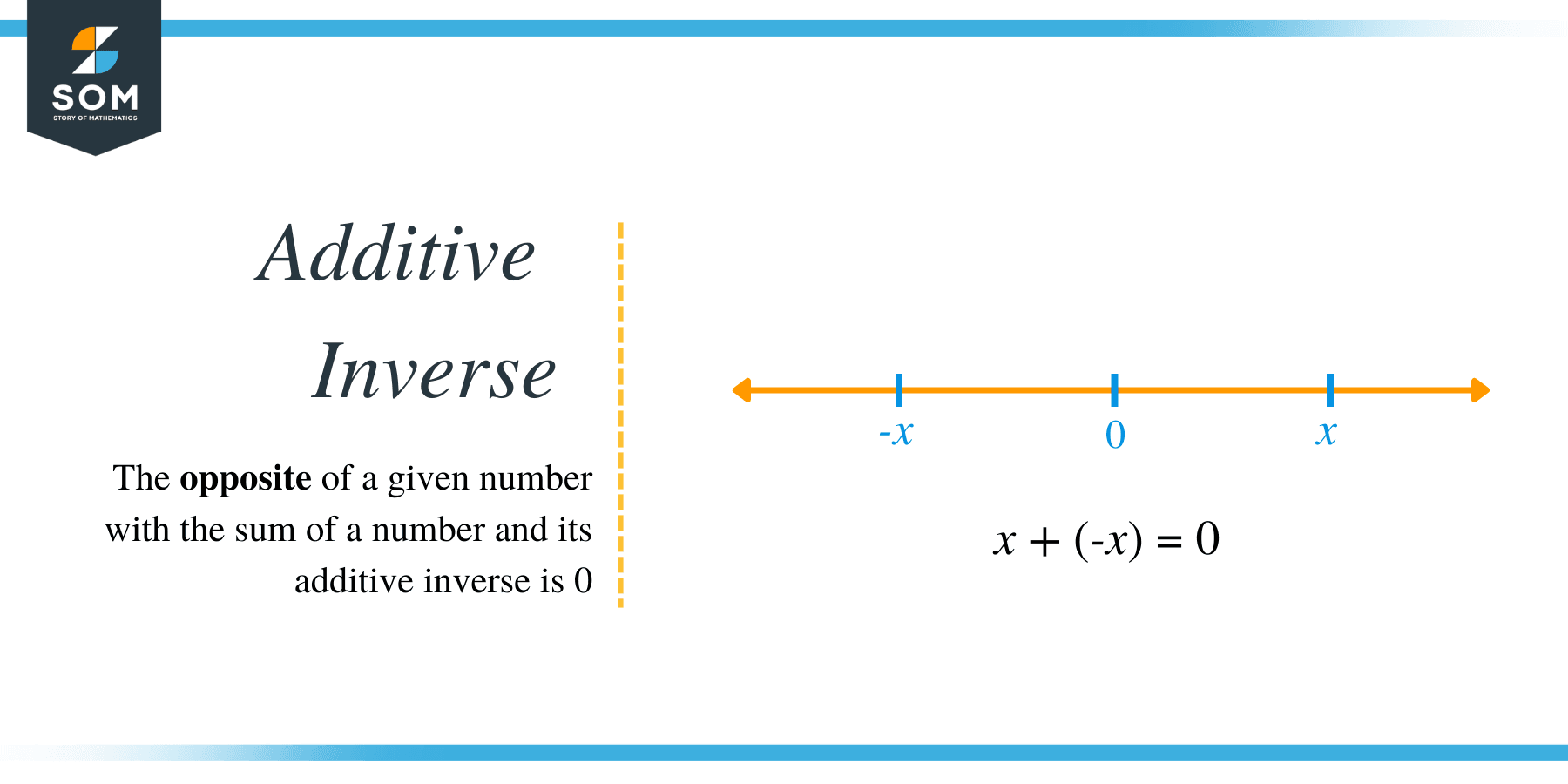
What Is the Additive Inverse of a Polynomial?
How To Find the Additive Inverse of a Polynomial?
To find the additive inverse of a given polynomial, you need to negate every term of the polynomial. The additive inverse is the resulting polynomial when you multiply negative or oppose the sign of each term of the original polynomial so that the resulting sum of the two polynomials is equal to zero. For instance, we have the polynomial $2xy+3x-y$. Multiplying negative to the polynomial will give us:
\begin{align*}
-(2xy+3x-y)&= -2xy-3x-(-y)\\
&=-2x-3x+y.
\end{align*}
Thus, the additive inverse of $2xy+3x-y$ is $-2xy-3x+y$.
We can also easily verify that if the additive inverse of the polynomial is indeed its additive inverse. We just need to add the two polynomials, the original polynomial and the additive inverse we obtained. If their sum is equal to zero, then the obtained additive inverse is correct. We verify that the additive inverse of $2xy+3x-y$ is $-2xy-3x+y$.
\begin{align*}
&(2xy+3x-y)+(-2xy-3x+y)\\
&=(2xy-2xy)+(3x-3x)+(-y+y)\\
&=0+0+0\\
&=0.
\end{align*}
Hence, the additive inverse we obtained is correct.
Examples of Solving for Additive Inverse of a Polynomial
Example 1
- Solve for the additive inverse of the polynomial -4xy+3z+1.
Negating the whole polynomial, we have:
\begin{align*}
-(-4xy+3z+1)&=-(-4xy)-(3z)-(1)\\
&=4xy-3z-1.
\end{align*}
Thus, the additive inverse of $-4xy+3z+1$ is the polynomial $4xy-3z-1$.
To verify, we add the two polynomials and see that their sum is equal to zero.
\begin{align*}
(-4xy+3z+1)+(4xy-3z-1)&=(-4xy+4xy)+(3z-3z)+(1-1)\\
&=0+0+0\\
&=0.
\end{align*}
Example 2
- What is the additive inverse of $3x-z+4xy^2-2$?
Take note the signs of each term and negate them.
| Terms of the polynomial | Negated term |
|---|---|
| $3x$ | $-3x$ |
| $-z$ | $+z$ |
| $4xy^2$ | $-4xy^2$ |
| $-2$ | $+2$ |
Example 3
- Find the additive inverse of $-2pq+3p^2 q+9pq^2-6-4p$.
We can multiply the multiply by negative one to solve for its additive inverse. Thus, we have:
\begin{align*}
-(-2pq+3p^2 q+9pq^2-6-4p)&=-(-2pq)-(3p^2 q)-(9pq^2 )-(-6)-(-4p)\\
&=2pq-3p^2 q-9pq^2+6+4p.
\end{align*}
Hence, the additive inverse of the given polynomial is $2pq-3p^2 q-9pq^2+6+4p$.
Example 4
- Is $x-y$ the additive inverse of $x+y$?
To check if the $x-y$ is the additive inverse of $x+y$, we need to take their sum. Thus, we have:
\begin{align*}
(x+y)+(x-y)&=(x+x)+(y-y)\\
&=2x+0\\
&=2x.
\end{align*}
Since the sum of the two polynomials is not zero, then $x-y$ is not the additive inverse of $x+y$. The real additive inverse is $-x-y$ because
\begin{align*}
(x+y)+(-x-y)&=(x-x)+(y-y)\\
&=0+0=0.
\end{align*}
Why Are Additive Inverses of a Polynomial Important?
Example 5
Example 6
FAQ
What Is the Additive Inverse of the Polynomial? -7y2+x2y-3XY-7x2
What Is the Additive Inverse of the Polynomial -9xy2+6x2y-5x3
What Is the Additive Inverse of the Polynomial -6x^3+4x^2-4x
What Is the Additive Inverse of the Polynomial 9xy2+6x2y
What Is the Additive Inverse of the Polynomial 3
Conclusion
The additive inverse is useful in mathematics because it allows us to cancel out terms. This article provided examples of how to find the additive inverse of a polynomial and showed why it is important. We summarized the important points that can be noted in the topic.
- The additive inverse of a polynomial is the polynomial that results from negating each term of the original polynomial.
- The sum of the polynomial and its inverse is equal to zero.
- To find the additive inverse of the polynomial, you just need to change the sign of each term or multiply the original polynomial by $-1$.
- Additive inverses of polynomials are important because it helps simplify expressions.
The examples discussed in this article are easy to follow and can be used as a reference when solving equations. The additive inverse of a polynomial is an easy concept to learn and is important for a variety of mathematical operations.
