2pir – Comprehensive Explanation and Detailed Examples - The Story of Mathematics - A History of Mathematical Thought from Ancient Times to the Modern Day

2pir is the circumference of a circle.

The circumference (or the perimeter) of a circle is the total length of the circle’s boundary. The circumference is a linear measure, and its units are mostly given as centimeters, meters or inches.

A circle is a closed round figure, and all the points on the circle’s boundary are equidistant from the center of the circle. In geometry, we are only interested in calculating the area and circumference of the circle. In this topic, we will discuss the circumference of the circle, its proof and related examples.

What Is 2pir?

$2\pi r$ is the formula for the circumference of a circle, and the circumference of a circle is the product of two constants: “$2$” and “$\pi$;” while “$r$” is the radius of the circle.

You will also encounter the question is 2pir area of the circle? The answer to this question is no, the area of the circle is $\pi r^{2}$.

If we cut open a circle, put it in a straight line, and measure its length, it will give us the total length of the boundary of a circle. As the circle is a closed figure and we need a formula for calculating the total boundary of the circle, this is where the formula helps us.

We should use the important elements of the circle used to calculate the area and circumference of the circle and these important elements.

1. Center of the circle

2. Diameter of the circle

3. Radius of the circle

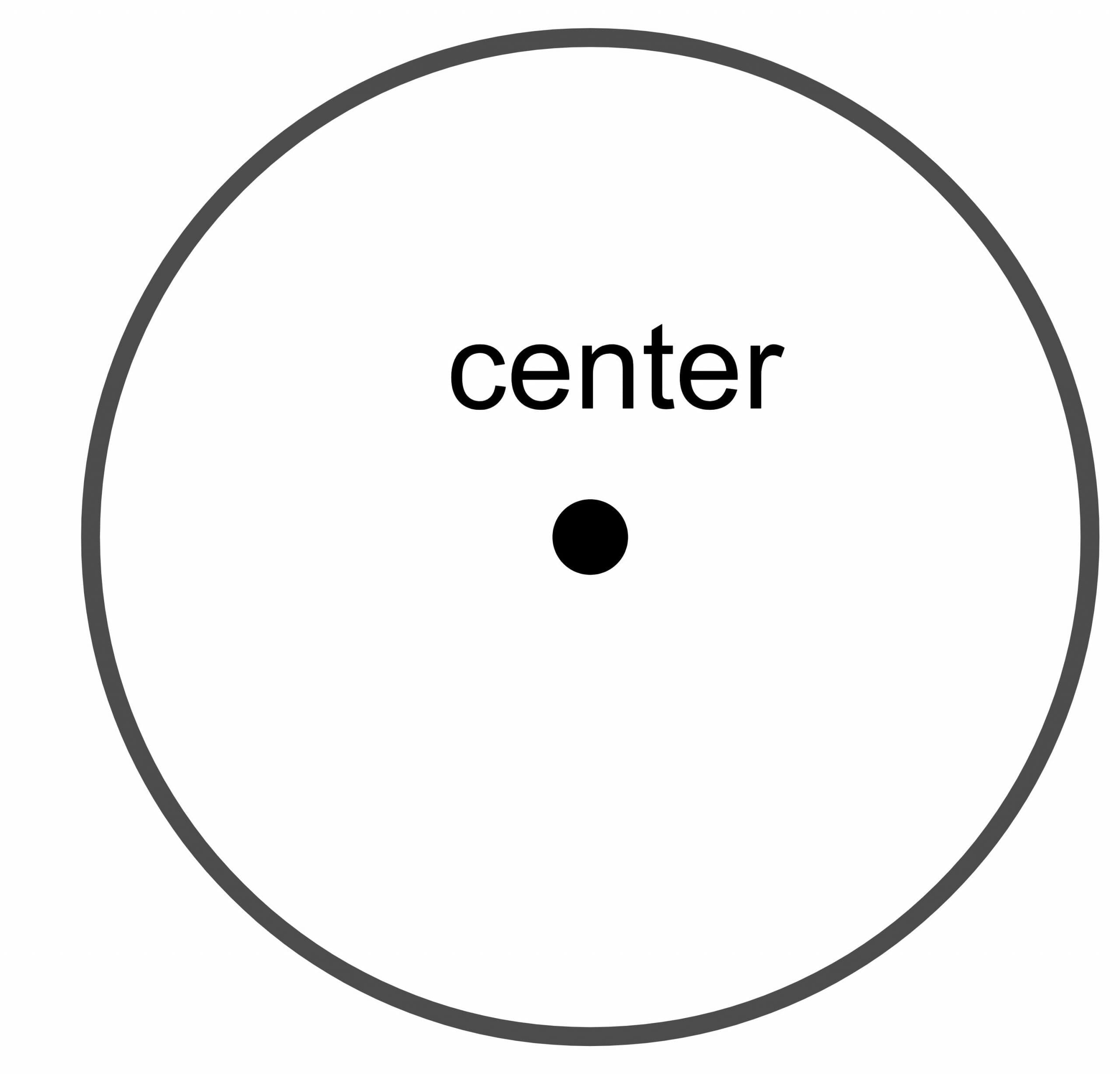
Center of the circle: The center of the circle is the fixed point of the circle situated equidistant from every point on the boundary of the circle.

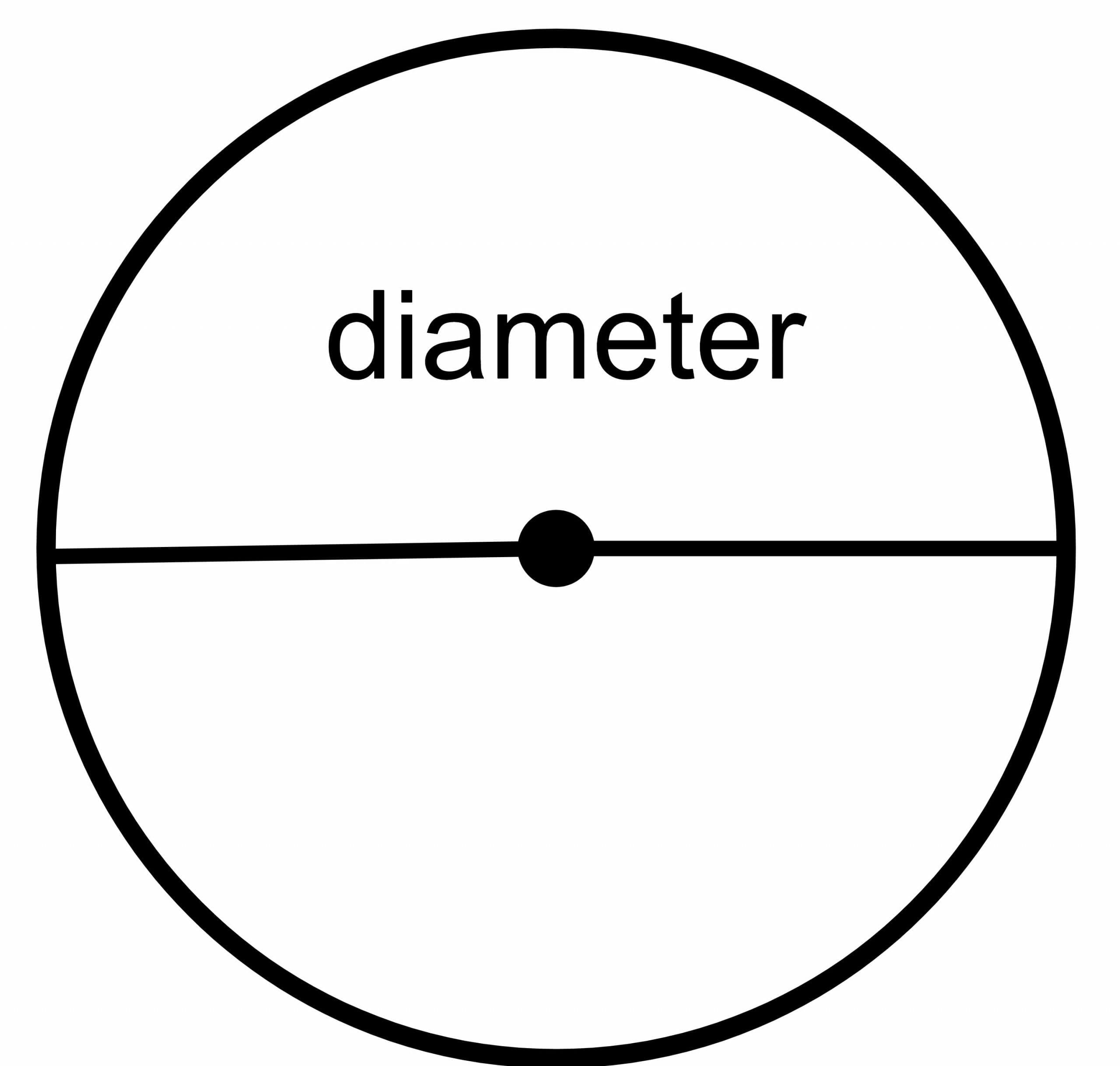
Diameter of the circle: The circle’s diameter is the total distance from one point of the circle to the other point, provided the drawn line crosses the center of the circle. So it is a line that touches different ends or boundaries of the circle while passing through the center. It is denoted as “ $\dfrac{r}{2}$.”

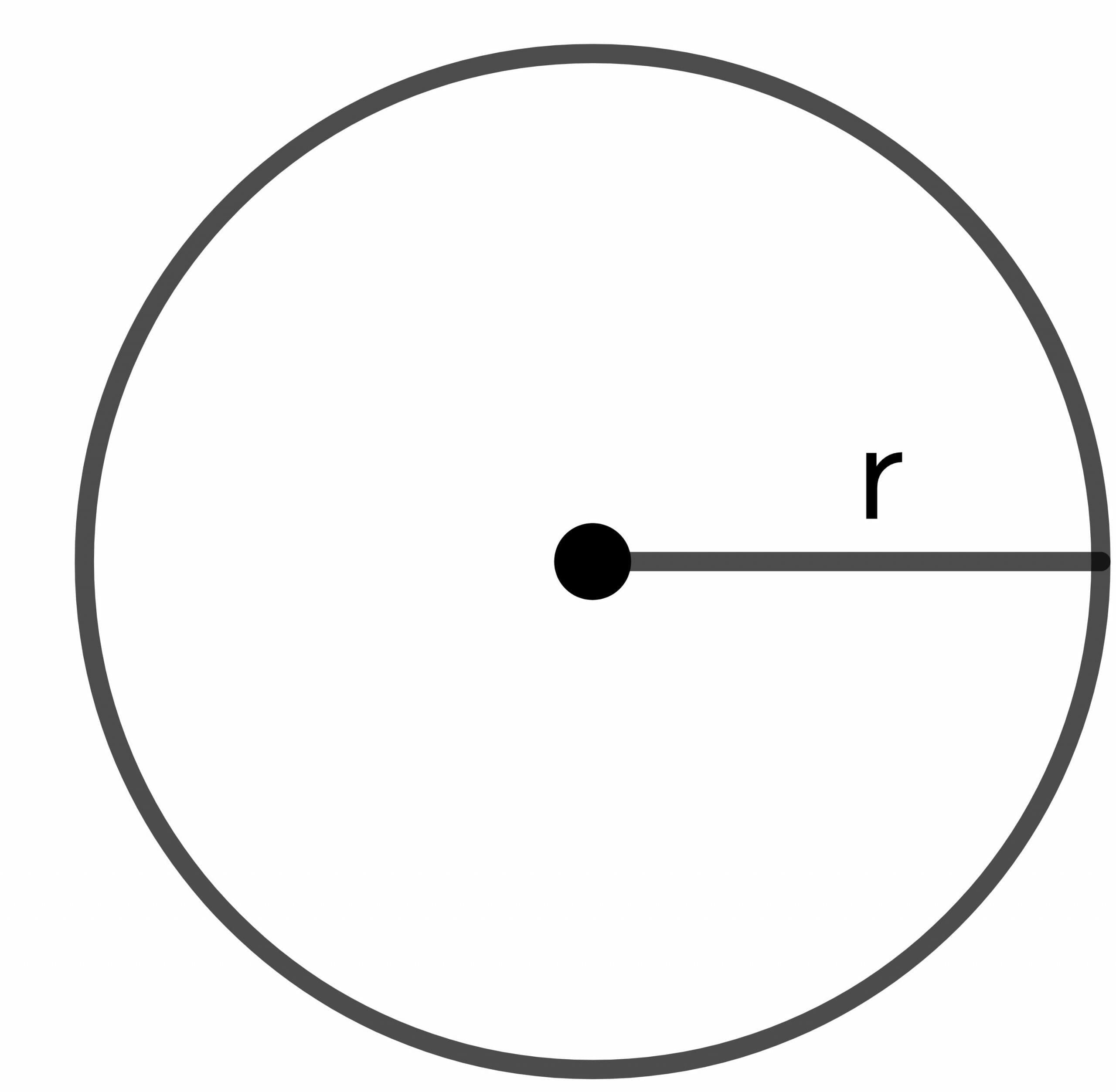
Radius of the circle: The circle’s radius is the total distance from any point on the boundary of the circle to the center of the circle and is represented as “$r$”.

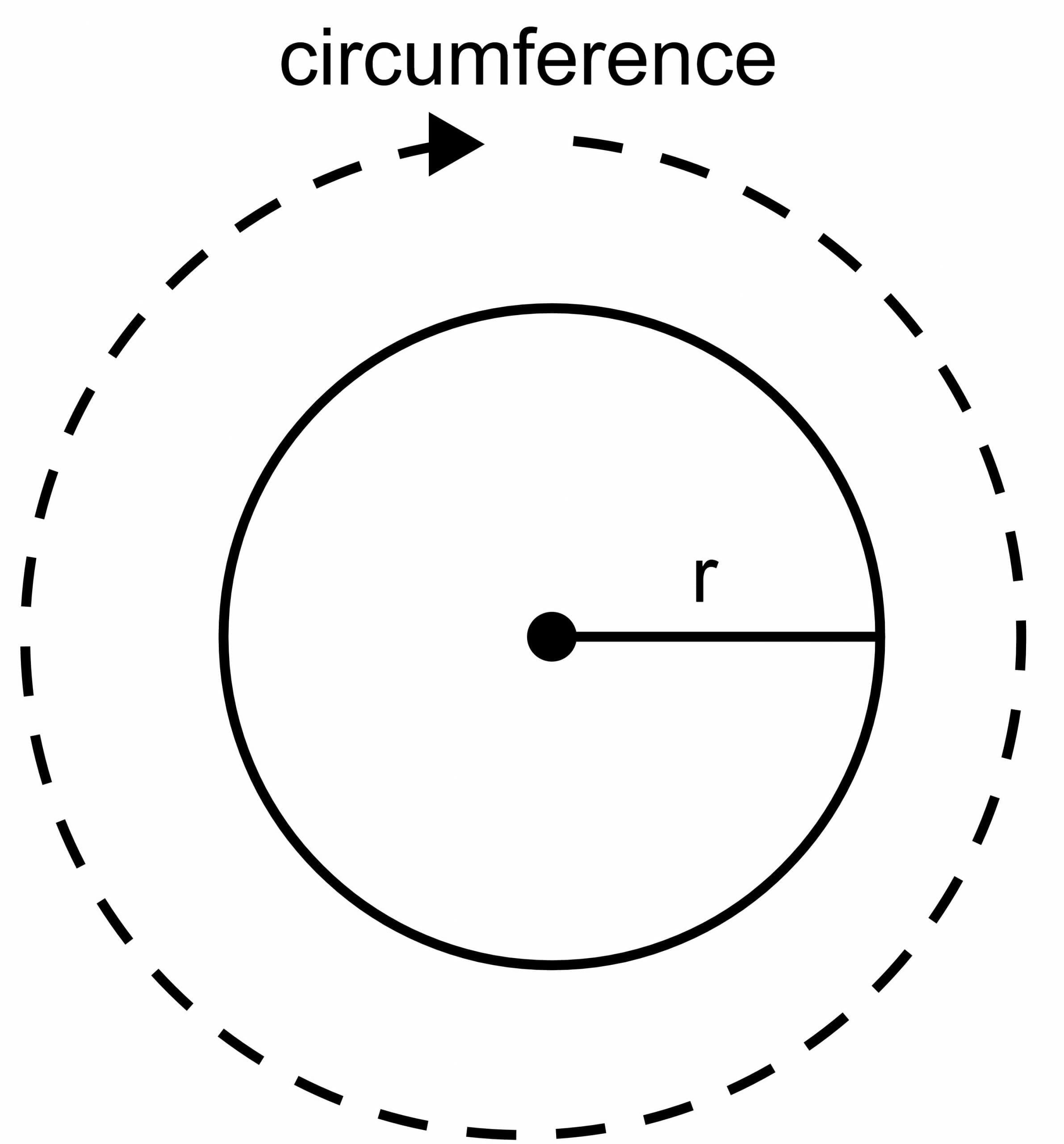
How To Prove That the Circumference of a Circle Is 2pir

The circumference of the circle is the total length of the boundary of the circle, and it cannot be calculated by using a ruler or scale as we do for other geometrical figures. The circle has a curved shape, and we have to use the formula to calculate the circle’s circumference. In deriving the 2pir formula as the circumference of the circle, we use a constant value $\pi$ and a variable value of radius “$r$”.

The $\pi$ has a constant value of $3.14159$ or $\dfrac{22}{7}$. The value of $\pi$ is ratio of the circumference of the circle to the diameter of the circle.

$\pi = \dfrac{C}{D}$ (1)

Here,

C = circumference of the circle

D = Diameter of the circle

The formula for the diameter of the circle is given as:

$D = \dfrac{r}{2}$

So, plugging the value of “D” in equation “1”:

$\pi = \dfrac{C}{(\dfrac{r}{2})}$

$C = 2.\pi.r$

Hence, the circumference of the circle is given as $2.\pi.r$

Alternative Proof

Consider a circle having a centered origin with radius “r” in an X-Y plane.

We can write the equation for the circle as:

$x^{2} + y^{2} = r$

Where

x = point on X-axis

y = point on Y-axis

r = radius of the circle

If we only take the first quadrant part of the circle, then we can obtain the length or arc of the line of the circle.

$L = 4 \int_{a}^{b}\sqrt{(x^{‘}(\theta))^{2}+ (y^{‘}(\theta))^{2}}$

Here,

$x = r.cos\theta$

$y = r.sin\theta$

$x^{‘}(\theta) = -r.sin\theta$

$y^{‘}(\theta) = r.cos\theta$

$L = 4 \int_{a}^{b}\sqrt{(-r.sin\theta)^{2}+ (y^{‘}(r.cos\theta)^{2}}$

$L = 4 \int_{0}^{\dfrac{\pi}{2}}\sqrt{r^{2}sin^{2}\theta + r^{2}cos^{2}\theta }$

$L = 4 \int_{0}^{\dfrac{\pi}{2}}\sqrt{r^{2}(sin^{2}\theta + cos^{2}\theta)}$

$L = 4 \int_{0}^{\dfrac{\pi}{2}}\sqrt{r^{2}(1)}$

$L = 4 \int_{0}^{\dfrac{\pi}{2}}\sqrt{r^{2}}$

$L = 4 \int_{0}^{\dfrac{\pi}{2}} r$

$L = 4 [ r] _{0}^{\dfrac{\pi}{2}}$

$L = 4r \dfrac{\pi}{2}$

$L = 2\pi r$.

Why Is Circumference 2pir and Not Pid?

We usually use $2\pi r$ instead of $\pi d$ as a circle is usually given in terms of its radius rather than diameter. Note that the diameter $d$ is equal to twice the radius, i.e., $d=2r$, so we can write $2\pi r = \pi d$, and both formulas are equally valid.

2pir Calculator

To calculate the circumference, we need the value of $\pi$ and radius. We already know that the value of $\pi$ is given as $\dfrac{22}{7}$, while the value of the radius is either given or we calculate it if we are given the area of the circle.

If we are given the value of the diameter instead of the radius, we will first calculate the value of the radius by using the formula for the diameter of the circle $D =\dfrac{r}{2}$.

Applications of the Circumference of the Circle

Here are some real-life applications of the circumference of the circle:

This formula will be used whenever we encounter a circular shape in real life.
The wheel is considered to be one of the best inventions in human history. The circumference formula is essential in designing the model of a wheel.
The formula is used in solving different trigonometric problems, especially equations of the circle.
The hub of a ceiling fan has a circular shape, so we have to use this formula to calculate the perimeter of the hub.
Different forms of coins currency, buttons and circular clocks are all applications of the circle’s circumference, and we have to use this formula while designing all these stuff.
$2\pi r$ formula is also used in the calculation of the average speed of an object moving in a circular path. The formula to calculate the velocity of an object moving in a circular path is given as 2pir/t.

Example 1:

If the circle’s radius is 20 cm, what will be the circle’s circumference?

Solution:

Radius of the circle $= 20 cm$

Circumference of the circle $= 2.\pi.r$

C $= 2 \pi . 20$

C $= 125.6$ cm

Example 2:

If the circle’s diameter is 24cm, what will be the circle’s circumference?

Solution:

Diameter $= 24$

Radius of the circle $= \dfrac{24}{2} = 12$

Circumference of the circle $= 2.\pi.r$

$C = 2 \pi.12$

$C = 75.36 cm$

Example 3:

The perimeter of a square-shaped thread is $250 cm$. If the same thread is used to form a circle, what will be the circumference of the circle? You are also required to calculate the radius and diameter of the circle.

Solution:

We know that the perimeter of the square thread = the total amount of thread used to create the square. This will also be equal to the circumference of the circle because if we use the same thread to form the circle, the length of the circumference will remain the same.

Circumference of the circle $= 250$ cm

$C = 2.\pi.r$

$250 = 2\times \pi \times r$

$r = \dfrac{250}{\pi \times r}$

Example 4:

The difference between the circumference and diameter of a football is $10$ cm. What will be the radius of the football?

Solution:

Let the radius of the football $= r$

As given in the statement, circumference – diameter $= 10$ cm

Circumference of the football $= 2.\pi.r$

Diameter of the football $= 2.r$

$2. \pi . r – 2r = 10$

$r ( 2\pi – 2) = 10$

$r ( 4.28 ) = 10$

$r = \dfrac{10}{4.28} = 2.34$ cm approx.

Example 5:

A shepherd wants to build a circular boundary to keep his cattle safe from hounds and predators. What will be the total estimated cost if the $30$ meter radius of the circular boundary is charged at $\$15$ per meter?

Solution:

We will calculate the total length of the circular boundary and then multiply it with \$15.

Circumference of the boundary $= 2.\pi.r$

$C = 2 \times 3.14 \times 30$

$C = 188.4$ meter

Total cost of the circular boundary $= 188.4 m \times $15 \dfrac{1}{m} = \$2826$

2pir vs pi r^2

The main difference between these is that the circumference given as $2\pi r$ is the total length of the boundary of the circle, while the area enclosed by a circle of radius $r$ is given as $\pi r^2$. Many students confuse the circumference of the circle with the area of the circle and their corresponding formulas. Remember that circumference is a length and its units are measured in centimeters, meters, etc, while the units of area are meters-squared or centimeter-squared, etc.

Example 6:

Calculate the value of 2pir and $2\pi r^2$ if the area of the circle is $64 cm ^{2}$.

Solution:

The formula for area of the circle is given as:

Area of the circle $= \pi r^{2}$

$64 = 3.14 \times r^{2}$

$r^{2} = 20.38$

$r = 4.51 cm$ approx

$2.pi.r = 2 \times 3.14 \times 4.51 = 28.32$ cm approx.

$2.pi. r^{2} = 2 \times 3.14\times 20.38 = 128 cm^{2}$ approx

The value of 2pir and $2\pi r^2$ can be calculated using 2pir and 2pir^2 calculator as well.

Practice Questions:

The wheel of a car has a radius of $7$ meters. Ignoring friction and other factors, if the car’s wheel rotates once, what will be the distance covered by the vehicle?
Mr. Alex is working as a teacher in a school and he took his class to a summer camp near a forest. There was a huge tree near the camp house, and Mr. Alex promised the class a box of chocolates if they could calculate the tree’s diameter without using scale tape. The circumference of the tree is $48.6$ ft. Help the class determine the diameter of the tree.
A copper wire is bent to form a square shape. The area of the square is $100 cm^{2}$. If the same wire is bent to form a circle, what will be the circle’s radius?
Suppose the area of a circular track is $64 m^{2}$. What will be the circumference of the track?

Answer Key:

The radius of the wheel is $= 7 meters$

Distance covered during one rotation of wheel = circumference of the wheel

C $= 2.\pi.r$

$C = 2 \times 3.14 \times 7 = 43.96$ meters

Circumference of the tree $= 48.6$ ft

$C = 2.\pi.r$

$48.6 = 2 \times 3.14 \times r$

$48.6 = 6.38 \times r$

$r = \dfrac{48.6}{6.38} = 7.62 ft$

Diameter of the tree $= 2\times r = 2 \times 7.62 = 15.24$ ft.

All sides of the square are the same. Let us name all the sides as “a”.

Area of the square $= a^{2}$

Area of the square $= 100 cm^{2}$

$a^{2} = 100$

$a = 104$ cm

Perimeter of the square $= 4\times a = 4 \times 10 = 40 cm$.

If the same wire is used to form a circle, the overall length of the boundary or the surface remains the same. Hence, the circumference of the circle $= 40$ cm.

$C = 2.\pi.r$

$40 = 2.\pi.r$

$r = 6.37$ cm

Area of the circular track $= 64 m^{2}$

Formula for area of the circle $= \pi.r^{2}$

$r^{2} = \dfrac{113}{3.14} \cong 36$

$r = \sqrt{36}$

$r = 6$ meter

Circumference of the circular track $= 2.\pi.r$

$C = 2\pi\times 6 = 37.68$ meter