The Domain of ln(x): The Natural Logarithm

The domain of $\ln(x)$ is $x>0$, which means that $x$ can only accept positive real values. The natural logarithm, represented by $\ln x$, is the logarithm having the base $e$. This complete guide will teach you about natural logarithms, their domains, and ranges.

What Is the Domain of In (Natural Logarithm)?

The domain of $\ln(x)$ is $x>0$.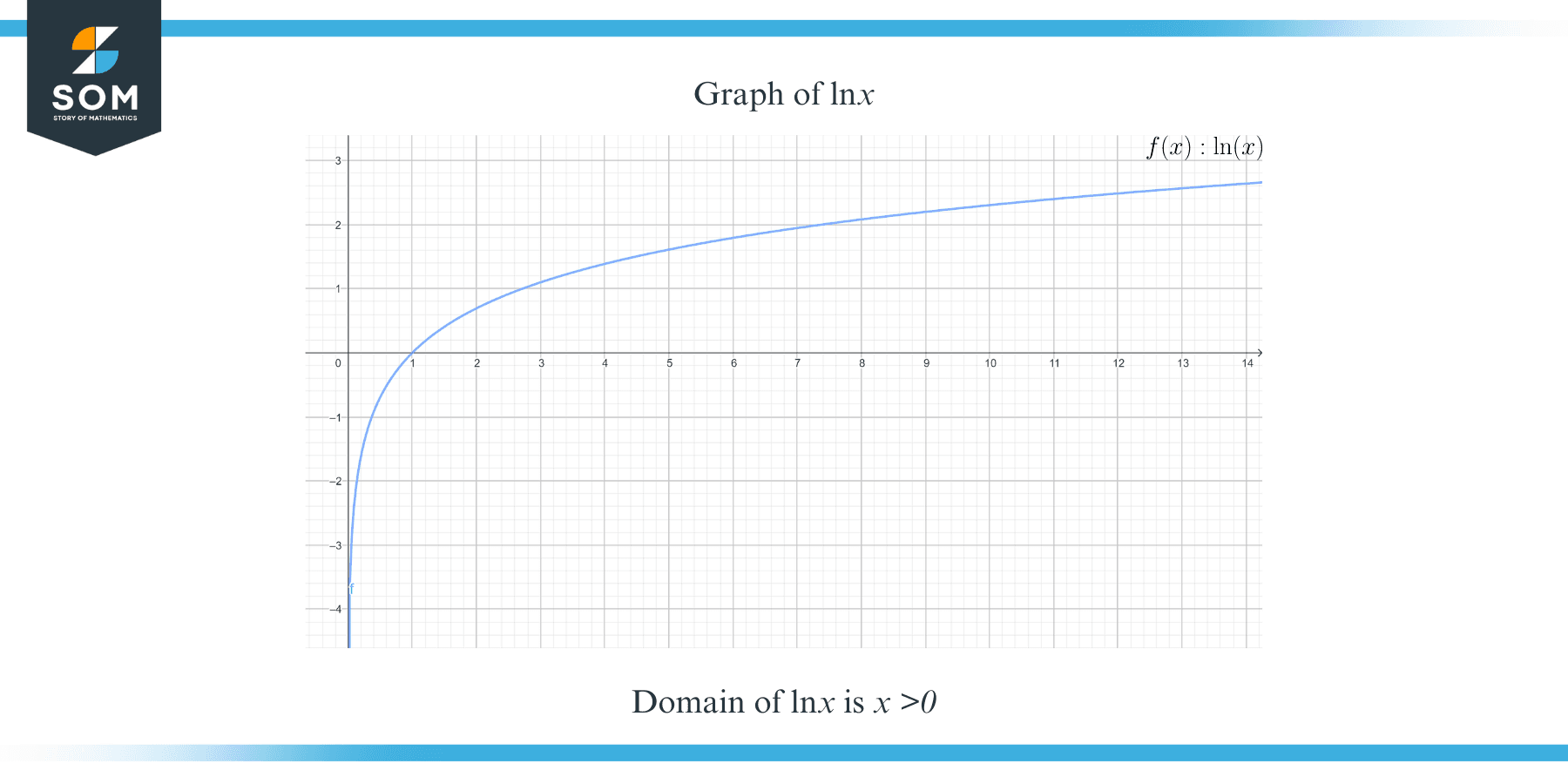

In mathematics, a domain is the collection of all values for which a function produces an outcome. The term is also utilized to define the set of all possible values for which a given equation holds. A domain of such a function is the collection of all real numbers. In other words, the domain of a logarithmic function is all real numbers except those with undefined results.

Range of the Natural Logarithm

A domain is the collection of all input values for which a function returns a value. A logarithmic function’s range is the collection of all positive real numbers. This function is a one-to-one function, which means that every input value yields a distinct output value. The logarithmic function is also an onto function, which means that it generates every possible output value.

Graph of the Logarithmic Function

The exponent in the exponential function is $x$ that is, the independent variable. The inverse of a function tells us the input value of the function when we already know the output value. Similarly, a logarithm will tell you the exponent. So, in simple words, a logarithm is an exponent.

One-to-one functions have the additional property of having inverses that are also functions. These functions can be used to solve equations on both sides. A horizontal line test is also passed by such functions.

A logarithmic function is the inverse of an exponential function. Recall that having switched the $x$ and $y$ coordinates yields the inverse of a function. This corresponds to the graph centered on the line $y=x$. The logarithmic curve is a representation of the exponential curve.

One-to-One Functions

Let $g$ be a function. If each element in the range of $g$ maps to exactly one element in the domain of $g$, you can say that $g$ is a one-to-one function. You can also write a one-to-one function as $1-1$.

A function $f(x)$ is a technique for relating the elements of one variable to the elements of some other variable such that the elements of the first variable result in the elements of the second variable similarly.

What Is the Domain of a Function?

The domain of a function is the entire set of independent variable values. In other words, the domain is the collection of all possible values of $x$ that will cause the function to work and produce real values of $y$.

When determining the domain, keep in mind that the denominator of a fraction can never be zero. The number underneath a square root symbol has to be positive.

Finding the Domain of a Function

In general, we find the domain of every function by searching for the independent variable values that we are permitted to use.  Normally, you must avoid using $0$ in the denominator of a fraction or negative values underneath the square root sign.

What Is the Range of a Function?

Once you have plugged in the domain, the range of a function is the entire set of all resulting values of the dependent variable. To put it simply, the range is the resulting $y$-values obtained upon substituting all possible $x-$values.

Finding the Range of a Function

A function’s range is the range of possible values of $y$, that is, from minimum values of $y$ to maximum values of $y$. To observe what happens, try various $x$-values in the expression for $y$.

Make a mental note of the maximum and minimum $y$ values. You can also make a sketch — a picture is worth a thousand words, as the saying goes.

What Is a Logarithm?

Logarithm is the value that represents the power to which the base number, which is fixed, is raised to determine a pre-given number.

Even though the fact that logarithms are accurately defined as reverse exponential operators in the true sense, it’s not the reason they were discovered. Logarithms were utilized as computation tables when John Napier initially published his finding regarding logarithms in 1614.

You can think of log tables as an even more enhanced form of multiplication tables. Logarithms have been used to reduce complex multiplication and division calculations to simple addition and subtraction. After all, this was before computers and calculators, when even simple multiplications took time. Nowadays, most of us do not use logarithmic tables.

Types of Logarithms

Logarithms are divided into two categories: common logarithms, and natural logarithms. While working with logarithms, the most common bases are base $e$ and base $10$.

The letter $e$ stands for an irrational number with numerous applications in science and mathematics. $e$ has the approximate value of $2.718…$. Log with the base $10$ is usually known as the common logarithm.

If you cannot see the base written with this logarithm, you will know already that the $\log$ is of the base $10$. Similarly, the $\ln$ is the notation to depict the natural log, that is, the logarithm to the base $e$.

Logarithm Applications

Logarithms have numerous practical applications. Logarithms are particularly useful for creating more controllable measurement scales. Instances of logarithmic applications include the Richter scale for quantifying earthquakes, the decibel scale for measuring sound, orders of magnitude, and data analysis.

What Is a Function?

A function is a law, rule, or expression that describes a relationship between a single variable known as the independent variable, and another variable known as the dependent variable.

Functions are common in mathematics and are required for the formulation of physical relationships in the sciences. A function is a relationship between inputs in which every input is associated to accurately one output. Each function has a domain as well as a co-domain, in addition to a range.

In a broad sense, a function is represented by $f(x)$, in which $x$ is the input. More generally,  a function can be defined as $y = f (x)$. In mathematics, there are various kinds of functions. Common types are One-to-one functions and Onto functions, in which there are multiple elements mapped from domain to range. There is also the polynomial function, where a function is made up of polynomials, and the inverse function, where a function can be used to invert another function.

Logarithmic Functions

The inverses of exponential functions are logarithmic functions, and therefore any exponential function could be represented in logarithmic form. The logarithmic functions can also be written in exponential form. Logarithms are extremely useful in allowing us to work with some very large numbers whilst also manipulating much smaller numbers.

Logarithmic functions are mathematical tools that can be utilized to determine the logarithm of a number. A number’s logarithm is the exponent to which a base should always be raised to generate that number.

Exponential Function

The exponential function is a mathematical function of the type $f(x) = a^x$, in which $x$ is a variable and $a$ is a constant that is termed as the function’s base and must be greater than $0$. The transcendental number $e$, which itself is approximately equivalent to $2.718…$, represents the most widely used exponential function base. The exponential curve is determined by the exponential function and the value of $x$.

Among the most significant functions in mathematics is the exponential function. The exponent of an exponential function is the independent variable. The exponential function grows rapidly, and exponential functions solve the most basic types of dynamical systems. In simple models of bacterial growth, for instance, an exponential function appears. An exponential function can be employed to identify the growth or decay.

The $\ln$ or a Natural Log

As previously suggested, the logarithm to the base $e$ is known as the natural logarithm and is symbolized by $\ln x$. The natural log is denoted by $\log_e (x)$. Its exponent form is $e^x =y$.

Logarithmic functions are utilized in mathematics and science to find solutions by transforming them into exponential equations. This enables much easier calculations to be used to work out solutions.

Conclusion

We have already covered logarithms, natural logarithms, and the domain and range of natural logarithms, so to gain a more thorough knowledge of the entire study, let us summarize this guide:

• The domain of $\ln(x)$ is $x>0$.
• The domain of a function is the entire set of independent values of the variable.
• After you have substituted the domain, the range of a function is the entire set of all resulting values of the dependent variable, usually named as $y$.
• Logarithmic functions are the inverses of exponential functions.
• The logarithm to the base $e$ is called the natural logarithm and is denoted by $\ln x$.

The simplest way to determine a function’s domain is to look up the values for which it is defined. Because negative values render the logarithm undefined, the natural logarithm is defined for all positive values of a variable and hence you can say that the domain of $\ln x$ is $x>0$. The convenient way to find the domain and range is to draw the graph of the given function, so why not draw a graph of $\ln x$ to better understand the domain of $\ln x$?