JUMP TO TOPIC

In the following article, we’ll explore the fundamental principles defining 3D rectangles, delve into their fascinating properties, and illustrate their indispensable roles in simple and complex structures around us.
Definition
A “3D rectangle” is more formally known as a rectangular prism or a cuboid in geometry. It is a three-dimensional solid shape bounded by six faces, all rectangles. The defining properties of a rectangular prism are:
- It has six faces, each of which is a rectangle.
- The opposite faces of the prism are identical.
- It has 12 edges and 8 vertices.
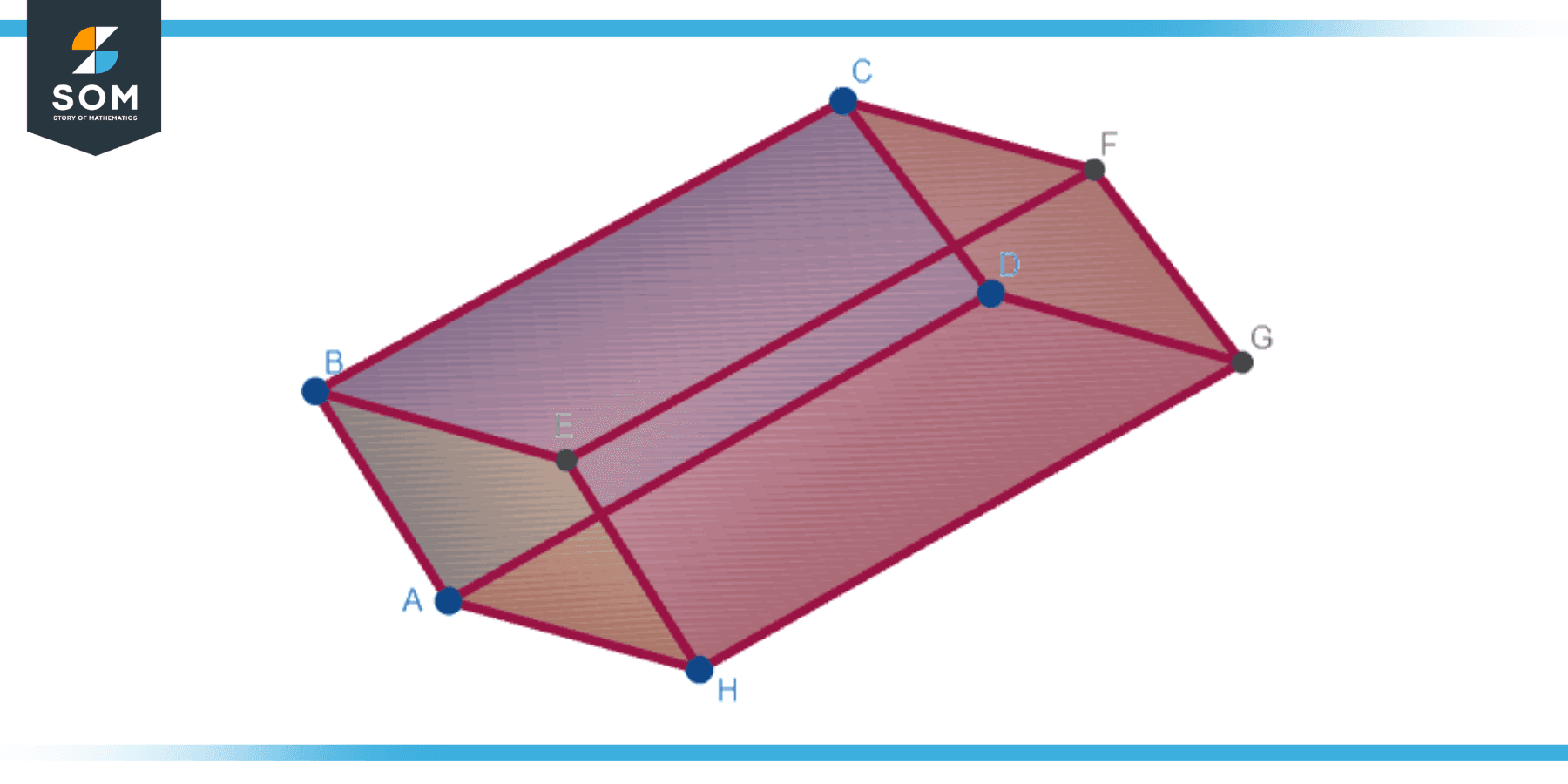
Figure-1.
The term “3D rectangle” isn’t often used in formal geometric contexts, but it’s typically understood to mean a rectangular prism or cuboid. This shape is common worldwide, seen in items like books, boxes, and buildings.
Ralevent Formulas
A 3D rectangle, or a rectangular prism (a cuboid), has several key formulas. Here are those formulas and their explanations:
Volume (V)
The volume of a rectangular prism can be calculated by multiplying the length (l), width (w), and height (h) of the prism. The formula is:
V = lwh
Surface Area (A)
The surface area of a rectangular prism is the sum of the areas of all six faces. Since opposite faces on a rectangular prism have the same area, this can be calculated by finding the area of each unique face (length x width, length x height, width x height), and then multiplying by 2:
A = 2lw + 2lh + 2wh
Space Diagonal (d)
The space diagonal of a rectangular prism is the line segment that passes through the interior of the prism, connecting two opposite corners (or vertices). This can be calculated using the three-dimensional version of the Pythagorean theorem:
d = sqrt(l² + w² + h²)
The perimeter of Base (P)
The perimeter of the base of a rectangular prism (if considering one of the rectangular faces as a base) can be found by adding up all the sides of the rectangle (which is 2 times the sum of the length and the width):
P = 2l + 2w
Lateral Surface Area (LA)
The lateral surface area of a rectangular prism is the area of the four faces not considered the base or top. It can be found by multiplying the perimeter of the base by the height:
LA = Ph = 2lh + 2wh
Exercise
Example 1
Suppose a 3D rectangle has a length of 5 cm, a width of 4 cm, and a height of 3 cm. What is its volume?
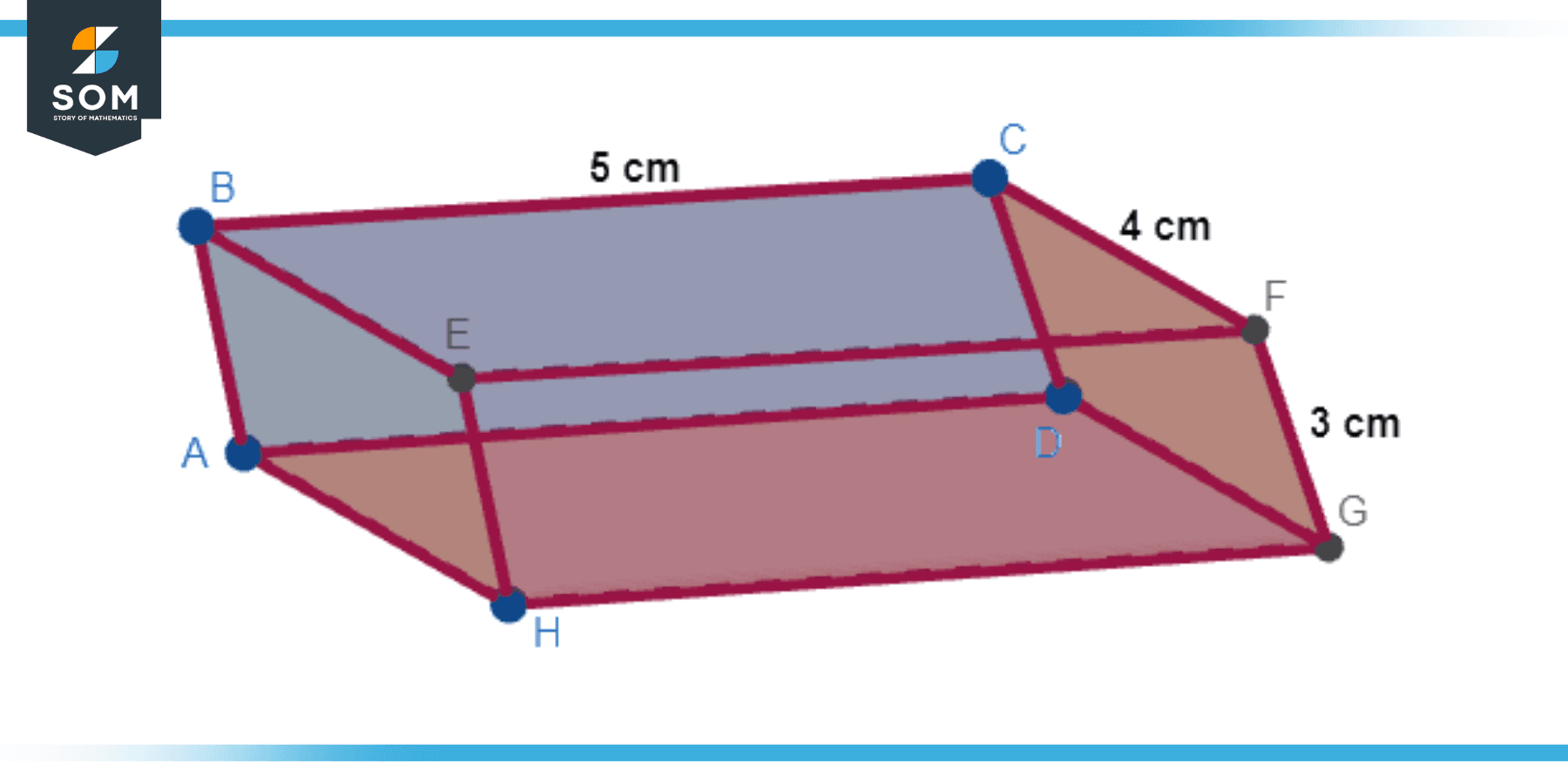
Figure-2.
Solution
The volume can be computed as follows:
Volume = length x width x height
Volume = 5 cm x 4 cm x 3 cm
Volume = 60 cubic cm.
Example 2
Suppose a 3D rectangle has a length of 7 m, a width of 3 m, and a height of 6 m. What is its surface area?
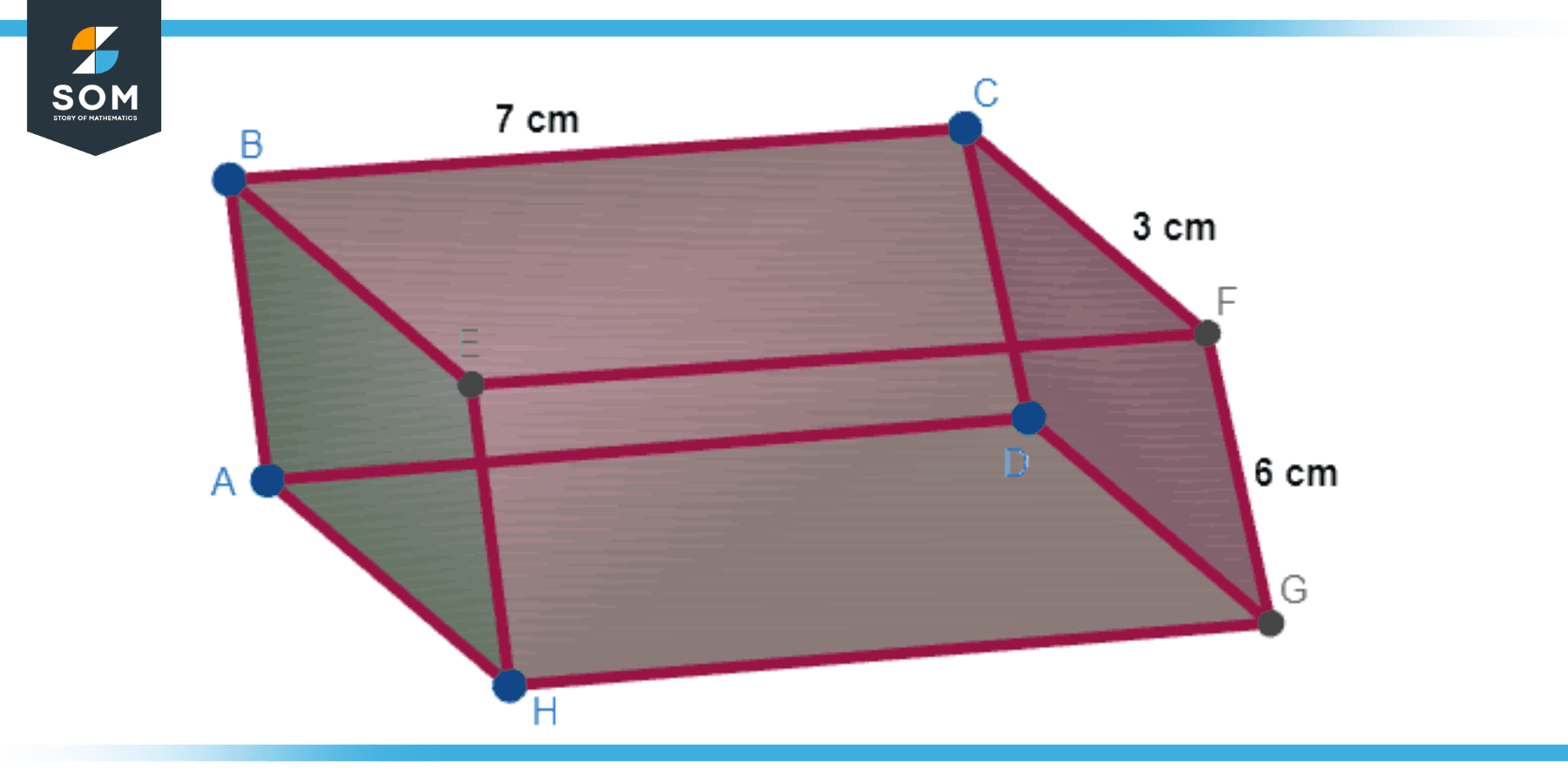
Figure-3.
Solution
Surface Area = 2lw + 2lh + 2wh
Surface Area = 2(7 m x 3 m) + 2(7 m x 6 m) + 2(3 m x 6 m)
Surface Area = 42 m² + 84 m² + 36 m²
Surface Area = 162 square m
Example 3
Suppose a 3D rectangle has a length of 8 m, a width of 5 m, and a height of 4 m. What is the length of its space diagonal?
Solution
Space Diagonal = sqrt(l² + w² + h²)
Space Diagonal = sqrt((8 m)² + (5 m)² + (4 m)²)
Space Diagonal = sqrt(64 m² + 25 m² + 16 m²)
Space Diagonal = sqrt(105 m²)
Space Diagonal = 10.25 m
Example 4
Suppose a 3D rectangle has a length of 8 cm and a width of 5 cm. What is the perimeter of its base?
Solution
Perimeter = 2l + 2w
Perimeter = 2(8 cm) + 2(5 cm)
Perimeter = 16 cm + 10 cm
Perimeter = 26 cm
Example 5
Suppose a rectangular prism has a length of 7 m, a width of 3 m, and a height of 4 m. What is its lateral surface area?
Solution
Lateral Surface Area = 2lh + 2wh
Lateral Surface Area = 2(7 m x 4 m) + 2(3 m x 4 m)
Lateral Surface Area = 56 m² + 24 m²
Lateral Surface Area = 80 square m
Applications
Mathematics and Physics
Rectangular prisms are foundational in understanding three-dimensional space and concepts like volume and surface area. They are often used in problem-solving and mathematical proofs. In physics, they can represent objects in kinematics problems or even areas of space in field problems.
Engineering and Architecture
Rectangular prisms are a common shape in buildings and engineered products, thanks to their stability and ease of construction. Architects use them to model rooms and buildings, while engineers might design anything from a small tool to a large machine. Understanding the properties of a rectangular prism is crucial for determining load capacities, space utilization, and structural integrity.
Computer Graphics and Gaming
In 3D modeling and computer graphics, complex shapes are often broken into small rectangular prisms (or cuboids) to simplify rendering. This is particularly true in voxel-based games like Minecraft, where the world comprises many small cubes, a type of rectangular prism.
Logistics and Shipping
Rectangular prisms are the most common shape for boxes and shipping containers. Understanding these prisms’ properties helps optimize packing and stacking arrangements, maximizing the use of space and potentially saving significant costs.
Geology and Geophysics
In disciplines like geology and geophysics, rectangular prisms can represent rock or soil volumes in models of the Earth’s crust. This is particularly useful in fields like resource exploration or seismic analysis, where understanding the properties of different volumes of earth is important.
All images were created with GeoGebra.
