JUMP TO TOPIC
by William Smith

The cos 45 degrees, symbolized as cos(45°) holds a special place in the fascinating world of trigonometry, we encounter key concepts related to cos(45°) that serve as the foundation of this mathematical discipline. The cosine of an angle is a fundamental measure that plays a vital role in many mathematical and physical phenomena.
This discussion focuses on a specific, highly significant angle: 45 degrees. The cosine of 45 degrees, symbolized as cos(45°), carries an intriguing property of equanimity due to its equidistant position on the unit circle and is deeply embedded in various mathematical applications.
From geometry to physics, the value of cos(45°) opens the door to a profound understanding of our universe, driving advancements in fields as diverse as architecture, computer science, and engineering. Below we present a generic diagram for all angles.
Figure-1.
This article will delve into the unique aspects of cos(45°), unfolding its mathematical beauty and real-world significance.
Definition of cos 45 Degrees
In trigonometry, the cosine of an angle in a right triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. When we talk about an angle of 45 degrees, we’re referring to an angle that’s halfway between 0 and 90 degrees. Below we present a generic diagram for the cosine 45 degrees.
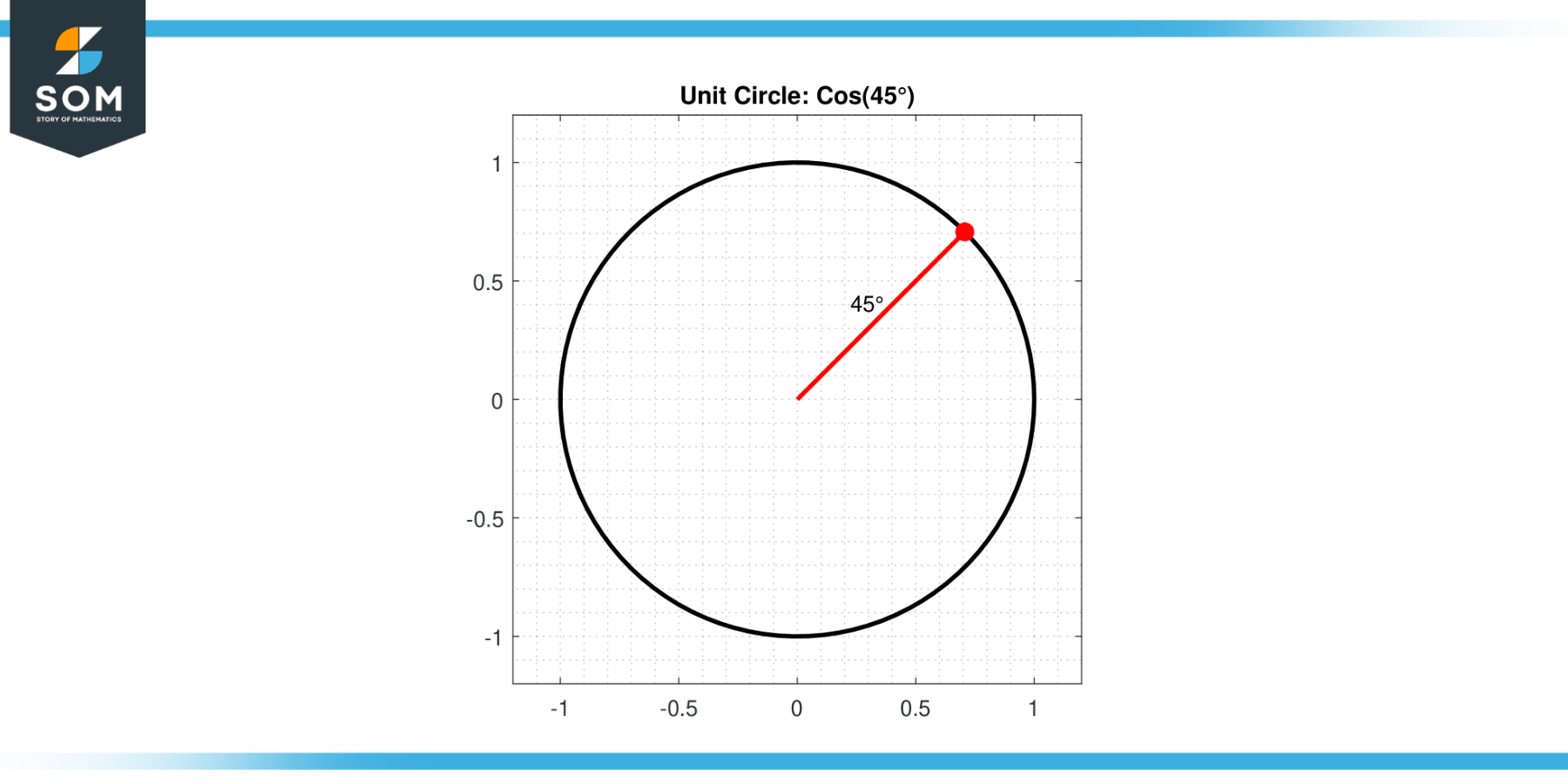
Figure-2.
The cosine of 45 degrees holds a special property due to the symmetry of a 45-45-90 triangle. In this type of triangle, the two non-right angles are 45 degrees, and the sides opposite these angles are of equal length. Given this equality and the Pythagorean theorem, we can conclude that the cosine of 45 degrees is equal to √2 / 2, or approximately 0.7071.
It’s important to note that this value is derived based on the unit circle definition, often used in trigonometry. In the unit circle, the cosine of an angle is the x-coordinate of the point on the circle corresponding to that angle. In the case of 45 degrees, or π/4 radians, this coordinate is √2 / 2. Below we present a generic diagram for the cosine 45 degrees along with the segment of a cosine function.
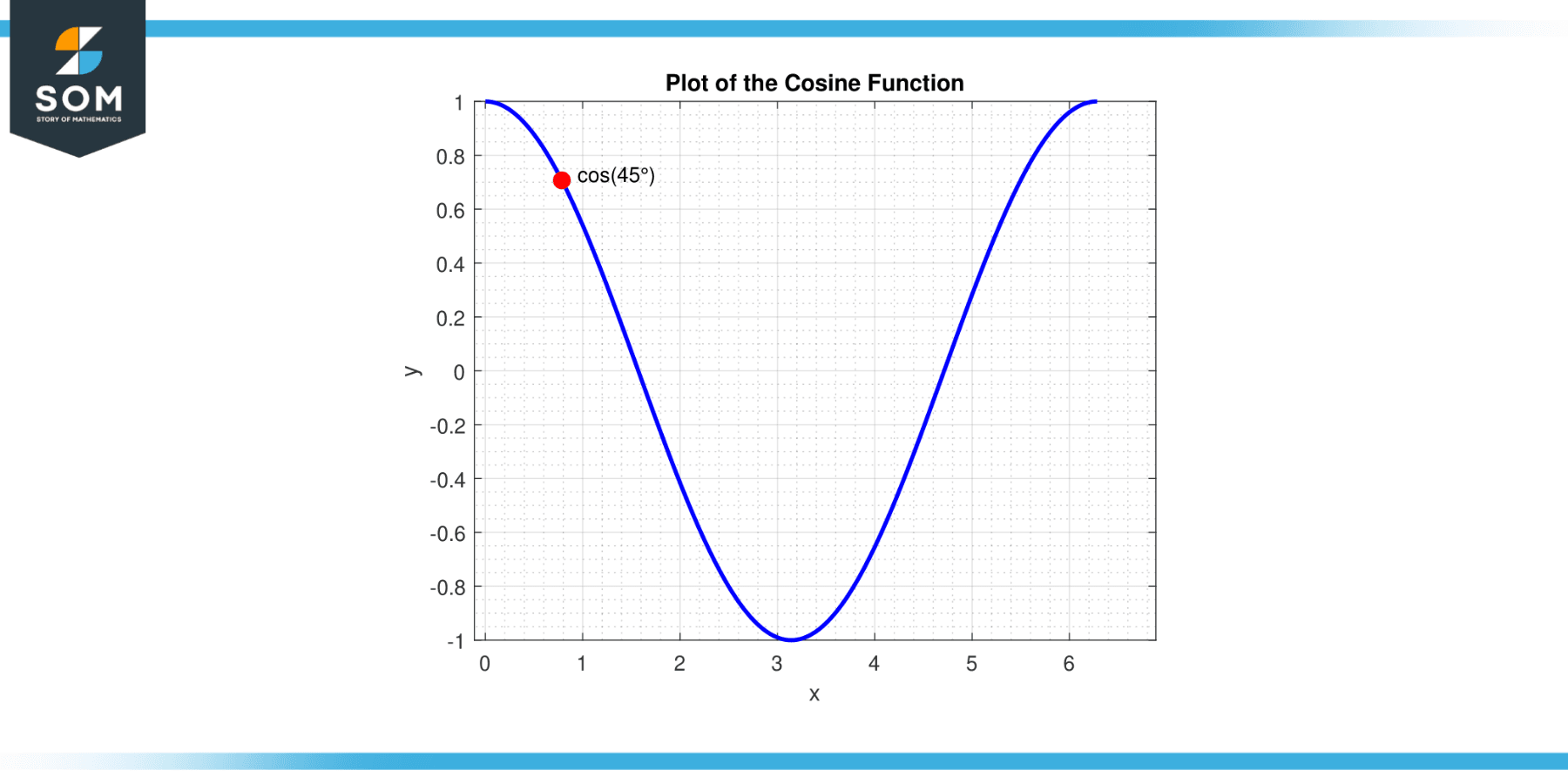
Figure-3.
Significance of Cos(45°) In Trigonometry
The cosine of 45 degrees is a key value in trigonometry due to its unique and elegant properties. Its value, √2 / 2, holds a profound place in the study of mathematics for several reasons:
Special Right Triangles
The 45-45-90 triangle, also known as an isosceles right triangle, is one of the two types of special right triangles. Because the two non-right angles are both 45 degrees, and the sides opposite these angles are of equal length, cos(45°) is the ratio of the length of either leg to the length of the hypotenuse. Thus, the concept of cos(45°) is fundamental in the study of these special right triangles.
Unit Circle
In the context of the unit circle, which is a central tool in trigonometry, the cosine of an angle is defined as the x-coordinate of the point where the terminal side of the angle intersects the unit circle. For an angle of 45 degrees, this x-coordinate is √2 / 2, once again demonstrating the significance of cos(45°).
Symmetry
The value of cos(45°) is a beautiful demonstration of the symmetry inherent in trigonometry. In a 45-45-90 triangle, the cosine and sine of the 45-degree angle are equal (√2 / 2), highlighting the complementary nature of these two fundamental trigonometric functions.
Complex Numbers and Euler’s Formula
The cos(45°) also plays a crucial role in the field of complex numbers, specifically in Euler’s formula, which states that e^(ix) = cos(x) + i*sin(x). At x = 45 degrees or π/4 radians, both cosine and sine equal √2 / 2, simplifying many calculations in this complex plane.
Real-World Applications
Beyond pure mathematics, cos(45°) is crucial in various applied fields, including physics, engineering, computer science, and more. For example, it’s essential in calculating angles of projection for maximum range, analyzing waves and oscillations, interpreting rotation matrices in computer graphics, and much more.
Hence, the importance of cos(45°) in trigonometry and beyond is undeniable. Its mathematical elegance and widespread applicability makes it a cornerstone of mathematical understanding.
Properties of cos 45 Degrees
The cosine of 45 degrees, denoted as cos(45°), exhibits some intriguing properties in trigonometry. Let’s delve into them:
Value
The value of cos(45°) is √2/2, approximately equal to 0.7071. This is derived from the geometry of the 45-45-90 right triangle or by using the unit circle definition of the cosine function.
Symmetry
One of the fascinating properties of cos(45°) is its symmetry with respect to the sine function. Specifically, sin(45°) = cos(45°), which is a manifestation of the complementary nature of these two functions. This is due to the fact that in a 45-45-90 triangle, the two legs are of equal length.
Periodicity
The cosine function is periodic with a period of 360° or 2π radians. Therefore, cos(45° + n*360°) = cos(45°) for any integer n. This property highlights the repeating nature of the cosine function.
Even Function
Cosine is an even function, which means that cos(x) = cos(-x) for any angle x. Therefore, cos(45°) = cos(-45°), underscoring the function’s symmetry about the y-axis.
Cosine-Square Identity
Using the Pythagorean identity in trigonometry, we know that sin²x + cos²x = 1 for any angle x. Substituting x with 45°, we see that the square of cos(45°) is 1/2. This is a direct application of the cosine function to the fundamental identity.
Double Angle Identity
The double angle identity for cosine can be used to find cos(90°) using cos(45°). According to the formula, cos(2x) = 2cos²x – 1, therefore, cos(90°) = 2cos²(45°) – 1 = 0.
These properties not only elucidate the nature of the cosine function and its inherent relationships within trigonometry but also facilitate problem-solving across a wide range of mathematical contexts.
Techniques for Constructing and Measuring a Cos(45°) Degree Angle
Constructing and measuring a 45-degree angle, specifically relating to cos(45°), requires some basic knowledge of geometry. Here are some steps and techniques:
Constructing a 45-Degree Angle Using a Compass and Straightedge
Draw a Base Line
Using a straightedge, draw a straight line. This line will serve as the base or arm of your angle.
Construct a Perpendicular Line
From a point on this line, use a compass to draw an arc intersecting the line. Then, without changing the compass width, draw another arc above the line using the intersection point as the center. Draw a line through the two arc intersections; you now have a 90-degree angle.
Bisect the 90-Degree Angle
To bisect an angle means to divide it into two equal parts. Keep the same width on the compass, and draw an arc cutting both arms at a 90-degree angle. Draw two more arcs within the angle without changing the width using the intersections on the arms as centers. Draw a line from the angle’s vertex through the intersection of these two arcs, and you have now bisected the 90-degree angle into two 45-degree angles.
Measuring a 45-Degree Angle Using a Protractor
Position the Protractor
Place the center of the protractor at the vertex of the angle. Ensure the angle’s baseline aligns with the protractor’s zero line.
Read the Measurement
The second line of the angle will pass through the 45-degree mark on the protractor if it’s a 45-degree angle.
Using Trigonometry
The value of cos(45°) can also be confirmed using trigonometry. In a right triangle, if the lengths of the two legs are equal, the non-right angles are both 45 degrees. If you construct such a triangle and measure the ratio of the length of one leg to the length of the hypotenuse, it should be equal to cos(45°), which is √2/2, or approximately 0.7071.
These techniques are helpful in various fields, from mathematics and physics to engineering and design, where the construction and measurement of precise angles are often necessary. Below we present a generic diagram for the cosine 45 degrees constructed in MATLAB.
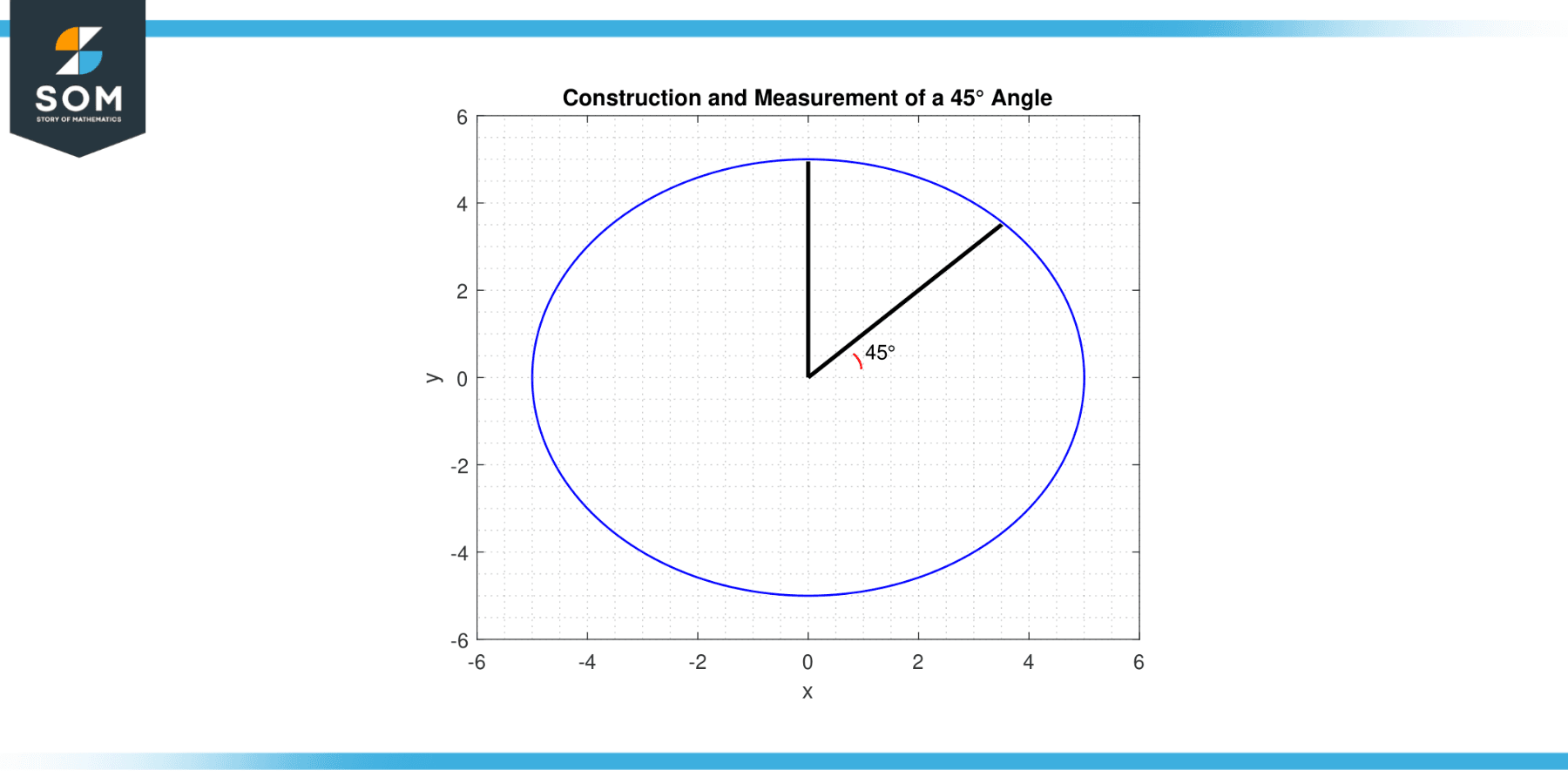
Figure-4.
Applications
The value of cos(45°) is instrumental in various fields due to its unique and symmetrical properties. It plays a pivotal role in several mathematical and physical applications.
Physics
In Projectile Motion, the maximum horizontal distance (range) a projectile can travel is achieved when it is launched at an angle of 45 degrees. This is because the cosine and sine of 45 degrees are equal (cos(45°) = sin(45°)), maximizing the formula for range, R = (v² sin(2θ))/g, where v is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity.
Engineering
In Structural Engineering, the force components are often analyzed in different directions. If a force is applied diagonally, the horizontal and vertical components of that force will be equal when the angle is 45 degrees, as cos(45°) = sin(45°). This principle is extensively used in analyzing trusses, bridges, and other structures.
Computer Science
In Computer Graphics, rotation matrices often use cos(45°) when rotating objects around the origin by 45 degrees. Similarly, cos(45°) is used in algorithms related to Image Processing and Machine Learning where rotation of images or data points in multi-dimensional space is required.
Mathematics
In Geometry and Trigonometry, cos(45°) is essential in solving problems related to right triangles, circles, and more. Its equality with sin(45°) is often leveraged to simplify calculations. Also, in Complex Numbers, cos(45°) appears in Euler’s formula, helping to link trigonometry and exponential functions.
Navigation and GPS
The concept of cos(45°) is used in GPS Technology for triangulating positions. When satellites are at 45 degrees to each other from the viewpoint of the receiver, the accuracy of the position fix is optimized due to the symmetry that cos(45°) provides.
Telecommunications
In Signal Processing, the Fourier Transform, a method for transforming a signal from the time domain to the frequency domain, leverages the cosine function. Signals can be decomposed into a sum of cosine and sine waves, and the cos(45°) may appear in calculations involving phase shifts or rotations in the signal.
Each of these applications underscores the profound impact of the seemingly simple trigonometric value, cos(45°), extending far beyond pure mathematics.
Exercise
Example 1
For the given equation, solve for x: cos(x) = cos(45°)
Solution
Given that cos(45°) = √2/2, we’re looking for angles x where cos(x) = √2/2.
Since the cosine function is periodic with a period of 360° or 2π radians, there are infinite solutions. However, the principal solutions in the range of 0 to 360 degrees are:
x = 45°
and:
x = 360° – 45°
x = 315°
Consequently, the solutions are x = 45° and x = 315°.
Example 2
Find the length of the diagonal d of a square with side length s.
Solution
In a square, the diagonal splits the square into two 45-45-90 triangles. Therefore, we can use this triangle’s property that the hypotenuse length (the diagonal in this case) is √2 times the length of a leg (the side of the square).
So, if we let s be the square’s side length, the diagonal d’s length is given by d = s√2.
To see how cos(45°) comes into play, recall that in a 45-45-90 triangle, cos(45°) = adjacent/hypotenuse. If we let the side of the square be the adjacent side, then cos(45°) = s/d.
Substituting the known value of cos(45°) = √2/2, we get:
√2/2 = s/d
Solving this equation for d gives us:
d = s√2
as before.
Example 3
If a force F acts at an angle of 45 degrees to the horizontal, find the horizontal component of the force.
Solution
The horizontal component Fx of a force F acting at an angle θ to the horizontal is given by:
Fx = Fcos(θ)
If θ = 45°, then we get:
Fx = Fcos(45°)
Given that cos(45°) = √2/2, the horizontal component of the force is:
Fx = F(√2/2)
which simplifies to:
Fx = F√2 / 2
Consequently, the horizontal component of the force is F√2 / 2.
All figures are generated using MATLAB.
