Use a double integral to find the area of the region. The region inside the cardioid r = 1 + cos(θ) and outside the circle r = 3 cos(θ).

This question aims to find the area of the region described by the given equations in polar form. 

A two-dimensional plane with a curve whose shape is like a heart is said to be a cardioid. This term is derived from a Greek word that means “heart.” Therefore, it is known as a heart-shaped curve. The graph of the cardioids is usually vertical or horizontal, that is, it depends upon the axis of symmetry but it can be in any orientation. This shape typically consists of two sides. One side is round in shape and the second has two curves meeting at an angle known as a cusp.

Polar equations can be used to illustrate the cardioids. It is well known that the Cartesian coordinate system has a substitute in the form of a polar coordinate system. The polar system has the coordinates in the form of $(r,\theta )$, where $r$ represents the distance from the origin to the point and the angle between the positive $x-$axis  and the line which connects the origin to the point is measured anti-clockwise by $\theta$. Usually, the cardioid is represented in the polar coordinates. Although, the equation which represents the cardioid in the polar form can be converted into Cartesian form.

Expert Answer

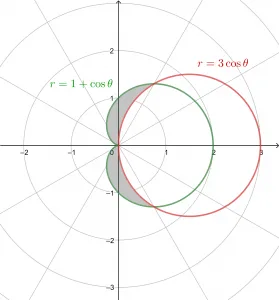
The required area of the region is shaded in the figure above. First, find the points of intersection in the first quadrant as:

$1+\cos \theta =3\cos \theta$

$2\cos \theta =1$

$\cos \theta ={\displaystyle \frac{1}{2}}$

$\theta ={\cos }^{-1}\left({\displaystyle \frac{1}{2}}\right)$

$\theta ={\displaystyle \frac{\pi }{3}},{\displaystyle \frac{5\pi }{3}}$

Since the point of intersection is in the first quadrant, therefore:

$\theta ={\displaystyle \frac{\pi }{3}}$

Let $D_1$ and $D_2$ be the regions defined as:

$D_1=\{(r,\theta ),3\cos \theta \le r\le 1+\cos \theta ,{\displaystyle \frac{\pi }{3}}\le \theta \le {\displaystyle \frac{\pi }{2}}\}$

$D_2=\{(r,\theta ),0\le r\le 1+\cos \theta ,{\displaystyle \frac{\pi }{2}}\le \theta \le \pi \}$

Since the area is divided into two portions. Let $A_1$ be the area of first region and $A_2$ be the area of the second region then:

$A_1=\underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}\underset{3\cos \theta }{\overset{1+\cos \theta }{\int }}rdrd\theta$

$=\underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\left|{\displaystyle \frac{r^2}{2}}\right|}_{3\cos \theta }^{1+\cos \theta }d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}[(1+\cos \theta {)}^2-(3\cos \theta {)}^2]d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}[1+2\cos \theta -8{\cos }^2\theta ]d\theta$

Since, ${\cos }^2\theta ={\displaystyle \frac{1+\cos 2\theta }{2}}$, therefore:

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}[-3+2\cos \theta -4\cos 2\theta ]d\theta$

$={\displaystyle \frac{1}{2}}{[-3\theta +2\sin \theta -2\sin 2\theta ]}_{\frac{\pi }{3}}^{\frac{\pi }{2}}$

$=1-{\displaystyle \frac{\pi }{4}}$

Also,

$A_2=\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}\underset{0}{\overset{1+\cos \theta }{\int }}rdrd\theta$

$=\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}{\left|{\displaystyle \frac{r^2}{2}}\right|}_0^{1+\cos \theta }d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}[(1+\cos \theta {)}^2-(0{)}^2]d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}[1+2\cos \theta +{\cos }^2\theta ]d\theta$

Since, ${\cos }^2\theta ={\displaystyle \frac{1+\cos 2\theta }{2}}$, therefore:

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}[{\displaystyle \frac{3}{2}}+2\cos \theta +{\displaystyle \frac{\cos 2\theta }{2}}]d\theta$

$={\displaystyle \frac{1}{2}}{[{\displaystyle \frac{3}{2}}\theta +2\sin \theta +{\displaystyle \frac{\sin 2\theta }{4}}]}_{\frac{\pi }{2}}^{\pi }$

$={\displaystyle \frac{3\pi }{8}}-1$

Since the region is symmetric with respect to $x$-axis, therefore, the total area of the required region is:

$A=2(A_1+A_2)$

$A=2(1-{\displaystyle \frac{\pi }{4}}+{\displaystyle \frac{3\pi }{8}}-1)$

$A={\displaystyle \frac{\pi }{4}}$

Example

Calculate the area inside the circle $r=2\sin \theta$ and outside the cardioid $r=1+\sin \theta$.

Solution

For the points of intersection:

$1+\sin \theta =2\sin \theta$

$\sin \theta =1$

$\theta ={\sin }^{-1}\left({\displaystyle \frac{1}{2}}\right)$

$\theta ={\displaystyle \frac{\pi }{6}},{\displaystyle \frac{5\pi }{6}}$

Now, let $A$ be the required area then:

$A={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{6}}{\overset{\frac{5\pi }{6}}{\int }}[(1+\sin \theta {)}^2-(2\sin \theta {)}^2]d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{6}}{\overset{\frac{5\pi }{6}}{\int }}[1+2\sin \theta -3{\sin }^2\theta ]d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{6}}{\overset{\frac{5\pi }{6}}{\int }}[1+2\sin \theta -3\left({\displaystyle \frac{1-\cos 2\theta }{2}}\right)]d\theta$

$={\displaystyle \frac{1}{2}}\underset{\frac{\pi }{6}}{\overset{\frac{5\pi }{6}}{\int }}[-{\displaystyle \frac{1}{2}}+2\sin \theta +{\displaystyle \frac{3\cos 2\theta }{2}}]d\theta$

$={\displaystyle \frac{1}{2}}{[-{\displaystyle \frac{1}{2}}\theta -2\cos \theta +{\displaystyle \frac{3\sin 2\theta }{4}}]}_{\frac{\pi }{6}}^{\frac{5\pi }{6}}$

$={\displaystyle \frac{1}{2}}[-{\displaystyle \frac{5\pi }{12}}+{\displaystyle \frac{5\sqrt{3}}{8}}+{\displaystyle \frac{\pi }{12}}+{\displaystyle \frac{5\sqrt{3}}{8}}]$

$={\displaystyle \frac{1}{2}}[-{\displaystyle \frac{\pi }{3}}+{\displaystyle \frac{5\sqrt{3}}{4}}]$

Hence, the required area is:

$A={\displaystyle \frac{5\sqrt{3}}{8}}-{\displaystyle \frac{\pi }{6}}$

Previous Question < > Next Question