Absolute Value of -8: A Detailed Explanation With Examples

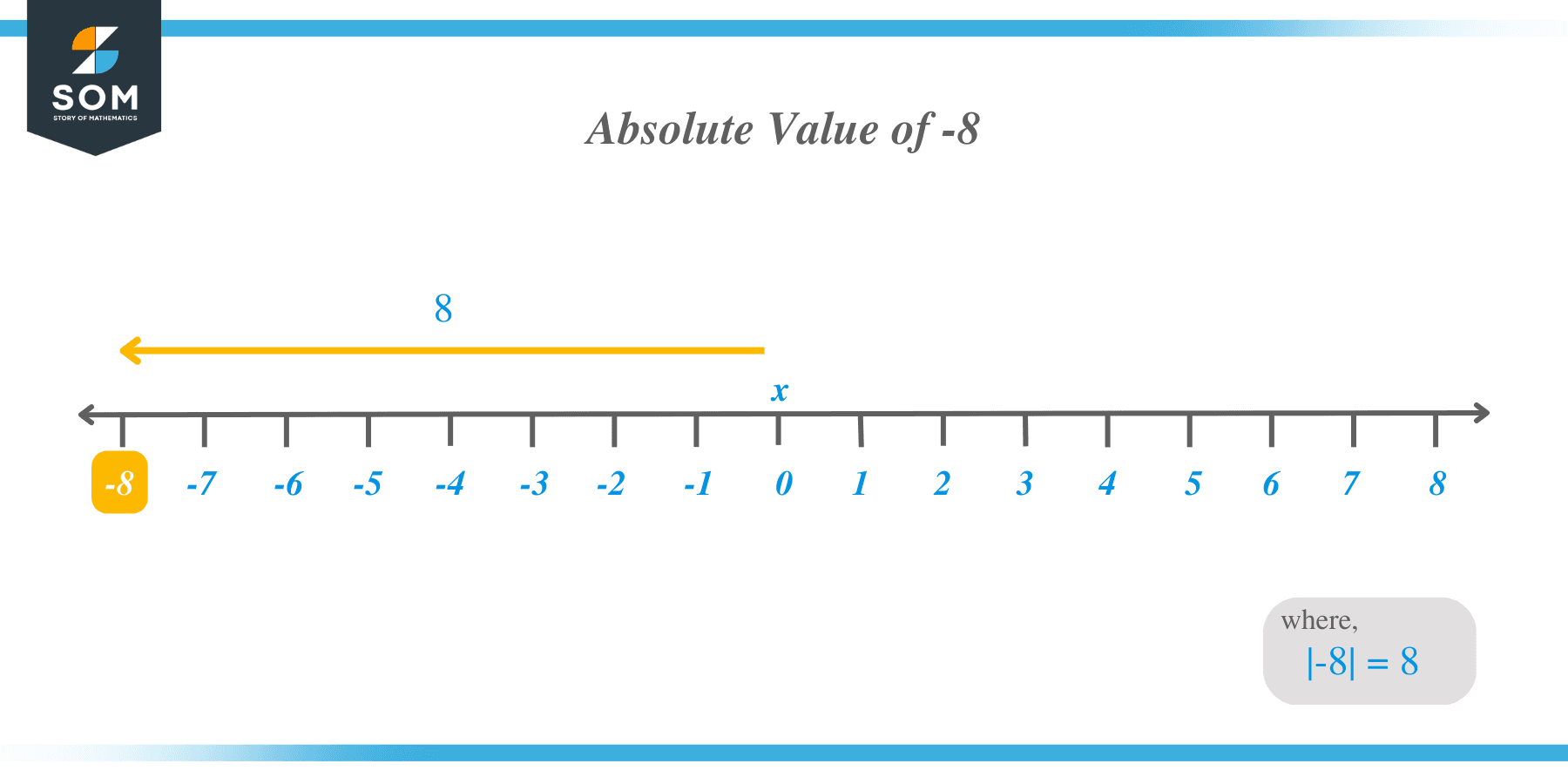
The absolute value of $-8$ is $8$.

The absolute value of any number is represented as | |. For example, we will represent the absolute value of $-8$ as $|-8|$, and the answer would be equal to $8$. The absolute value of $|8|$ is also $8$, hence the absolute value of $|-8|$ = $|8$| = $8$.

In this complete guide, we describe the concept of the absolute value, its significance, and its relation with the concept of the magnitude of a number.

Why Is 8 the Absolute Value of -8?

The absolute value of the number $-8$ is $8$ because the absolute value is the magnitude of the number and is always positive.

The Magnitude of a Number

The absolute value of a number is called the magnitude of that number. For example, if you are given a number $-8$, then the absolute value or modulus of $-8$ is always $8$, and that answer $8$ is the magnitude of the number $-8$. We know that the magnitude of any measurement is always positive.

The modulus or absolute value of any given quantity is also called the magnitude of that quantity. The magnitude of any variable quantity is always positive irrespective of its direction.

When dealing with vector quantities where a sign shows the direction of the vector and similarly other quantities like volume, price, etc, it is important to assign the sign to the values, but whenever we are required to calculate their absolute values or the magnitude, we ignore the negative sign.

So we can say that the magnitude of measurement is the absolute value of that measurement. Let us look at some examples so you can understand them easily.

Example 1:

Allan got pneumonia, and due to this disease, his weight decreased from $100$ pounds to $90$ pounds. The weight change during this disease is $-10$ pounds. How much weight did Allan lose?

Solution:

Allan lost $10$ pounds of weight in total, but do we say Allan lost $-10$ pounds? No, the answer is that Allan lost $10$ pounds of weight and not $-10$, and we calculate the magnitude of the weight using absolute. So by using absolute value of $-10$, we know that $| -10| = 10$.

Example 2:

Tania borrowed $\$100$ from Natalia. How much is Tania’s debt?

Solution:

In terms of finance, debt is always negated from the capital amount, so the debt of Tania is $\$-100$ as it will be subtracted from her capital or principal amount. Still, when someone asks Tania how much she owes Natalia, the answer will always be $\S100$. We take the absolute value of the amount she borrowed, so $|-100| = 100$.

Example 3:

Malen, Miller, and Mia went to the bank for a transaction. Malen deposited $\$100$. Miller made a withdrawal of $\$50$, and Mia credited $\$1000$ in her account. Who made the biggest transaction in terms of size using the concept of absolute value?

Solution:

We know that size cannot be negative, so we have to take the magnitude value of the transaction, and we can only do that by using the absolute symbol.

Malen deposited $\$100$, so his account has been added $100$ dollars, Miller withdraws $50$ dollars, so $50$ dollars was subtracted from his account, and finally, Mia credited $1,000$ dollars to her account (this means that she added or deposited $1,000$ dollars to her account).

The absolute value of Malen’s transaction is = $|100| = 100$

The absolute value of Miller’s transaction is = $|-50| = 50$.

The absolute value of Mia’s transaction is = $|1000| = 1000$.

So in terms of size, Mia made the biggest transaction.

Distance From Origin

The absolute value of any number is its distance from the origin or zero, and as we discussed earlier, distance is always taken as positive. In some quantities, assigning a positive or negative sign to a numeric value is important as it conveys important information about the quantity under discussion.

For example, a sign can indicate whether there is a percentage increase or decrease in shares or an increase or decrease in profits. However, when we want to disregard the sign, we take the modulus of the numeric value. In short, no sign is assigned to absolute values; hence the absolute value of $-8$ is taken as $8$.

Let us look at the example of light poles in the street. The distance between two poles is the value that tells us how far apart they are. Let us consider a coordinate system where one pole is at the origin and has several poles on its left and right sides.

Since we have poles on both left and right, we will arbitrarily assign positive values to one side and negative values to the other. Let’s say that the poles on the right side are on the positive axis with respect to the origin, and the ones on the left side are on the negative axis.

Now let’s take two arbitrary poles. If one pole is at the origin, then the distance of another pole from the first pole is the absolute value of its location in the coordinate system. Suppose if one pole is at origin or the location marked as 0 while the other pole is at location number $6$ on the right side, then the distance between them is taken as $|6|$.

Suppose there is a pole on the left side at location $6$, and we want to calculate the distance. Again using the absolute value, we can write $|-6| = 6$. In short, irrespective of the direction, both the poles will always be $6$ units away from each other.

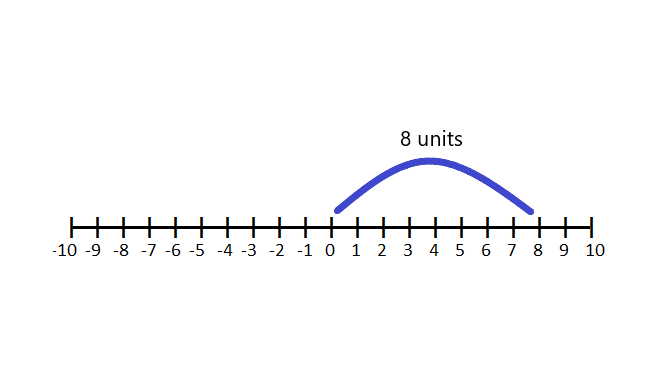
Now coming back to our original question, let us take the distance of “$8$” and “$-8$” from the origin. The distance of the number “$8$” from the origin is shown as $|8-0| = |8| = 8$.

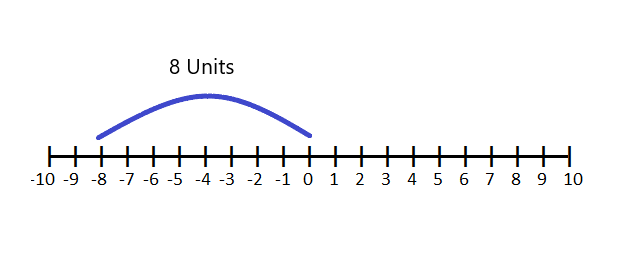
Similarly, the distance of “$-8$” from zero can be written as $|-8 -0| = |-8| = 8$. 

What |-8| Means

The absolute value of any number or a variable is represented by the number or variable inside the two vertical parallel lines. For example, the absolute value of the variable “$y$” will be represented as $|y|$, where y is an integer or real number and the answer of $|y| = y$.

Similarly,  the absolute value of $-8$ is written as $|-8|$, we will write the absolute value of $8$ as $|8|$, and the answer to both of these absolute values will be $8$ as in the case of absolute numbers we are only concerned with the magnitude of a quantity.

The quantity’s direction is not important, so the answer will always be a positive number. Hence, we conclude that we can convert negative numbers into positive numbers by taking the absolute of any number or variable.

Practice Questions

1. What is the absolute value of $9$?
2. What is the absolute value of $+5$?
3. What is the absolute value of $|-4|$?
4. Is it true that there are always two numbers with the same absolute value for any given absolute value?
5. What is the absolute value of $3$?
6. What is the absolute value of negative $3$?
7. What is the absolute value of $6$?
8. The absolute value of $-11$ is?
9. What is the absolute value of $5$?
10. What is the absolute value of $12$?
11. What is the absolute value of $-|-8|$?
12. Absolute value of $-11$?
13. What is the absolute value of $-4^{|-4 |}$?

Answer Keys

1. The absolute value of $9$ or $+9$ is always $9$.
2. The absolute value of $+5$ is $5$ or $+5$.
3. The absolute value of $|-4|$ is $4$.
4. This is a tricky question, and the answer to that is no, that is not always the case. You might wonder how it is possible because the absolute value of $-1$ and $1$ is $1$ and, similarly, the absolute value of $-2$ and $2$ is $2$ if we are dealing with whole numbers. We consider the absolute value of “$0$” to be $0$, but “$0$” does not have any negative value, so “$0$” does not have any opposite number whose absolute value is the same.
5. The absolute value of $3$ or $+3$ is $3$.
6. The absolute value of negative $3$ is $3$.
7. The absolute value of $6$ or $+6$ is $6$. 
8. The absolute value of negative $11$ is $11$.
9. The absolute value of $5$ is $5$.
10. The absolute value of $-12$ is $12$.
11. The absolute value of $-|-8|$ is $– 8$.
12. The absolute value of $-11$ is $11$.
13. The absolute value of $-4^{|-4 |}$ is $-4^4 = – 216$.

Conclusion

We can conclude that the absolute value of $-8$ will always be $8$, and we can know it is true because of the following reasons:

• Taking an absolute value of $-8$ is taking the modulus of $-8$, which means that we are only concerned with the magnitude of the number, and the direction or sign of the number is irrelevant hence the absolute value of $-8$ is $8$.
• The absolute value of $-8$ is the distance of “$8$” from the origin. When we take the number “$8$” or “$-8$”, in both cases distance is $8$ because the distance is always positive.