JUMP TO TOPIC

How to find the measure of an angle is an essential skill in various fields, ranging from mathematics and engineering to architecture and navigation.
Whether you’re a student, a professional, or simply an enthusiast eager to delve into the world of angles, this comprehensive guide will equip you with the knowledge and techniques to confidently determine the measure of any angle.
From fundamental concepts to practical methods, we will unravel the mysteries of angle measurement, empowering you to unlock new dimensions in problem-solving, precision, and geometric analysis. Join us on this enlightening journey as we demystify angles, explore measurement tools, and unravel the secrets to accurately determining the measure of an angle.
How to Find Measure of an Angle
To find the measure of an angle, use a protractor placing its midpoint on the angle’s vertex. Read the scale where the angle’s sides intersect the protractor’s edge.
The measure of an angle refers to the degree of rotation between two intersecting lines, rays, or line segments, typically measured in degrees (°).
Determining the measure of an angle is a process of quantifying the amount of rotation or deviation between these geometric elements. It allows us to express the angular relationship between objects, understand their spatial positioning, and solve various mathematical and practical problems.
By employing mathematical principles, measurement tools, and geometric concepts, we can accurately calculate the measure of an angle, enabling us to analyze shapes, construct diagrams, and make informed decisions based on angular information.
Types of Angles
Acute angles
Definition
Acute angles are angles that measure less than 90 degrees.
Explanation
Acute angles are characterized by their sharpness and compactness. They are smaller than a right angle and do not extend beyond it.
Examples
An angle of 30 degrees, 45 degrees, or 60 degrees is considered acute. Examples of real-life acute angles include the corners of a triangle, the hands on a clock at certain times, or the slope of a steep hill.
Obtuse angles
Definition
Obtuse angles are angles that measure between 90 and 180 degrees.
Explanation
Obtuse angles are wider than a right angles. They have a greater degree of openness and appear more spacious than acute angles.
Examples
An angle of 100 degrees, 120 degrees, or 150 degrees is considered obtuse. Examples of real-life obtuse angles include the opening of a wide V-shape, the angle between the hands on a clock at certain times, or the angle formed by a ladder leaning against a wall.
Right angles
Definition
Right angles are angles that measure exactly 90 degrees.
Explanation
Right angles are characterized by their L-shape, forming a perfect quarter turn. They are often associated with perpendicular lines and provide a basis for many geometric constructions and calculations.
Examples
The angle formed by the corner of a square, the intersection of the edges of a cube, or the meeting of two perpendicular lines are all examples of right angles. Right angles are commonly used in architectural drawings, engineering designs, and navigation.
Straight angles
Definition
Straight angles are angles that measure exactly 180 degrees.
Explanation
Straight angles are the largest possible angles, forming a straight line. They are completely flat and lack any curvature or bending.
Examples
A straight angle can be visualized as a line segment or a ray that extends in a straight path without any deviation. It represents a full turn or revolution around a point. Straight angles are commonly encountered in geometry, trigonometry, and circular motion concepts.
Reflex angles
Definition
Reflex angles are angles that measure between 180 and 360 degrees.
Explanation
Reflex angles exceed the measurement of a straight angle and continue beyond it. They extend in a clockwise direction from the initial position of a straight angle.
Examples
An angle of 200 degrees, 270 degrees, or 320 degrees is considered reflex. Examples of real-life reflex angles include the angle formed by the hands on a clock pointing beyond the 6 o’clock mark or the angle between the blades of a rotating windmill.
Full circle
Definition
A full circle is an angle that measures 360 degrees.
Explanation
A full circle represents a complete revolution or a complete trip around a central point. It is comprised of infinite points or angles, all of which sum up to 360 degrees.
Examples
A clock’s dial, a compass, or a circular track are examples of situations where a full circle is encountered. Full circles are fundamental in trigonometry, navigation, and circular geometry, and they are used to calculate bearings, directions, and rotations.
Below we present all the aforementioned angles in figure-1.
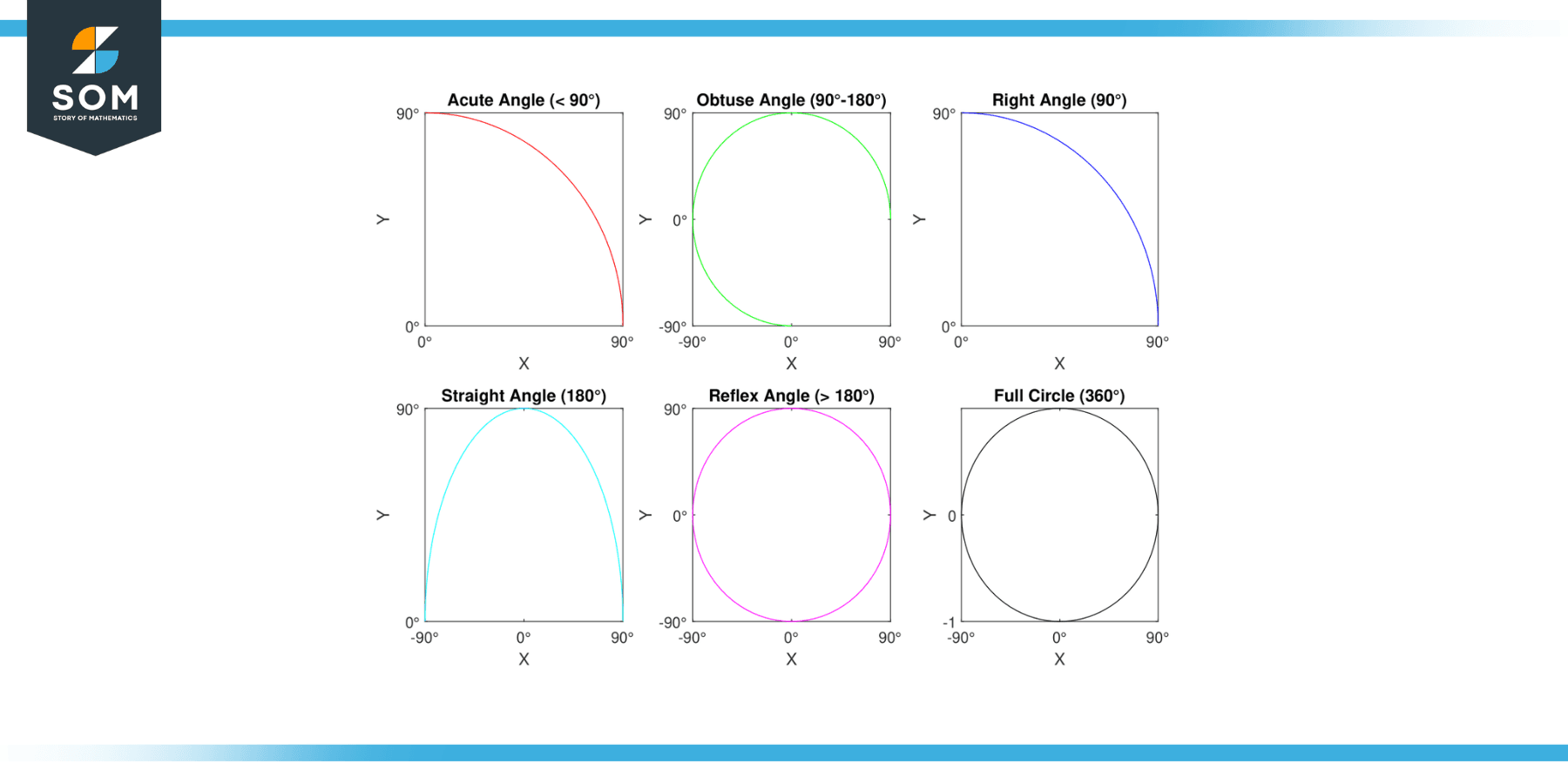
Figure-1.
Common Angle Measurement Techniques
The measure of an angle is typically measured in degrees or radians, and it tells you how much rotation is required to get from one of the angle’s rays (or sides) to the other. Here’s a simple way to measure an angle:
Use a Protractor
A protractor is a semi-circular tool often used in geometry to measure angles. It has degree marks from 0 to 180.
Steps to using a protractor:
- Position the center point of the protractor at the vertex (the point of intersection) of the two sides of the angle.
- Align the zero line of the protractor with one side of the angle.
- Read the value of the protractor where the second side of the angle intersects the protractor. This is the measure of the angle.
Use Trigonometry
If you have a right triangle, you can use the sides of the triangle to compute the measures of the non-right angles.
For example, the tangent of an angle is equal to the length of the side opposite the angle divided by the length of the side adjacent to the angle. So if you know the lengths of these sides, you can use the arctangent function to find the measure of the angle.
Use Geometric Properties
Some angles have measures that can be determined from their geometric properties.
- For example, the angles in a triangle always add up to 180 degrees, so if you know the measures of two of the angles, you can subtract their sum from 180 to find the measure of the third angle.
- As another example, vertical angles (angles across from each other when two lines intersect) are always equal.
Applications
Measurements of angles are used in many fields and contexts. Here are some of them:
Geometry
Geometry is almost entirely about the properties of shapes, many of which involve angles. Angles are used to classify shapes (like triangles and polygons), to find missing sides or angles in triangles, and to prove relationships between shapes.
Trigonometry
The branch of mathematics that deals with the relationships between the sides and angles of triangles is called trigonometry. Trigonometric functions like sine, cosine, and tangent are ratios that relate the angles of a right triangle to the lengths of its sides. These functions have many applications in other fields as well.
Physics
Many aspects of physics, such as the study of forces and motion, use angles. For example, angles are used to calculate the components of vectors, to study pendulum motion, and to analyze the behavior of light and sound waves.
Astronomy
The position of celestial bodies in the sky is defined using angles – typically declination (angle from the celestial equator) and right ascension (angle along the celestial equator).
Additionally, the principle of parallax, which is used to measure the distance of nearby stars, is based on observing the apparent shift of a star from two different points of Earth’s orbit around the sun. The angle of this apparent shift gives a triangle with a known base and allows astronomers to calculate the distance to the star.
Navigation
Traditionally, sailors would use a sextant to measure the angle between the horizon and a celestial body (like the Sun at noon or a star) to find their latitude. Nowadays, in modern GPS technology, the receiver calculates the distance to satellites based on signal travel time.
Knowing these distances and the position of the satellites in space, the receiver can calculate its own position, essentially by triangulation. This is a form of angle measurement in three dimensions.
Architecture and Engineering
In these fields, the principles of geometry and trigonometry are applied to design and construct buildings, bridges, and other structures. For example, the angles between beams or supports can affect the load-bearing capacity of a structure. Also, angles are crucial in designing roof slopes, stair inclines, or any structure or part that is not perpendicular or parallel to others.
Computer Graphics and Game Design
Angles are used in 3D modeling and rendering, where the geometry of a scene is defined in terms of points (or vertices) in three-dimensional space and their connections (forming polygons like triangles). Rotation, scaling, and translation of objects are transformations that involve angle measurements.
In video games, physical simulations like object collisions, reflections, lighting, and shadows all involve computations with angles.
Geography and Cartography
Angles are used in the field of geography to study the Earth’s physical features and climate. In cartography, angles help in making accurate maps and determining distances between locations.
Sports
Many sports involve some understanding of angles, whether implicitly or explicitly. For example, in billiards or pool, players must think about the angles at which to hit the balls to make them go where they want.
Art
Artists use angles to create perspective and depth in their work, especially in drawing and painting.
Exercise
Example 1
In a right triangle, one of the angles is 45 degrees. What is the measure of the other non-right angle?
Solution
In a triangle, the angles add up to 180 degrees. In a right triangle, one of the angles is 90 degrees. So, the other two angles must add up to 90 degrees (because 180 – 90 = 90). If one of these angles is 45 degrees, then the other must also be 45 degrees (because 90 – 45 = 45).
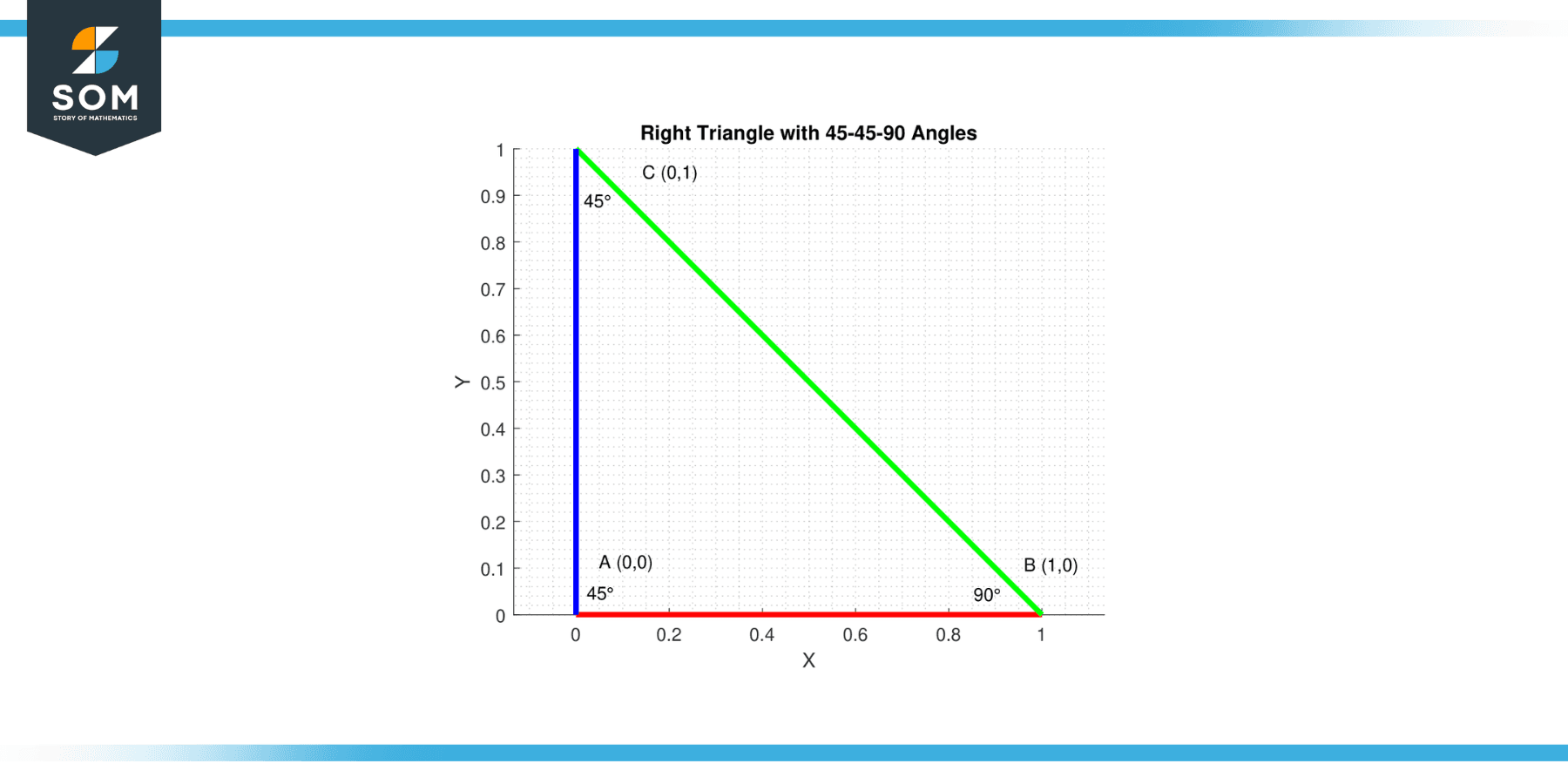
Figure-2.
Example 2
You have an angle that measures 35 degrees. What would be the measure of its supplementary angle?
Solution
Supplementary angles are two angles that add up to 180 degrees. So, to find the measure of an angle that is supplementary to a 35-degree angle, subtract 35 from 180. The result is 145 degrees.
Example 3
You have an angle that measures 80 degrees. What would be the measure of its complementary angle?
Solution
Complementary angles are two angles that add up to 90 degrees. So, to find the measure of an angle that is complementary to an 80-degree angle, subtract 80 from 90. The result is 10 degrees.
Example 4
Two angles are vertical angles, and one measures 120 degrees. What is the measure of the other angle?
Solution
Vertical angles are always equal. Therefore, if one angle measures 120 degrees, the vertical angle to it also measures 120 degrees.
Example 5
In an isosceles triangle, the vertex angle measures 40 degrees. What are the measures of the base angles?
Solution
In an isosceles triangle, the base angles are equal. Furthermore, the sum of the angles in any triangle is 180 degrees. Therefore, the sum of the base angles is 180 – 40 = 140 degrees. Since the base angles are equal, each one measures 140 / 2 = 70 degrees.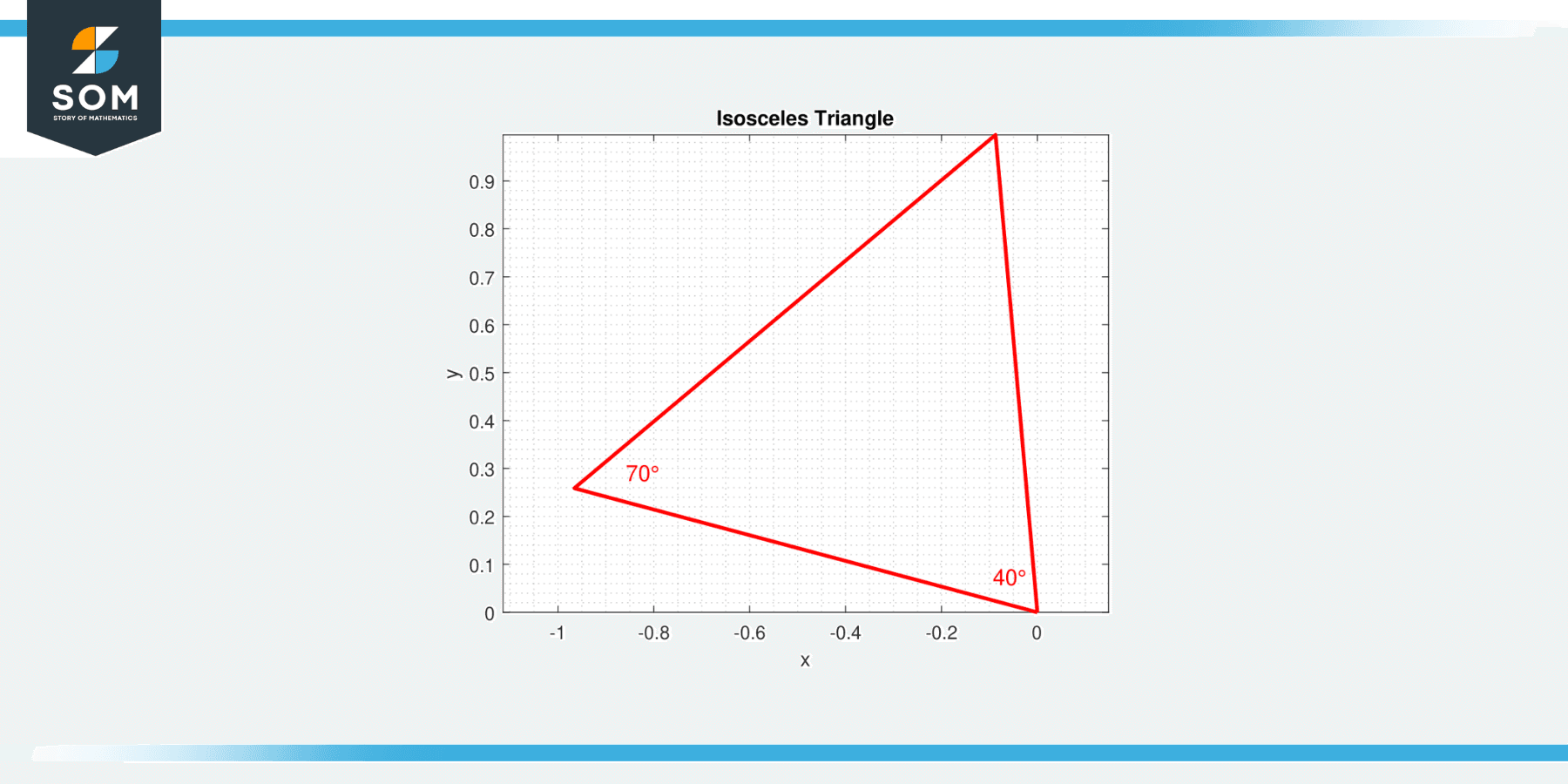
Figure-3.
Example 6
A straight angle is split into two angles. One angle measures 110 degrees. What is the measure of the other angle?
Solution
A straight angle measures 180 degrees. If one angle is 110 degrees, then the other angle is 180 – 110 = 70 degrees.
Example 7
What is the measure of each angle in an equilateral triangle?
Solution
An equilateral triangle has all three sides of equal length, and all three angles are also equal. Since the sum of the angles in any triangle is 180 degrees, each angle in an equilateral triangle measures 180 / 3 = 60 degrees.
Example 8
The measures of the two angles of a triangle are 35 degrees and 65 degrees. What is the measure of the third angle?
Solution: The sum of the angles in a triangle is 180 degrees. If two angles measure 35 and 65 degrees, their sum is 35 + 65 = 100 degrees. Therefore, the third angle measures 180 – 100 = 80 degrees.
All images were created with GeoGebra.
