JUMP TO TOPIC
 Consider a number “$x$”; if it is represented in the form $x^{\dfrac{p}{q}}$, then we will say it is a rational exponent.
Consider a number “$x$”; if it is represented in the form $x^{\dfrac{p}{q}}$, then we will say it is a rational exponent.
Here, “$x$” is the base while $\dfrac{p}{q}$ is the exponent, which we can apply rational exponents’ properties or expressions. Exponents are represented in the radical form and we can apply the properties of rational exponents to solve them.
The basic rules are the same as that of integer exponents, i.e., the numerator is the power of the base, while in contrast, the denominator is the root of the base. This guide will help you understand the concept of rational exponents and how to solve the problems related to them by using their properties.
What Are the Properties of Rational Exponents?
Negative exponents rule, product of the power rule, and product of the quotient rule are just some of the properties of rational exponents. The properties of the rational exponents are pretty similar to the properties of the integer exponents. Simplifying rational exponents is relatively easy as long as you know the properties.
The various properties are given below, along with a detailed explanation of each.
- Negative exponents rule
- Product of the power rule
- Product of the quotient rule
- Power of a product rule
- Power of a quotient rule
- Power of a power rule
- Quotients of power
- Zero exponents
Negative Rational Exponent
If an expression or a number has a negative rational number exponent, then we solve it by taking the inverse of the expression.
$x^{-\dfrac{p}{q}}$ = $\dfrac{1}{x^{\dfrac{p}{q}}}$
Example
$36^{-\frac{1}{2}}$ = $\dfrac{1}{36^{\frac{1}{2}}}$ = $\dfrac{1}{\sqrt{36}}$ = $\dfrac{1}{6}$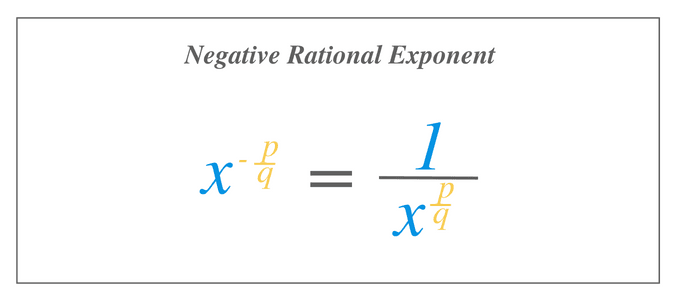
Product of Power
If two same numbers or expression having different/same radical exponents are multiplied with each other, then we add both of the radical exponents.
$x^{\dfrac{p}{q}}. x ^{\dfrac{m}{n}} = x^{\dfrac{p}{q} + \dfrac{m}{n}}$
Example
$27^{\dfrac{8}{3}}. 27^{\dfrac{1}{3}}$ = $27 ^ {\dfrac{1}{9}+ \dfrac{2}{9}}$ = $27^{\dfrac{3}{9}} = 27^{\dfrac{1}{3}}$ = $3$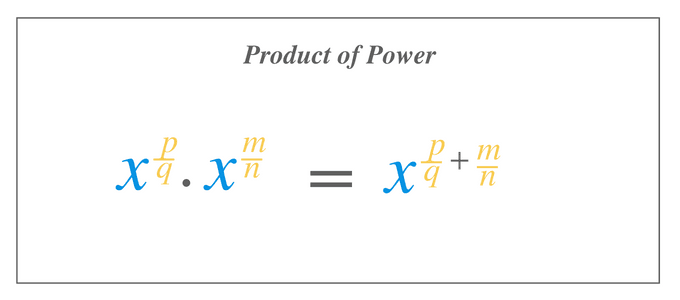
Product of Quotient
If two same numbers or expressions having different/same radical exponents are multiplied with each other, then we add both of the radical exponents.
$\dfrac{x^{\dfrac{p}{q}}}.{x^{\dfrac{m}{n}}}$ = $x^{\dfrac{p}{q} – \dfrac{m}{n}}$
Example
$\dfrac{36^{\dfrac{3}{2}}}.{36^{\dfrac{1}{2}}}$ = $36^{\dfrac{3}{2} – \dfrac{1}{2}}$ = $36^{\dfrac{2}{2}}$ = $36$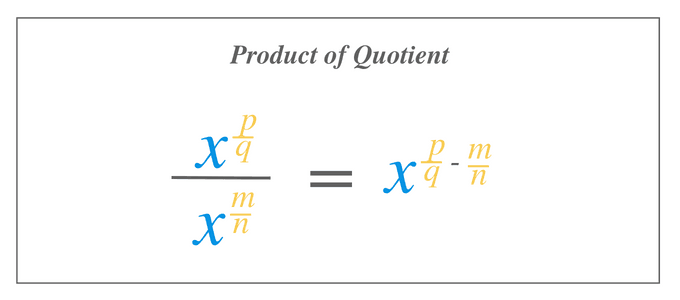
Power of a Product
If two different expressions or a numbers are multiplied with each other while having a rational exponent which is a rational number, then we can write the expression as:
$(x.y)^{\dfrac{p}{q}}$ = $x^{\dfrac{p}{q}}. y^{\dfrac{p}{q}}$
Example
$36^{-\dfrac{1}{2}}$ = $\dfrac{1}{36^{\frac{1}{2}}}$ = $\dfrac{1}{\sqrt{36}} = \dfrac{1}{6}$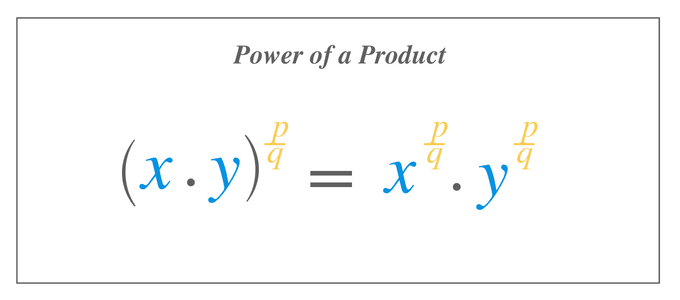
Power of a Quotient
If two different expressions or a numbers are divided with each other while having a common rational exponent, then we can write the expression as:
$(\dfrac{x}{y})^{\dfrac{p}{q}}$ = $\dfrac{x^{\frac{p}{q}}} {y^{\frac{p}{q}}}$
Example
$(\dfrac{16}{9})^{\frac{3}{2}}$ = $\dfrac{16^{\frac{3}{2}}} {9^{\frac{3}{2}}}$ = $\dfrac{4^{3}}{3^{3}}$ = $\dfrac{64}{27}$.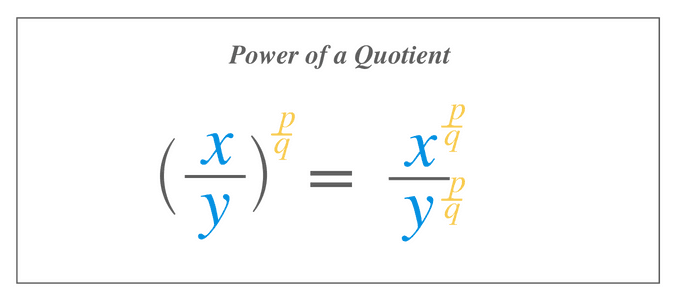
Power of a Power Rule
If an expression or a number with a rational exponent has power as well, then we multiply the power with the rational exponent.
$(x^{\dfrac{p}{q}})^{\dfrac{m}{n}}$ = $x^{(\dfrac{p}{q})(\dfrac{m}{n})}$
Example
$(9^{\frac{3}{2}})^{\dfrac{1}{3}}$ = $9^{(\frac{3}{2})(\frac{1}{3})}$ = $9^{2}$ = $81$
The Power of Power and Power of a Quotient are also known as properties of rational exponents fractions.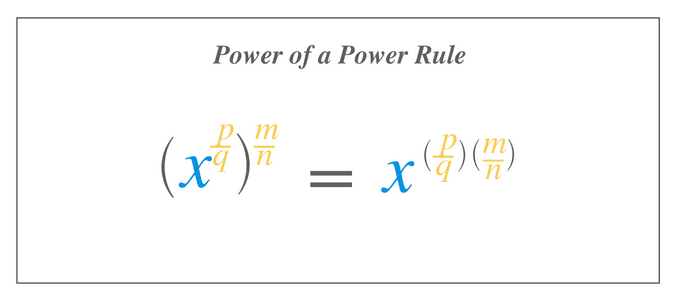
Quotients of Power
If an expression with common bases but different rational number exponents are divided with each other, then we subtract rational exponent of the numerator with the rational exponent of the denominator.
$\dfrac{x^{\frac{p}{q}}}{x^{\frac{m}{n}}}$ = $x^{(\frac{p}{q} – \frac{m}{n})}$
Example
$\dfrac{5^{\frac{3}{2}}}{5^{\frac{1}{2}}}= 5^{(\frac{3}{2} – \frac{1}{2})}= 5^{1} = 5$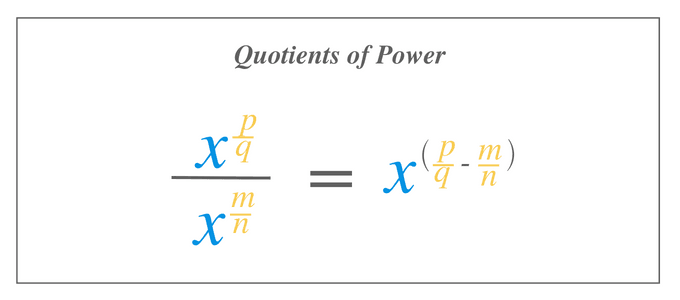
Zero Exponent
If an expression or a number has a zero exponent, then it will be equal to one.
$x^{0} = 1$
Example
$500^{0} = 1$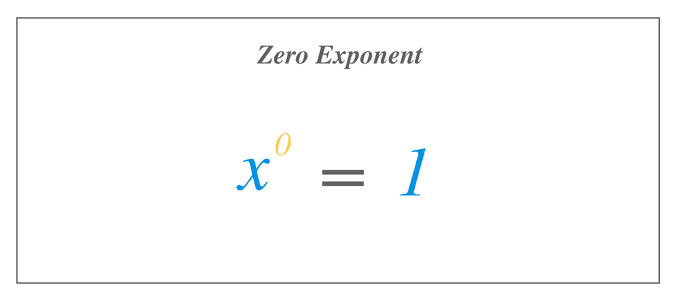
Rational Exponents
An exponent of a number that we can write in rational form is called a rational exponent. For example, the number $x^{m}$ has a rational number exponent, if the “$m$” can be written in $\dfrac{p}{q}$ form: $\large{x}^\tfrac{p}{q}$
We can also write $x^{\dfrac{p}{q}}$ as $\sqrt[q]{x^{p}}$ or $(\sqrt[q]{x})^{p}$.
Different examples of rational number exponents can be written as $3^{\dfrac{4}{3}}$ or $\sqrt[3]{3^{4}}$ or $(\sqrt[3]{3})^{4}$ , $9 ^{\dfrac{11}{5}}$ or $\sqrt[5]{9^{11}}$ or $(\sqrt[5]{9})^{11}$ etc.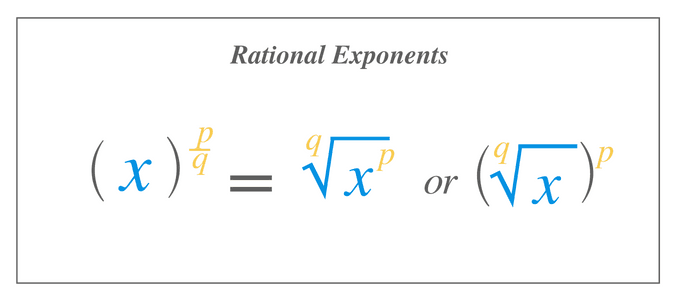
Radicals and Rational Exponents
A Radical and a rational exponent have a direct relation, we can write any rational exponent in the form of radicals, and vice versa. For the rational number exponents to be written as radicals, we need to identify the powers and roots of a given expression and then convert them into radicals.
Consider a rational exponent expression $x^{\dfrac{p}{q}}$, and let us discuss the steps involving the conversion of this rational exponent to a radical expression.
- The first step involves identifying the power of the given expression, and that is the numerator of the rational exponent. For example, $x^{\dfrac{p}{q}}$, $p$ is the power of the expression.
- The second step involves identifying the root of the given expression, and in this case, the root of the expression $x^{\dfrac{p}{q}}$ is “$q$”.
- The final step involves writing the base value as the radicand while the root is written as an index, and the power is written as the power of the radicand. Hence, we can write $x^{\dfrac{p}{q}}$ as $\sqrt[q]{x^{p}}$ or $(\sqrt[q]{x})^{p}$.
Similarly, we can convert radical expressions into rational number exponents. For example, we are given a square root of “$x$” with an index of “$3$” $\sqrt[3]{x}$.We can write this as $x^{\dfrac{1}{3}}$.
We can use the properties of rational exponents and radicals interchangeably to solve complex numerical problems with square roots of exponents.
Rational Exponents Properties in Real-life
Rational exponent properties are used in various mathematical and real-life applications. Some of them are listed below.
- These properties are extensively used in finance numerical questions. Rational exponents are used to determine the financial assets’ interest, depreciation, and appreciation rates.
- These properties are used in solving physics and chemistry complex numerical.
- Radical expressions and usage of their properties are very common in the field of trigonometry and geometry, especially when solving problems related to triangles. Rational exponents are prominently used in construction, masonry, and carpentry.
Example 1:
Solve the following expressions using properties of the rational exponents:
- $8^{\dfrac{1}{3}}.8^{\dfrac{7}{3}}$
- $(4^{\dfrac{1}{2}} . 8^{\dfrac{1}{3}})^{2}$
- $\dfrac{7^{\dfrac{1}{2}}}{7^{1}}$
- $(5^{3}. 4^{3})^{-\frac{1}{3}}$
- $(\dfrac{40^{\frac{1}{5}}}{8^{\frac{1}{5}}})^{2}$
Solution:
1)
$8^{\frac{1}{3}}.8^{\frac{7}{3}} = 8^{(\frac{1}{3}+\frac{7}{3})}$
$= 8^{\frac{8}{3}} = (\sqrt[3]{8})^{8} = (\sqrt[3]{2^{3}})^{8} = 2^{8} = 256$
2)
$(4^{\frac{1}{2}}.8^{\frac{1}{3}})^{2} = (4^{\frac{1}{2}})^{2} . (8^{\frac{1}{3}})^{2} = (\sqrt{4})^{2}. (\sqrt[3]{2^{3}})^{2} = 2^{2}. 2^{2} = 4 . 4 = 16$
3)
$\dfrac{7^{\frac{1}{2}}}{7^{1}} = 7^{(\frac{1}{2} – 1)} = 7 ^{-\frac{1}{2}} = \dfrac{1}{\sqrt{7}}$
4)
$(5^{3}.4^{3})^{-\frac{1}{3}} = ((5.4)^{3})^{-\frac{1}{3}} = (20^{3})^{-\frac{1}{3}} = 20^{-1} = \dfrac{1}{20}$
5)
$\bigg(\dfrac{40^{\frac{1}{5}}}{8^{\frac{1}{5}}}\bigg)^{2} = \bigg[\big(\dfrac{40}{8}\big)^{\dfrac{1}{5}}\bigg]^{2}$ = $(5^ {\frac{1}{5}}) ^{2}$ = $5^{\frac{2}{5}}$
Example 2:
Write the given radicals as a rational exponent:
- $\sqrt[4]{6x}$
- $6\sqrt[3]{5x}$
- $\sqrt[3]{x^{2}}$
- $\sqrt[3]{(5x)^{5}}$
- $7\sqrt[5]{x^{4}}$
Solution:
1)
$\sqrt[4]{6x} = (6x)^{\dfrac{1}{4}}$
2)
$6\sqrt[3]{5x} = 6 (5x)^{\dfrac{1}{3}}$
3)
$\sqrt[3]{x^{2}} = x^{\dfrac{2}{3}}$
4)
$\sqrt[3]{(5x)^{5}}=(5x)^{\dfrac{3}{5}}$
5)
$7\sqrt[5]{x^{4}} = 7 (x)^{\dfrac{4}{5}}$
Example 3:
Write the given rational exponents as radicals:
- $\sqrt[4]{6x}$
- $6\sqrt[3]{5x}$
- $\sqrt[3]{x^{2}}$
- $\sqrt[3]{(5x)^{5}}$
- $7\sqrt[5]{x^{4}}$
Solution:
We have to simplify rational exponents into radical form.
1)
$\sqrt[4]{6x} = (6x)^{\dfrac{1}{4}}$
2)
$6\sqrt[3]{5x} = 6 (5x)^{\dfrac{1}{3}}$
3)
$\sqrt[3]{x^{2}} = x^{\dfrac{2}{3}}$
4)
$\sqrt[3]{(5x)^{5}} = (5x)^{\dfrac{3}{5}}$
5)
$7\sqrt[5]{x^{4}} = 7 (x)^{\dfrac{4}{5}}$
Example 4:
Allan is taking modeling classes to develop different animal models. Let’s assume that the surface area S of the models is given by $S = c m^{\dfrac{1}{3}}$, where “c” is a constant while “m” is the mass of the animals. The constant value of “$c$” is for different animals and it has units $\dfrac{cm^{2}}{grams}$. The value of c for different animals is given below.
| Animal | Mouse | Goat | Horse |
| Value of “c” | $6.5$ | $9.0$ | $14.0$ |
- Determine the surface area of the mouse if the mass of the mouse is $27$ grams.
- Determine the surface area of the goat if the mass of the goat is $64$ Kg.
- Determine the surface area of the horse if the mass of the horse is $216$ Kg.
Solution:
1)
We are given the formula for surface area of the model of animals
$S = cm^{\dfrac{1}{3}}$
The constant value “$c$” for the mouse $= 6.5$
$m = 27$ grams
Plugging both the values in the formula
$S = 6.5 (27^{\dfrac{1}{3}})$
$S = 6.5 (\sqrt[3]{27})^{4}$
$S = 6.5 (3)^{1} = 6.5 \times 3= 19.5 cm^{2}$
2)
We are given the formula for surface area
$S = c m^{\dfrac{4}{3}}$
The constant value “$c$” for the goat = $9.0$
$m = 64$Kg
Plugging both the values in the formula
$S = 9 (64^{\dfrac{4}{3}})$
$S = 9 (\sqrt[3]{64})^{4}$
$S = 9 (4)^{1}$
We have to convert 4 Kg to grams $4Kg = 4000$ grams
$S = 9 (4000) = 36,000 cm^{2}$
3)
We are given the formula for surface area
$S = c m^{\dfrac{4}{3}}$
The constant value “$c$” for the goat $= 14$
$m = 216$ Kg
Plugging both the values in the formula
$S = 14 (216^{\dfrac{1}{3}})$
$S = 9 (\sqrt[3]{216})^{1}$
$S = 9 (6)^{1}$
We have to convert $6$ Kg to grams $6$ Kg = $6000$ grams
$S = 14 (6000) = 84,000 cm^{2}$
Example 5:
Consider you are given two water tankers, “$X$” and “$Y$”. If volume is represented as “$V$” and the formula for the surface area of the tankers is given as $S = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(2V)^{\dfrac{3}{2}}$. If the volume of the tanker “$X$” is $2$ times that of the tanker “$Y$”, then how many times is the surface area of “$X$” bigger than that of “$Y$”?
Solution:
The volume of the tanker “$X$” is two times that of “$Y$”. Hence, the volume of the tanker “$X$” and “$Y$” can be written as:
$V_y = V$
$V_x = 2V$
We are given the surface area formula of the tankers. The surface area formula for tanker “$Y$” will be:
$S_y = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(2V)^{\dfrac{3}{2}}$
If we replace “$V$” with “$2V$” we will get surface area formula for tanker “$X$”.
$S_x = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(2.2V)^{\dfrac{3}{2}}$
$S_x = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(2.V)^{\dfrac{3}{2}}. 2^{\dfrac{3}{2}}$
$S_x = S_y . 2^{\dfrac{3}{2}}$
$\dfrac{S_x}{S_y} = 2.83$ approx.
So the surface area of the tanker “$X$” is $2.83$ times bigger than that of the tanker “$Y$”.
Example 6:
Simplify the following expressions:
- $\dfrac{(3y)^{\dfrac{3}{2}}.(8y)^{\dfrac{5}{2}}.(z)^{\dfrac{7}{2}}}{(y)^{\dfrac{5}{2}}.(z)^{\dfrac{9}{2}}}$
- $4^{3}. (16) ^{\dfrac{3}{2}}. (64)^{\dfrac{1}{3}}$
- $\bigg(\dfrac{x^{\dfrac{1}{2}}.y^{\dfrac{1}{4}}}{x^{-\dfrac{1}{2}}.y^{-\dfrac{1}{4}}}\bigg)$
Solution:
1)
$= (3y)^{\dfrac{3}{2}}.(8)^{\dfrac{5}{2}}.(y)^{\dfrac{5}{2}-\dfrac{5}{2}}.(z)^{\dfrac{7}{2}-\dfrac{9}{2}}$
$= (3y)^{\dfrac{3}{2}}.(8)^{\dfrac{5}{2}}.(y)^{0}.(z)^{-1}$
$= (3y)^{\dfrac{3}{2}}.(2.4)^{\dfrac{5}{2}}.(z)^{-1}$
$= (3y)^{\dfrac{3}{2}}.(2)^{\dfrac{5}{2}}.(4)^{\dfrac{5}{2}}.(z)^{-1}$
$= 32[\dfrac{(3y)^{\dfrac{3}{2}}.(2)^{\dfrac{5}{2}}.(4)^{\dfrac{5}{2}}}{z}]$
2)
$= 4^{3}. (16) ^{\dfrac{3}{2}}. (64)^{\dfrac{1}{3}}$
$= 4^{3}. (4^2) ^{\dfrac{3}{2}}. (4^3)^{\dfrac{1}{3}}$
$= 4^{3}.4^{3}.4$
$= 4^{3+3+1}$
$= 4^{7} =16384$
3)
$= \bigg(\dfrac{x^{\dfrac{1}{2}}.y^{\dfrac{1}{4}}}{x^{-\dfrac{1}{2}}.y^{-\dfrac{1}{4}}}\bigg)$
$= (x^{\dfrac{1}{2}+\dfrac{1}{2}}).(y^{\dfrac{1}{4}+\dfrac{1}{4}})$
$= x.y^{\dfrac{1}{2}}$
Practice Questions
Consider this as a properties of rational exponents worksheet.
1) Consider three water tanks A, B and C. The formula for calculation of volume and surface area of the tanks is given as $V = \dfrac{4}{3}\pi r^{3} cm^{3} and S = \dfrac{4}{3}(\pi)^{\dfrac{2}{3}}(3V)^{\dfrac{3}{2}} cm^{2}$. The radius of all three tanks is given below.
| Tank | A | B | C |
| Radius (cm) | $30$ | $45$ | $40$ |
- Determine the volume and surface area of tank A.
- Determine the volume and surface area of tank B.
- Determine the volume and surface area of tank C.
- Which tank has the largest surface area? You are also required to calculate how much bigger its volume and surface area is compared to other tanks.
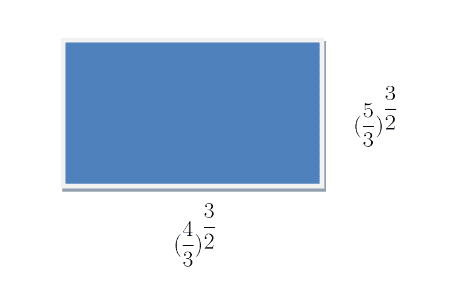
2) Apply properties of rational exponents to determine the area of the rectangle for the figure given below. Side measurements are given in cm.
3) Calculate the area of the square given below.
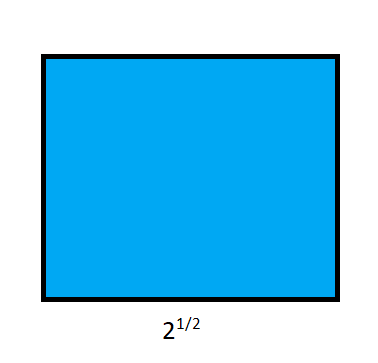
Answer Key
1)
a)
We are given the formula for volume and surface area of the tanks
$V = \dfrac{4}{3}\pi r^{3} cm^{3}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(3V)^{\dfrac{2}{3}} cm^{2}$
The value of the radius for tank $A = 30$ cm. Putting this value in the volume formula we will get
$V = \dfrac{4}{3}\pi (30)^{3} = 113097.6 cm^{3}$
Plugging in the calculated value of volume in the surface area formula.
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(3\times 113097.6)^{\dfrac{2}{3}}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(339292.8)^{\dfrac{2}{3}}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(1621.54)$
$S = 12039 cm^{2}$
b)
We are given the formula for volume and surface area of the tanks
$V = \dfrac{4}{3}\pi r^{3} cm^{3}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(3V)^{\dfrac{2}{3}} cm^{2}$
The value of the radius for tank $A = 45$ cm. Putting this value in the volume formula we will get
$V = \dfrac{4}{3}\pi (45)^{3} = 381704.4 cm^{3}$
Plugging in the calculated value of volume in the surface area formula.
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(3\times 381704.4)^{\dfrac{2}{3}}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(1145113.2)^{\dfrac{2}{3}}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(10945.4)$
$S = 81263.7 cm^{2}$
c)
We are given the formula for volume and surface area of the tanks
$V = \dfrac{4}{3}\pi r^{3} cm^{3}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{1}{3}}(3V)^{\dfrac{2}{3}} cm^{2}$
The value of the radius for tank $A = 40$ cm. Putting this value in the volume formula we will get
$V = \dfrac{4}{3}\pi (40)^{3} = 268083.2 cm^{3}$
Plugging in the calculated value of volume in the surface area formula.
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(3\times 268083.2)^{\dfrac{2}{3}}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(804249.6)^{\dfrac{2}{3}}$
$S = \dfrac{4}{3}(\pi)^{\dfrac{3}{2}}(8648.2)$
$S = 64208.2 cm^{2}$
d)
Tank B has the largest volume and surface area among all the tanks. We can calculate how much bigger its volume and surface area is compared to other tanks by taking the ratio.
$\dfrac{Volume\hspace{2mm}of\hspace{2mm}tank\hspace{2mm} B}{Volume\hspace{2mm} of\hspace{2mm} tank\hspace{2mm} A} = \dfrac{381704.4}{113097.6} = 3.375$
The volume of tank B is $3.375$ times bigger than that of tank A.
$\dfrac{Surface\hspace{2mm} Area\hspace{2mm} of\hspace{2mm} tank\hspace{2mm} B}{Surface \hspace{2mm}Area\hspace{2mm} of\hspace{2mm} tank\hspace{2mm} A} = \dfrac{81263.7}{12039} = 6.75$
The surface area of tank B is $6.75 times bigger than that of tank A.
$\dfrac{Volume\hspace{2mm} of \hspace{2mm}tank \hspace{2mm}B}{Volume\hspace{2mm} of\hspace{2mm} tank\hspace{2mm} C} = \dfrac{381704.4}{268083.2} = 1.42$
The volume of tank B is $1.42$ times bigger than that of tank C.
$\dfrac{Surface\hspace{2mm} Area\hspace{2mm} of\hspace{2mm} tank \hspace{2mm}B}{Surface\hspace{2mm} Area\hspace{2mm} of \hspace{2mm}tank \hspace{2mm}C} = \dfrac{81263.7}{64208.2} = 1.27$
The surface area of tank B is $1.27$ times bigger than that of tank C.
2)
Formula for the area of the rectangle is:
$Area = Length \times Width$
$Area = (\dfrac{4}{3})^{\dfrac{3}{2}} \times (\dfrac{5}{3})^{\dfrac{3}{2}}$
$Area = (\dfrac{4}{3}. \dfrac{5}{3})^{\dfrac{3}{2}}$
$Area = (\dfrac{20}{9})^{\dfrac{3}{2}} = 3.13 cm^{2}$
3)
The formula for the area of the square is:
Area $= Side \times Side$
We are given the value of one side as $2^{\dfrac{1}{2}}$
Area of the square $= 2^{\dfrac{1}{2}} \times 2^{\dfrac{1}{2}}$
Area of the square $= 2 \times 2 = 4$
