Equilateral Triangles – Essential Concepts with Examples

The equilateral triangle is a fascinating and significant geometric shape with a particular place in the geometry study. This specific triangle has three sides that are of the same length. The equilateral triangle differs from other kinds of triangles, which can have sides of varied lengths because of this special quality.

This article will thoroughly explore the unique attributes, characteristics, and mathematical formulas intrinsic to the equilateral triangle. Our investigation will encompass an in-depth analysis of its structural elements, angle measurements, and the interplay between its sides. Furthermore, we shall delve into precise methodologies for computing the equilateral triangle’s area and perimeter. Additionally, we will shed light on this geometric shape’s practical significance and applications across various domains.

Definition of the Equilateral Triangle

The term “Equilateral” is derived from the combination of “Equi” and “Lateral,” both of which imply the notion of sides. Due to the same length of its sides an equilateral triangle is also referred to as a regular polygon or regular triangle, owing to the equal length of its sides. It is classified as an equilateral triangle when all three sides and angles are congruent—specifically, each angle within an equilateral triangle measures precisely 60 degrees. 

Its angles are congruent, meaning they have the exact measurements, and all sides have identical lengths. Each angle in an equilateral triangle is precisely 60 degrees in length. Furthermore, the angle sum property of triangles holds, as the collective sum of these angles amounts to 180 degrees. The equilateral triangle has a sense of harmony, symmetry, and aesthetic appeal thanks to the equality of side lengths and angle measures.

The equilateral triangle is significant in many areas, including mathematics, architecture, engineering, and design, because of its unique properties and appealing features.
It is regularly incorporated into structures and patterns to elicit a sense of harmony and visual attractiveness because of its symmetrical and proportionate nature in art and architecture.

Shape Description

An equilateral triangle is a straightforward yet beautiful geometric geometry that has three equal sides and three equal angles. It resembles a regular triangle with all sides having the same length. When the triangle’s three corners meet, they form three straight lines. The equilateral triangle exhibits a balanced and symmetrical appearance, making it visually pleasing.

In terms of dimensions, an equilateral triangle possesses the following properties.

Sides

An equilateral triangle is characterized by having three sides of equal length. Consequently, the line segments connecting the triangle’s three vertices are all the same length.

Angles

In an equilateral triangle, all three angles are congruent, meaning they have the same measure. Specifically, each angle within an equilateral triangle measures precisely 60 degrees. This uniform angle measure enhances the symmetry of the triangular shape, contributing to its visually pleasing appearance.

Vertex

The three corners or spots where the triangle’s sides intersect are known as the vertices of an equilateral triangle. In an equilateral triangle, all three vertices are sharp and contribute to the triangular shape of the figure.

Lines and Segments 

The sides of an equilateral triangle consist of straight lines that connect its vertices. These lines share the property of being congruent in length and collectively form the three edges of the triangle. Furthermore, the various segments within an equilateral triangle, such as the altitude (a perpendicular segment from a vertex to the opposite side) and the median (a segment connecting a vertex to the midpoint of the opposite side), exhibit specific relationships that arise from the triangle’s inherent symmetry.

Symmetry

An equilateral triangle exhibits remarkable symmetry through multiple lines. The three medians of an equilateral triangle, which are segments connecting each vertex to the midpoint of the opposite side, intersect at a point known as the centroid. This centroid serves as the center of symmetry for the triangle.

Additionally, the equilateral triangle possesses rotational symmetry of order 3. This means it can be rotated by multiples of 120 degrees around its centroid and maintain its identical appearance. This rotational symmetry further highlights the balanced and harmonious nature of the equilateral triangle.

Regularity

The equilateral triangle belongs to the category of regular polygons. A regular polygon is characterized by having all sides and angles congruent. Specifically, in the case of the equilateral triangle, all three sides and angles are equal in measure, satisfying the conditions of a regular polygon.

Below is the geometrical diagram for an equilateral triangle.

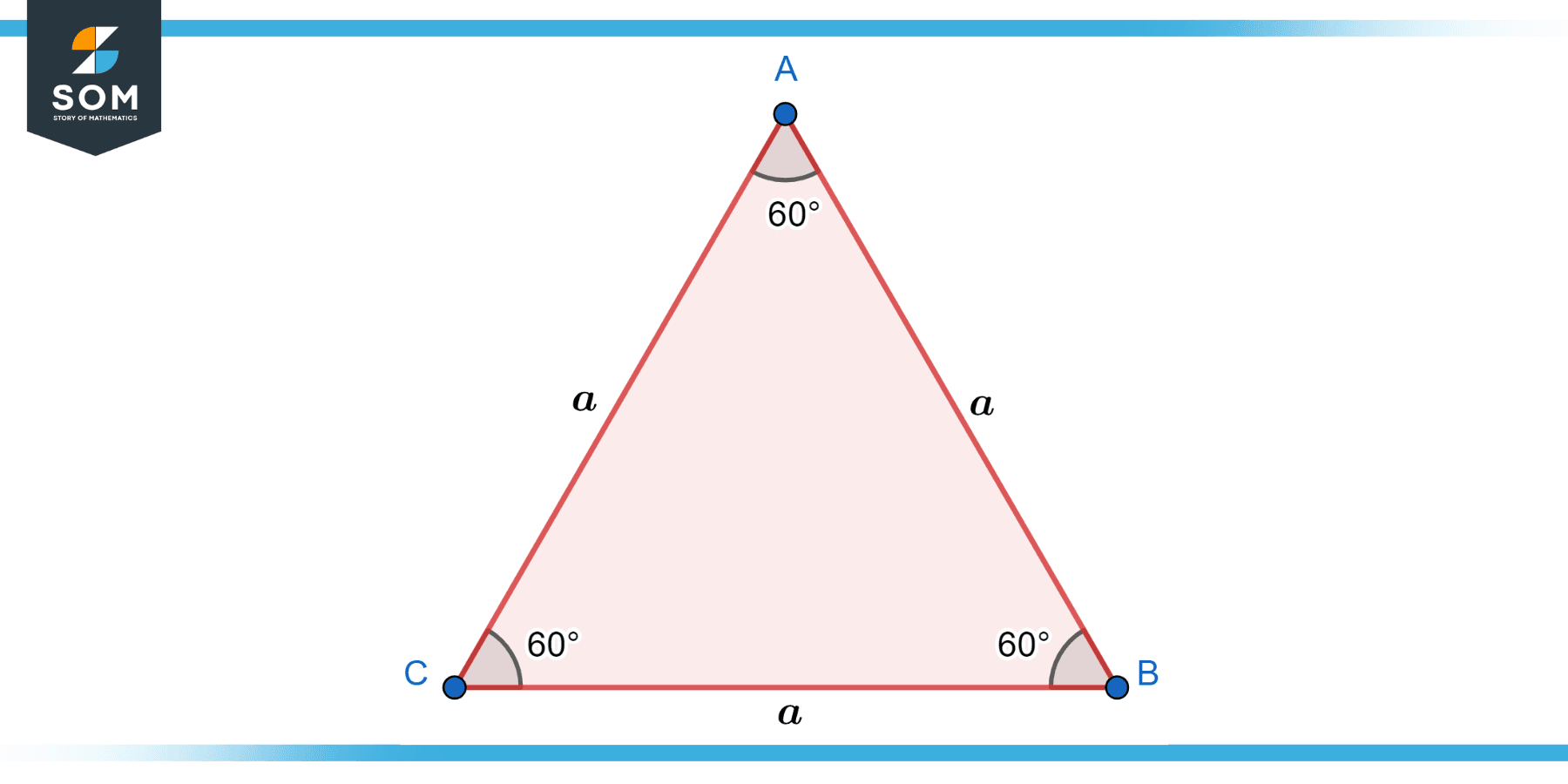
Figure 1

Attributes

An equilateral triangle possesses specific attributes that distinguish it as a unique type. To identify an equilateral triangle, consider the following properties as indicators.

• The sides of an equilateral triangle have equal measurements.
• The angles of an equilateral triangle are congruent, and each measures 60 degrees.
• Triangle ABC is an equilateral triangle because its sides, AB, BC, and AC, are all of equal length, or AB = BC = AC, i.e., ∠A = ∠B = ∠C = 60°
• The equilateral triangle is a regular polygon due to its three sides.
• In an equilateral triangle, if a perpendicular is drawn from any vertex to the opposite side, it will bisect the side into two equal lengths. Additionally, the perpendicular will divide the angle at the vertex into two halves, each measuring 30 degrees.
• The orthocenter and centroid of an equilateral triangle coincide at the same point.
• In an equilateral triangle, the medians, angle bisectors, and altitudes originating from each vertex are identical for all three sides.
• The sum of all the angles in an equilateral triangle equals 180 degrees.

And many more.

Relevant Formulae

Side Length and Perimeter

The perimeter of an equilateral triangle can indeed be calculated by multiplying the length of any one side, denoted by “s,” by three. So, the formula for the perimeter, denoted by “P,” is P = 3s. This means the perimeter is three times the length of any one side of the equilateral triangle.

Interior Angles

In an equilateral triangle, each interior angle measures 60 degrees. This is so that the triangle’s three angles, which are all congruent and each measure 60 degrees, must total up to 180 degrees. The equilateral triangle exhibits this consistent angle measurement, contributing to its symmetrical and balanced appearance.

Altitude and Height

In an equilateral triangle, the altitude is a line segment drawn from one vertex perpendicular to the opposite side. This altitude also serves as the height of the triangle. The height, denoted by “h,” can be calculated using the formula:

$$h = \frac{\sqrt{3}}{2} \times s$$

Where s represents the length of the side of the equilateral triangle, by substituting the side length into the formula, one can determine the height of the equilateral triangle.

Area

The area of an equilateral triangle can be calculated using the formula:

$$A = \frac{s^2 \sqrt{3}}{4}$$

Where s represents the length of the side of the equilateral triangle. By substituting the side length into the formula, you can determine the area of the equilateral triangle.  Thus, the area formula involves multiplying the side length squared by the square root of 3 and dividing the result by 4.

Centroid

The centroid of an equilateral triangle lies at the center of the triangle. Since all sides of the equilateral triangle are equal in length, finding the centroid is a straightforward process. To locate the centroid, perpendicular lines are drawn from each triangle vertex to the opposite side. These perpendicular lines, known as medians, are all equal in length and intersect at a single point, precisely the equilateral triangle’s centroid. The centroid divides each median into two segments, with the segment connecting the vertex to the centroid being twice as long as the segment connecting the centroid to the midpoint of the opposite side. Below in Figure-2, the centroid for an equilateral triangle is depicted.

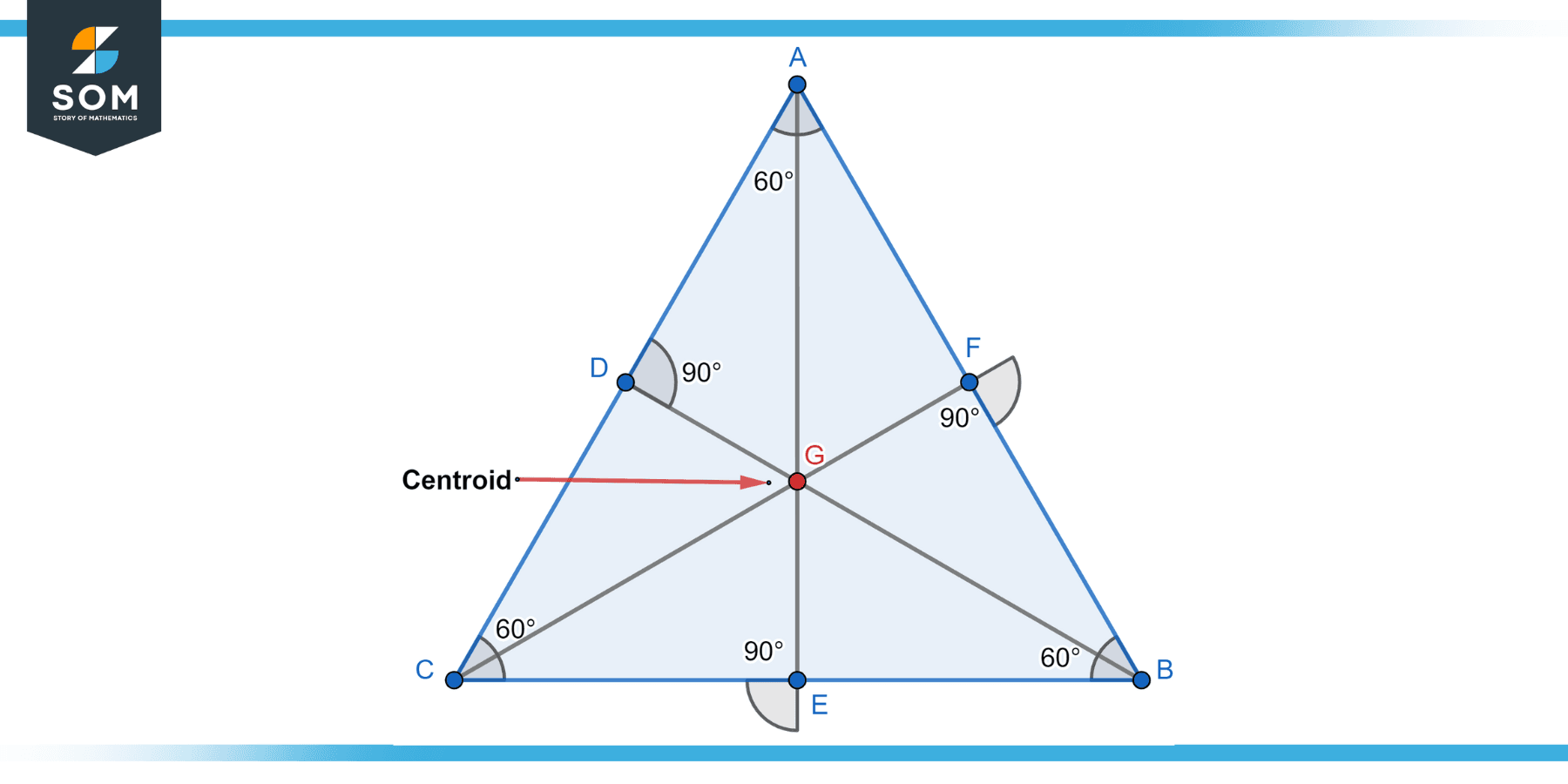
Figure-2: Equiletral triangle centroid.

Applications of Equilateral Triangle

Equilateral triangles find practical applications in various fields due to their unique properties and balanced structure. Here are a few notable applications.

Architecture and Engineering

Equilateral triangles play a crucial role in architecture and engineering, providing essential support for the structural integrity of buildings, bridges, and various structures. Their inherent equilibrium and balance allow them to withstand external forces, ensuring stability and durability effectively.

Computer Graphics and Design

Equilateral triangles serve as fundamental elements in the creation of three-dimensional objects and the generation of geometric patterns in the realm of computer graphics. Intricate and visually captivating designs can be meticulously crafted using these triangles, adding depth and complexity to digital imagery.

Trigonometry and Mathematics

Within trigonometry, equilateral triangles serve as foundational elements that enable the derivation of trigonometric functions and identities. These triangles play a crucial role in the study of ratios, angles, and the relationships between the sides of a triangle. By examining the properties and measurements of equilateral triangles, students and mathematicians can develop a deeper understanding of fundamental trigonometric concepts and expand their knowledge in this field of mathematics.

Robotics

Equilateral triangles find applications in robotics, especially in the design of robotic arms and mechanisms. The stability provided by equilateral triangles assists in precise movements, control, and efficient load distribution in robotic systems.

Surveying and Navigation

Equilateral triangles have practical applications in surveying and navigation. Land surveyors use the geometry of equilateral triangles to accurately measure angles and distances on the field. Similarly, navigational tools like compasses and astrolabes utilize equilateral triangles to determine direction and calculate bearings.

Traffic Signaling

Equilateral triangles are widely used in traffic signaling systems. Triangular road signs, such as yield signs and warning signs, often feature an equilateral shape. The distinctiveness of equilateral triangles helps drivers recognize important instructions and take appropriate actions on the road.

Crystallography

Equilateral triangles play a crucial role in crystallography, the study of crystal structures. The arrangement of atoms or molecules in certain crystal lattice structures can form equilateral triangles, aiding scientists in understanding the properties and behavior of crystals.

Chemistry

Equilateral triangles play a significant role in chemistry, particularly in examining crystal structures and determining atom arrangements within a lattice. By studying the symmetrical nature of equilateral triangles within the crystal lattice, scientists can gain insights into the properties and behavior of materials at the atomic level. Understanding the structure and composition of crystals, which in turn affects their physical and chemical properties, is crucial for improving our understanding of chemistry and related sciences. By utilizing equilateral triangles as a tool in crystallography, researchers can make significant contributions to various fields, including materials science, solid-state physics, and chemistry.

Exercise

Example 1

Find the area of the equilateral triangle given in Figure-3.

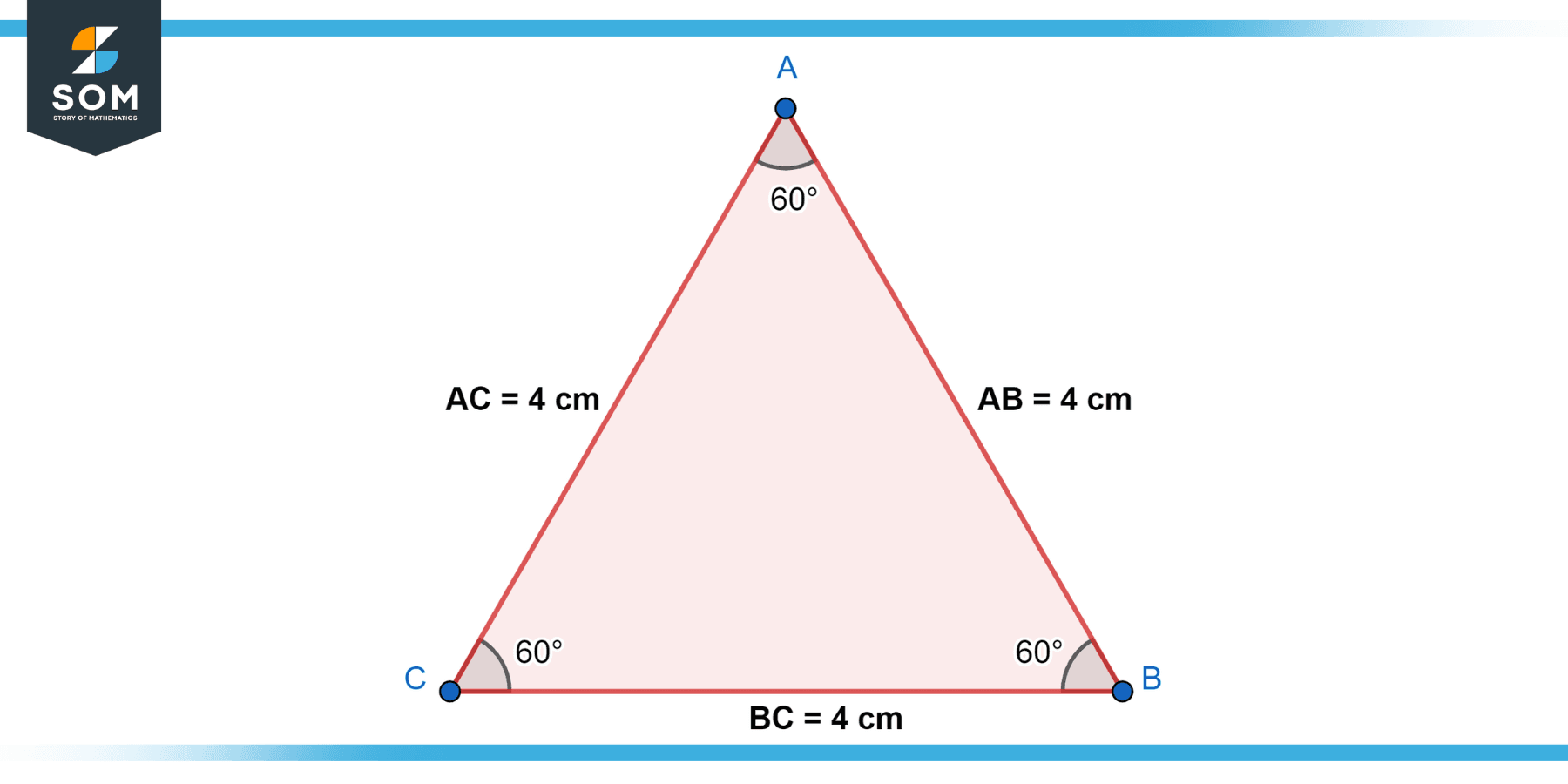
Figure-3

Solution

To find the area of an equilateral triangle, we can use the formula:

$$ A = \frac{s^2\sqrt{3}}{4} $$

Where A represents the area, and s represents the side length of the equilateral triangle.

In this case, the side length (s) of the equilateral triangle ABC is 4 cm.

Substituting the value of s into the formula, we get:

$$ A = \frac{4^2\sqrt{3}}{4} $$

Simplifying the expression, we have:

$$ A = \frac{16\sqrt{3}}{4} $$

$$ A = 4\sqrt{3}$$

Therefore, the area of an equilateral triangle ABC is $\boldsymbol{{4\sqrt{3}}}$ square centimeters.

Example 2

What is the perimeter of an equilateral triangle with a side length of s = 8 units?

Solution

The perimeter of an equilateral triangle can be calculated by multiplying the length of any one side by three. In this case, the side length is s = 8 units.

P = 3 × s

P = 3 × 8

P = 24 units

Therefore, the perimeter of an equilateral triangle with a side length of 8 units is 24 units.

Example 3

What is the length (s) of each side of an equilateral triangle if its perimeter is 30 meters?

Solution

To find the length of each side of an equilateral triangle when the perimeter is known, we divide the perimeter by 3 since all sides are equal.

P = 30 meters

s = P/3

s = 30/3

s = 10 meters

Therefore, each side of the equilateral triangle is 10 meters long.

Example 4

Calculate the height (h) of an equilateral triangle with a side length of 16 inches.

Solution

To calculate the height of an equilateral triangle, we can use the formula:

$$h = \frac{\sqrt{3}}{2} \times s$$

Given that the side length is 16 inches, we can substitute this value into the formula:

$$h = \frac{\sqrt{3}}{2} \times 16 \ \textrm{inches}$$

$$h = \frac{1.732}{2} \times 16 \ \textrm{inches}$$

h = 0.0866 × 16 inches

h = 13.856 inches

Therefore, the height of the equilateral triangle with a side length of 16 inches is approximately 13.856 inches.

Example 5

If the area of an equilateral triangle is 36 square units, what is the length (s) of each side?

Solution

To find the length of each side of an equilateral triangle given its area, we can use the following formula:

$$s = \sqrt{\frac{4 \times A}{\sqrt{3}}}$$

Given that the area is 36 square units, we can substitute this value into the formula:

$$s = \sqrt{\frac{4 \times 36}{\sqrt{3}}}$$

$$s = \sqrt{\frac{144}{\sqrt{3}}}$$

$$s = \frac{\sqrt{144}}{\sqrt{\sqrt{3}}}$$

$$s = \frac{12}{\sqrt{\sqrt{3}}}$$

Simplifying the expression $\sqrt{\sqrt{3}}$, we get:

s = 121.732

s = 6.928

Therefore, the length of each side of the equilateral triangle with an area of 36 square units is approximately 6.928 units.

Example 6

For the equilateral triangle given in Figure-4, calculate the length (s) of each side of the triangle.

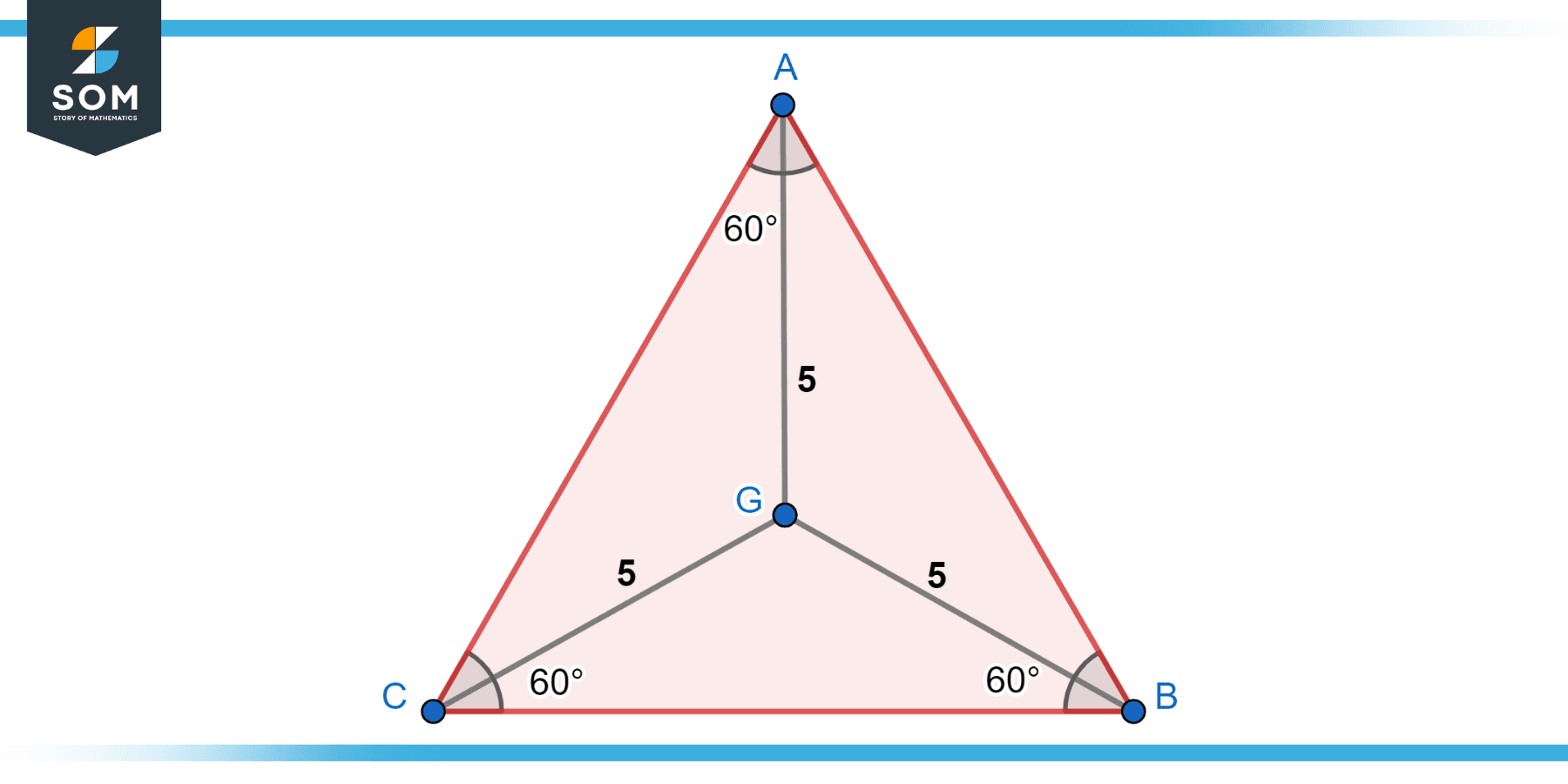
Figure-4

Solution

In an equilateral triangle, the centroid divides each median (segment connecting a vertex to the midpoint of the opposite side) in a 2:1 ratio. The length of each side of the triangle can be calculated as follows, given that the distance between each vertex and the centroid is 5 units:

Let’s use x to symbolize each side’s length.

From the centroid to each vertex, we have two segments: one segment of length 2x/3 and another segment of length x/3 (since the ratio of lengths is 2:1).

According to the given information, the length of each segment is 5 units. Therefore, we can set up the following equation:

2x/3 = 5

To solve for x, we can multiply both sides of the equation by 3/2:

2x/3 × 3/2 = 5 × 3/2

x = 7.5

Hence, each side of the equilateral triangle is 7.5 units.

Example 7

How many sides are there in total when an equilateral triangle is divided into smaller congruent equilateral triangles by connecting the midpoints of its sides, given that there are 16 small equilateral triangles?

Solution

Let’s start by considering the original equilateral triangle. It has three sides.

When we connect the midpoints of its sides, we create four smaller equilateral triangles within it. Each of these smaller triangles also has three sides.

If we continue this process, we can see that the number of smaller triangles doubles with each iteration: 1, 4, 8, 16.

Since there are 16 small equilateral triangles, we can calculate the total number of sides in all the triangles combined as follows:

Number of sides = Number of triangles × Number of sides per triangle 

Number of sides = 16 × 3

Number of sides = 48

Therefore, there are a total of 48 sides in all the triangles combined.