JUMP TO TOPIC
 In mathematics, more importantly in multivariable calculus, the implicit function theorem is used to solve polynomial equations that cannot be expressed as a function.
In mathematics, more importantly in multivariable calculus, the implicit function theorem is used to solve polynomial equations that cannot be expressed as a function.
We state it for a two-variable relation as follows:
Let $f(x,y)$ is a relation with $f(x_0, y_0) = c$ and $f’_y(x_0, y_0) \neq 0$; then around $(x_0, y_0)$ there exists a unique differentiable function $y(x)$ that satisfies $f(x, y(x))=c$ and $y'(x) = \frac{\partial_yf(x,y)}{\partial_xf(x,y)}$
In this topic, we will study the implicit function theorem, its proof and the applications of implicit function theorem.
What Is Implicit Function Theorem?
An implicit function theorem is a theorem that is used for the differentiation of functions that cannot be represented in the $y = f(x)$ form. For example, consider a circle having a radius of $1$.
The equation can be written as $x^{2}\hspace{1mm}+ \hspace{1mm}y^{2}=1$. There is no way to represent a unit circle as a graph of $y = f(x)$. So, $x^{2}+ y^{2}=1$ is not a function because for each value of “$x$”, there are two values of “$y$”, a positive and a negative, as can be seen in the picture below.
Remember that a relation between $x$ and $y$ is called a function if, for each value of $x$, there is only one value of $y$.
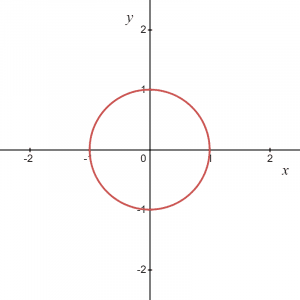
So we know that the equation of a circle is not a function, but it is still a relationship between two variables “$x$” and “$y$” and the equation for variable “$y$” can be written as $\pm\sqrt{1\hspace{1mm}-\hspace{1mm}x^{2}}$.
So, as the equation suggests, for each value of “x”, we have two values of “y”. If we take the circle graph as a whole, it is not a function, but if we consider some local point or just a positive or negative arc of a circle graph, it gives us a function.
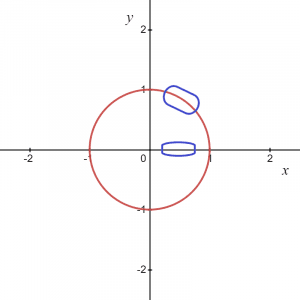
For the picture given above, we know that the marked area can be given as $y = \sqrt{1\hspace{1mm}-\hspace{1mm}x^{2}}$, so this gives us a function and similarly, if we take an arc in the negative coordinate then the function can be written as $y = -\sqrt {1- x^{2}}$.
However, on two points, i.e., $(-1,0)$ and $(1,0)$, we will have two values of “$y$” for one value of “$x$”, so we can conclude that the two assumed functions $y_1 = \sqrt{1\hspace{1mm}-\hspace{1mm}x^{2}}$ and $y_2 = -\sqrt {1\hspace{1mm}-\hspace{1mm} x^{2}}$ are explicit functions and will give the same relation as that of original equation $x^{2}\hspace{1mm}+\hspace{1mm} y^{2}=1$ for any local points apart from two points on x-axis $(1,0)$ and $(-1,0)$.
We segregated the original equation into two explicit functions in the above example. The implicit function theorem does the same for any given implicit equation given in the form $F(x,y) = 0$. It can be written in the form $y = f(x)$ at some local points, provided that certain conditions for implicit function theorem are met.
Implicit function theorem will not give us the formulas for respective explicit functions of $F (x,y)$. Instead, it will tell us whether or not any explicit function for $F(x,y)$ exists and how to find the derivative — this is why it is called implicit function theorem.
Implicit Function
Implicit function theorem converts different complex non-linear relations to sub-functions that can further be differentiated to solve the problem. To fully understand the concept of the implicit function theorem, it is also necessary to understand the definition of an implicit function.
Implicit function is a function that is represented in the form of implicit equation. It cannot be represented in the form $y = f(x)$. For example, the equation $x^{2}\hspace{1mm} – \hspace{1mm}y^{2} = 1$ is an implicit equation while the equation $y = 4x\hspace{1mm} +\hspace{1mm}6$ represents an explicit function.
How To Use Implicit Function Theorem
The implicit function theorem theoretical explanation may look tedious, but it is quite easy to use in numerical examples. Keep in mind the properties of implicit function theorem listed below while solving numerical examples.
- We use partial differentiation while solving examples using the implicit function theorem.
- While solving for one variable, the rest of the variables are considered constant.
- Once the respective variables’ differentiation has been carried out, the calculated values are put in the implicit function theorem formula to get the final answer.
Implicit Function Theorem Proof
We will prove that $F(x,y)$ can be written as a function $y = f(x)$ in the neighborhood of coordinates $(x_o,y_o)$. This proof then will help us in developing the formula for implicit function theorem derivative and it that can be given as:
$f'(x) = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}$
We will develop the formula for two-variable cases only. To prove this theorem, we have to make some assumptions.
Assume $F(x,y)$ is continuous near $(x_o, y_o)$. Let us say $F(x,y)$ is continuous at point “$c$” near $(x_o, y_o)$ such that we have following conditions:
1) $F(x_o,y_o) = 0$
2) $\dfrac{\partial F}{\partial y} \neq 0$
3) $\dfrac{\partial F}{\partial y} > 0$ this can be negative depending upon function, but for the sake of our proof, let us take this as positive.
As $F(x,y)$ is continuous near the $(x_0, y_o)$, hence the partial derivative of function “F” will be continuous as well. Hence $\dfrac{\partial F}{\partial y} > 0$ and is continuous.
Now, if we fix the value of “$x$” at “$x_o$” and vary the value of “$y$”, we get the function $F(x_o, y)$. If we differentiate this function w.r.t to “$y$”, the function will be an increasing function.
But just as we discussed in the circle example earlier, if we fix the value of one variable and vary the other, then at some point, it will have a negative value so that we can write:
$F(x_0, y_1) > 0$
$F(x_o, y_2) < 0$
So the function is positive at some point “$y_1$” and negative at some point “$y_2$”. Remember both these points are in the neighborhood of point “c” and as the function $F(x_o,y_o)$ was continuous, so will these two functions also be continuous increasing functions.
So if we take any point “$x$” near “$x_o$”, then $F(x,y_1) > 0$ and $F(x,y_2) < 0$ and we know both these functions will be continuous as the point “$x$” is in the neighborhood of point “$x_o$”. Now, if we continue to vary the value of the variable “$y$” and find a unique value of “$y$” between “$y_1$” and “$y_2$”, that makes the function equal to zero, then we can write:
For a unique value of “$y$” $F (x,y) = 0$
Hence it is proved that $F(x,y) = 0$, it is continuous and has a unique solution so we can say that $y =f(x)$.
Now let us prove the derivative formula for the implicit function theorem.
$F(x,y) = 0$
We know $y = f(x)$.
Let us plug in the value and we get:
$F(x, f(x)) = 0$
Now taking derivative on both sides
$(\dfrac{\partial F}{\partial x}.\dfrac{\partial}{\partial x}x) + (\dfrac{\partial F}{\partial y})f'(x)$
So, now we can solve for $f'(x)$.
$f'(x) = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}$
Hence it is proven. This proof had all the necessary theoretical explanation included in it for better understanding.
Let us discuss implicit function theorem examples.
Example 1
Consider the equation for a circle having a radius “$1$”. Use implicit function theorem to find the formula for the slope of the tangent at any given point $(x,y)$ on the circle.
Solution:
We know that the equation for a circle having radius 1 can be written as:
$x^{2}\hspace{1mm}+\hspace{1mm} y^{2}= 1$
$x^{2}\hspace{1mm}+\hspace{1mm} y^{2} -1 = 0$ (1)
The formula for implicit function theorem is given as:
$f'(x) = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}$
While taking the partial derivative of variable “x” ,the variable “y” will be considered as constant; and similarly, while taking the partial derivative of variable “y”, the variable “x” will be taken as constant.
$\dfrac{\partial F}{\partial x} = \dfrac{\partial}{\partial x}( x^{2}\hspace{1mm}+\hspace{1mm} y^{2}\hspace{1mm} -\hspace{1mm}1)$
$\dfrac{\partial F}{\partial x} = 2x \hspace{1mm}+\hspace{1mm} 0 \hspace{1mm}– \hspace{1mm}0$
$\dfrac{\partial F}{\partial x} = 2x
$\dfrac{\partial F}{\partial y} = \dfrac{\partial}{\partial y}( x^{2}\hspace{1mm}+ \hspace{1mm}y^{2}\hspace{1mm} -\hspace{1mm}1)$
$\dfrac{\partial F}{\partial y} = 0\hspace{1mm} +\hspace{1mm} 2y\hspace{1mm} –\hspace{1mm} 0$
$\dfrac{\partial F}{\partial y} = 2y$
Now put both the partial derivative values in the implicit function theorem formula:
$f'(x) = – \dfrac{2x}{2y}$
Example 2
Find the derivative of the polynomial equation $2x^{2}\hspace{1mm}-\hspace{1mm}4y^{2} = 6 $using implicit function theorem.
Solution:
First, we have to write the equation in the form $F(x,y) = 0$
$2x^{2}\hspace{1mm}- \hspace{1mm}4y^{2} = 6$
$2x^{2}\hspace{1mm}- \hspace{1mm}4y^{2}\hspace{1mm} -\hspace{1mm} 6 = 0$
The formula for implicit function theorem is given as:
$f'(x) = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}$
$\dfrac{\partial F}{\partial x} = \dfrac{\partial}{\partial x}(2 x^{2}\hspace{1mm}-\hspace{1mm} 4y^{2}\hspace{1mm} –\hspace{1mm} 6)$
$\dfrac{\partial F}{\partial x} = 2\times 2x\hspace{1mm} – \hspace{1mm}0 \hspace{1mm}– \hspace{1mm}0$
$\dfrac{\partial F}{\partial x} = 4x$
$\dfrac{\partial F}{\partial y} = \dfrac{\partial}{\partial y}(2 x^{2}\hspace{1mm}-\hspace{1mm} 4y^{2}\hspace{1mm} –\hspace{1mm} 6)$
$\dfrac{\partial F}{\partial y} = 0\hspace{1mm} –\hspace{1mm} 4\times 2y\hspace{1mm} –\hspace{1mm} 0$
$\dfrac{\partial F}{\partial y} = – 8y$
Now put both the partial derivative values in the implicit function theorem formula:
$f'(x) = – \dfrac{4x}{-8y}$
$f'(x) = \dfrac{4x}{8y}$
$f'(x) = \dfrac{x}{2y}$
Practice Questions:
- Find the derivative of the polynomial equation $2x^{2}\hspace{1mm}+\hspace{1mm}4y^{4}\hspace{1mm}+\hspace{1mm} 3y^{3}\hspace{1mm}+\hspace{1mm}6y^{2}\hspace{1mm}+\hspace{1mm}7y = 12$ using implicit function theorem.
- Find the derivative of the polynomial equation $2x^{5}\hspace{1mm}- \hspace{1mm}4x^{3}\hspace{1mm} +\hspace{1mm} 7 x^{2}\hspace{1mm} +\hspace{1mm}5y^{4}\hspace{1mm}+\hspace{1mm}5y^{2}\hspace{1mm}+\hspace{1mm}10y = 13$ using implicit function theorem.
- Find the derivative of the polynomial equation $6x^{4}\hspace{1mm}- \hspace{1mm}7y^{4}\hspace{1mm} + \hspace{1mm}5z^{2} = 2.sin(yz)$ using implicit function theorem.
Answer Key:
1.
First, we have to write the equation in the form $F(x,y) = 0$
$2x^{2}\hspace{1mm}+\hspace{1mm}4y^{4}\hspace{1mm}+\hspace{1mm} 3y^{3}\hspace{1mm}+\hspace{1mm}6y^{2}\hspace{1mm}+\hspace{1mm}7y = 12$
$2x^{2}\hspace{1mm}+\hspace{1mm}4y^{4}\hspace{1mm}+ 3y^{3}\hspace{1mm}+\hspace{1mm}6y^{2}\hspace{1mm}+\hspace{1mm}7y\hspace{1mm} -\hspace{1mm}12 = 0 $
The formula for implicit function theorem is given as:
$f'(x) = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}$
$\dfrac{\partial F}{\partial x} = \dfrac{\partial}{\partial x} (2x^{2}\hspace{1mm}+\hspace{1mm}4y^{4}\hspace{1mm}+ 3y^{3}\hspace{1mm}+\hspace{1mm}6y^{2}\hspace{1mm}+\hspace{1mm}7y -12)$
$\dfrac{\partial F}{\partial x} = 2\times 2x\hspace{1mm} +\hspace{1mm} 0\hspace{1mm} + \hspace{1mm}0 \hspace{1mm}+ \hspace{1mm}0 +\hspace{1mm} 0 -\hspace{1mm} 0 $
$\dfrac{\partial F}{\partial x} = 4x$
$\dfrac{\partial F}{\partial y} = \dfrac{\partial}{\partial y}(2x^{2}\hspace{1mm}+\hspace{1mm}4y^{4}\hspace{1mm}+ \hspace{1mm}3y^{3}\hspace{1mm}+\hspace{1mm}6y^{2}\hspace{1mm}+\hspace{1mm}7y -\hspace{1mm}12)$
$\dfrac{\partial F}{\partial y} = 0\hspace{1mm} +\hspace{1mm} 4\times 4y^{3} \hspace{1mm}+ \hspace{1mm}3\times 3 y^{2}\hspace{1mm}+\hspace{1mm} 6\times 2y\hspace{1mm} + \hspace{1mm}7 -\hspace{1mm}0$
$\dfrac{\partial F}{\partial y} = 16y^{3}\hspace{1mm}+ \hspace{1mm}9y^{2}\hspace{1mm}+\hspace{1mm}12y$
Now put both the partial derivative values in the implicit function theorem formula:
$f'(x) = \dfrac{4x}{16y^{3}\hspace{1mm}+ 9y^{2}\hspace{1mm}+\hspace{1mm}12y } $
2.
First we have to write the equation in the form $F(x,y) = 0$.
$2x^{5}\hspace{1mm}-\hspace{1mm} 4x^{3} \hspace{1mm}+ \hspace{1mm}7 x^{2}\hspace{1mm} +\hspace{1mm}5y^{4}+5y^{2}\hspace{1mm}+\hspace{1mm}10y = 13$
$2x^{5}\hspace{1mm}- \hspace{1mm}4x^{3}\hspace{1mm} +\hspace{1mm} 7 x^{2} \hspace{1mm}+\hspace{1mm}5y^{4}\hspace{1mm}+\hspace{1mm}5y^{2}\hspace{1mm}+\hspace{1mm}10y\hspace{1mm} -\hspace{1mm}13 = 0 $
The formula for implicit function theorem is given as:
$f'(x) = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}$
$\dfrac{\partial F}{\partial x} = \dfrac{\partial}{\partial x} (2x^{5}\hspace{1mm}-\hspace{1mm} 4x^{3}\hspace{1mm} + \hspace{1mm}7 x^{2}\hspace{1mm} +\hspace{1mm}5y^{4}\hspace{1mm}+\hspace{1mm}5y^{2}\hspace{1mm}+10y\hspace{1mm} -\hspace{1mm}13)$
$\dfrac{\partial F}{\partial x} = 2\times5 x^{4}\hspace{1mm}-\hspace{1mm} 4\times 3x^{2}\hspace{1mm}+ 7\times 2 x\hspace{1mm} +0\hspace{1mm} +\hspace{1mm} 0 +\hspace{1mm} 0 -\hspace{1mm} 0 $
$\dfrac{\partial F}{\partial x} = 10x^{4}- 12x^{2}+14x$
$\dfrac{\partial F}{\partial y} = \dfrac{\partial}{\partial y}(2x^{5}- 4x^{3} + 7 x^{2} +5y^{4}+5y^{2}+10y -13)$
$\dfrac{\partial F}{\partial y} = 0 \hspace{1mm}–\hspace{1mm} 0 \hspace{1mm}+ \hspace{1mm}0 +\hspace{1mm} 5\times 4y^{3}\hspace{1mm}+\hspace{1mm}5\times 2y \hspace{1mm}+\hspace{1mm}10 \hspace{1mm}- \hspace{1mm}0$
$\dfrac{\partial F}{\partial y} = 20y^{3}\hspace{1mm}+\hspace{1mm}10y \hspace{1mm}+ \hspace{1mm}10$
Now put both the partial derivative values in the implicit function theorem formula:
$f'(x) = \dfrac{10x^{4}\hspace{1mm}-\hspace{1mm} 12x^{2}\hspace{1mm}+\hspace{1mm}14x }{20y^{3}\hspace{1mm}+\hspace{1mm}10y \hspace{1mm}+ 10 }$
$f'(x) = \dfrac{5x^{4}\hspace{1mm}-\hspace{1mm} 6x^{2}\hspace{1mm}+\hspace{1mm}7x }{10y^{3}\hspace{1mm}+\hspace{1mm}5y \hspace{1mm}+\hspace{1mm} 5) } $
3.
First, we have to write the equation in the form $F(x,y,z) = 0$.
$6x^{4}\hspace{1mm}- \hspace{1mm}7y^{4} \hspace{1mm}+\hspace{1mm} 5z^{2} = 2.sin(yz)$
$6x^{4}\hspace{1mm}-\hspace{1mm} 7y^{4} \hspace{1mm}+\hspace{1mm} 5z^{2}\hspace{1mm} – 2.sin(yz) = 0$
The formulas for implicit function theorem for three variables are given as:
$\dfrac{\partial z}{\partial x} = – \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$
$\dfrac{\partial z}{\partial y} = – \dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
$\dfrac{\partial F}{\partial x} = \dfrac{\partial}{\partial x}(6x^{4}- 7y^{4} + 5z^{2} – 2.sin(yz))$
$\dfrac{\partial F}{\partial x} = 6\times 4x^{3}\hspace{1mm} -\hspace{1mm} 0 \hspace{1mm}+ \hspace{1mm}0\hspace{1mm} -\hspace{1mm} 0$
$\dfrac{\partial F}{\partial x} = 24x^{3}$
$\dfrac{\partial F}{\partial y} = \dfrac{\partial}{\partial y}(6x^{4}\hspace{1mm}- \hspace{1mm}7y^{4} \hspace{1mm}+ \hspace{1mm}5z^{2} – 2.sin(yz)) $
$\dfrac{\partial F}{\partial y} = 0\hspace{1mm} –\hspace{1mm} 7\times 4y^{3}\hspace{1mm} +\hspace{1mm} 0 –\hspace{1mm} 2z.cos(yz) $
$\dfrac{\partial F}{\partial y} = – 28y^{3}\hspace{1mm} – \hspace{1mm}2z.cos(yz)$
$\dfrac{\partial F}{\partial y} = -2 (14y^{3}\hspace{1mm}+\hspace{1mm} z.cos(yz))$
$\dfrac{\partial F}{\partial z} = \dfrac{\partial}{\partial z}(6x^{4}\hspace{1mm}- \hspace{1mm}7y^{4}\hspace{1mm} +\hspace{1mm} 5z^{2} – \hspace{1mm}2.sin(yz))$
$\dfrac{\partial F}{\partial z} = 0\hspace{1mm} –\hspace{1mm} 0 +\hspace{1mm}5\times 2z – 2y.cos(yz) \dfrac{\partial F}{\partial z} = 10z\hspace{1mm} –\hspace{1mm} 2ycos(yz)$
$\dfrac{\partial F}{\partial z} = 2(5z – y.cos(yz))$
Now put both the values in the formulas to get the final answer:
$\dfrac{\partial z}{\partial x} $= $- \dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$
$\dfrac{\partial z}{\partial x} = – \dfrac{24x^{3}}{2(5z\hspace{1mm} –\hspace{1mm} y.cos(yz))}$
$\dfrac{\partial z}{\partial x} = – \dfrac{12x^{3}}{(5z\hspace{1mm} –\hspace{1mm} y.cos(yz))}$
$\dfrac{\partial z}{\partial y} = – \dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
$\dfrac{\partial z}{\partial y} = – \dfrac{-2 (14y^{3}\hspace{1mm}+\hspace{1mm} z.cos(yz))}{ 2(5z\hspace{1mm} –\hspace{1mm} y.cos(yz))}$
$\dfrac{\partial z}{\partial y} = \dfrac{ (14y^{3}\hspace{1mm}+ \hspace{1mm} z.cos(yz))}{(5z\hspace{1mm} – \hspace{1mm}y.cos(yz))}$
