JUMP TO TOPIC
 Indirect measurement is a method of measuring a thing or an object by using alternative methods of measurement instead of measuring it directly.
Indirect measurement is a method of measuring a thing or an object by using alternative methods of measurement instead of measuring it directly.
Indirect measurements are different from direct measurements and are mostly applied or used when direct measurement is not possible. It can be done by using the Pythagorean theorem, similar triangles, and proportions.
This topic will help you understand the concept of indirect measurement and how to use it, as well as cover multiple numerical examples so that you can grasp the concept quickly.
What Is Indirect Measurement?
Indirect measurement is a method that is used in scenarios where direct measurement is not possible. These methods can be used to measure the width of the river and the height of an object using its shadow or other available measurements.
Indirect measurement in surveying is another example. Basically, we will model the given scenario in the form of triangles and then calculate the desired value using proportions, similar triangles, and the Pythagorean theorem.
For example, you want to measure the height of a tree but you do not have the tools to measure the height of the tree directly. In such a scenario, you will have to measure the height of the tree indirectly.
We can measure the height of the tree by standing next to it while using indirect measurement methods such as a mirror or the shadow of the tree. Both methods need the presence of sunlight, otherwise, both of these methods won’t work. Let us discuss both of these methods in detail.
Suppose a person is standing in front of the tree while a mirror is placed on the ground in between them.
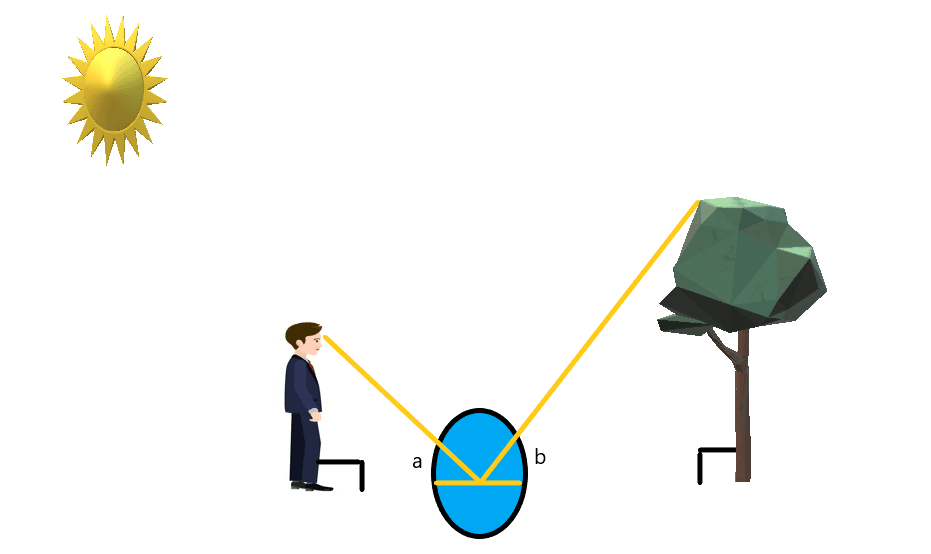
The person is standing in such a way that he or she can easily see the tip of the tree. If the person is looking at the mirror, then by using the reflection property of the light and a mirror we can create a concurrent angle at each side of the mirror.
If we assume the person is standing straight and the tree is also straight like an arrow, then we can assume that both are standing at $90^{o}$ angle. We can create similar triangles for this case and then solve for the height of the tree.
Let’s continue with the same example, but this time we will use the shadow of the person and the tree to generate similar triangles.

Suppose a person is standing in front of the tree while the sun is out and if we assume the angle of the sun remains constant, then the shadow cast by the person and the tree can be used to draw similar triangles.
If we assume the person and tree are standing straight at an angle of $90^{o}$ and if we draw a line from the top of the tree and the person to the end of their shadows, then it gives us two similar triangles.
Indirect Measurement Techniques
There are several techniques that can be used to solve problems where direct measurement is not possible.
Pythagorean Theorem
The Pythagorean or Pythagoras theorem is a theorem that is used to formulate a relation between three sides of a right-angle triangle. According to the Pythagorean theorem, if a right angle triangle is given, then the relation for the three sides of the triangle can be given as:
$c^{2}= a^{2}+ b^{2}$
The Pythagorean theorem can be used as an indirect measurement technique.
For example, we want to estimate the length of the bridge that needs to be built across a river. If we know the distance across the river and the height of the land on the higher side of the river, then the bridge will be like a hypotenuse in a right-angle triangle. If the distance across the river is $20$ meters and the height of the bank (on the higher side of the river ) is $5$ meters, then the length of the bridge can be calculated as:
$c^{2} = b^{2} + c^{2}$
$c^{2} = 20^{2} + 5^{2}$
$c^2 = 400 + 25 = 425$
$c = \sqrt {425} \cong 20.62$ meters.
Similar Triangles and Proportionality
Similar triangles’ properties are extensively used in solving problems via indirect measurement. Two triangles are said to be similar if their corresponding angles are similar or concurrent.
The shapes of both triangles are similar while the size of the triangles may vary. If we can draw two similar triangles for a given problem, then we can find the missing data of the triangles by using the proportions method.
Similar triangles and proportionality can simply be named as triangle proportionality theorem. Let us study a simple example of triangle proportionality.
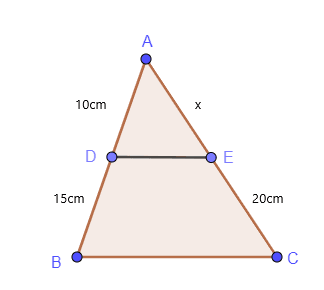
$\dfrac{AD}{DB} = \dfrac{AE}{EC}$
$\dfrac{10}{15} = \dfrac{x}{20}$
$x = \dfrac{2\times 20}{3}$
$x = \dfrac{40}{3}$cm
Let us now study various direct and indirect measurement examples.
Example 1:
Allan has a tree outside his house, but he cannot measure its height directly as the tree is quite high, so you are required to help Allan to determine the height of the tree. During this time of the day, the shadow of the tree is $150$ ft while the shadow of Allan (if he stands in front of the tree) is $5$ ft. If Allan is $4$ ft tall, what is the height of the tree?
Solution:
We are taking the length of both shadows at the same time, so the angle of the sun will remain constant and if the tree and Allan are making an angle of $90^{o}$ i.e they are standing dead straight vertically, then we can assume that Allan is standing parallel to the tree and we will have two similar triangles.
Let “$x$” be the height of the tree, then by using the triangle proportionality theorem we can write:
$\dfrac{4 ft}{x} = \dfrac{5}{150}$
$\dfrac{4 ft}{x} = \dfrac{1}{30}$
$x = 4 \times 30 = 120$ ft
Example 2:
Sana has a pole outside her house that she wants to measure the length of, but she cannot measure it directly. You are required to help Sana out in the calculation of the height of the pole using the mirror method.
Sana is $1.8$ meters tall and she can see the top of the pole if she places the mirror on the ground while standing $5$ meters away from the mirror. The mirror is $35$ meters away from the pole. What is the height of the pole?
Solution:
If we assume that both the pole and Sana are standing at $90^{o}$ angle, then the reflection of the mirror will create triangles having congruent angles. Hence, two similar triangles are created and we can use the triangle proportionality theorem to determine the height of the pole.
Let “$x$” be the height of the pole, then by using the triangle proportionality theorem we can write:
$\dfrac{35 m}{5 m} = \dfrac{x}{1.8 m}$
$7 = \dfrac{x}{1.8 m}$
$x = 1.8 \times 7 = 12.6$ meter
Example 3:
A building casts a shadow that is $35$ meters long while at the same time a man standing parallel to the building casts a shadow that is $4.5$ meters long. If the man is $4$ meters tall, what is the height of the building?
Solution:
$\dfrac{35 m}{4.5 m} = \dfrac{x}{4 m}$
$7.7 = \dfrac{x}{4 m}$
$x = 4 \times 7.7 = 31$ meter approx.
Example 4:
Nancy is playing basketball on the basketball court outside her house. Nancy knows she is $5$ ft tall and she is casting a shadow that is $5.5$ ft tall while the hoop of the basketball is $10$ ft tall. What is the length of the shadow of the basketball hoop?
Solution:
Let “x” be the length of the shadow of the hoop, then by using the triangle proportionality theorem we can write:
$\dfrac{5 ft}{5.5 ft} = \dfrac{10 ft}{x}$
$0.909 = \dfrac{10}{x}$
$x = \dfrac{10}{0.909} = 11$ ft approx.
Practice Questions:
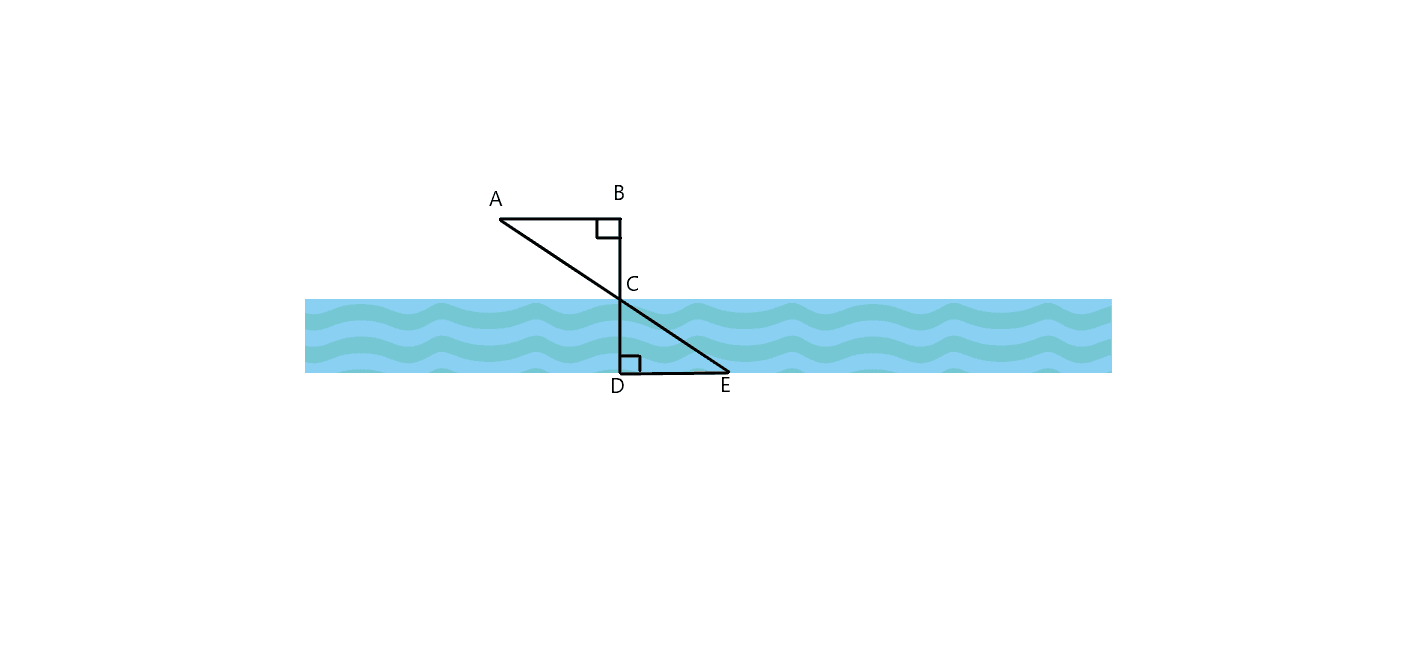
1. For the picture given below, is the $\triangle ABC \cong \triangle EDC$? How is $AB$ parallel to $DE$? If both the triangles are similar, then calculate the width of the river if $AB = 25$ ft, $BC = 30$ ft, and $DE = 60$ ft.
2. A tree casts a shadow that is $40$ ft long, while at the same time a man standing parallel to the tree casts a shadow that is $5$ ft long. If the man is $4.5$ ft tall, what is the height of the tree?
Answer Key:
1.
$\triangle ABC$ is concurrent to $\triangle EDC$. As angle B and angle D, both are right angles while $\angle ABC \cong \angle ECD$ as both are vertical angles and hence, by A. A similarity postulates both these triangles are called similar triangles.
As both the triangles are similar and by A. A postulate $\angle ABC \cong \angle ECD$, if the alternate interior angles are congruent to each other then the corresponding line segments are parallel to each other. Hence, $AB || DE$.
The width of the river is can be determined by calculating the length of the CD. We can do that by using the triangle proportionality theorem.
$\dfrac{30 ft}{CD} = \dfrac{25}{60}$
$CD = 72$ ft.
2.
$\dfrac{40 ft}{5 ft} = \dfrac{x}{4.5 ft}$
$8 = \dfrac{x}{4.5 ft}$
$x = 4.5 \times 8 = 36$ ft.
