JUMP TO TOPIC
 To find the area of the shaded region of a circle, we need to know the type of area that is shaded.
To find the area of the shaded region of a circle, we need to know the type of area that is shaded.
The general rule to find the shaded area of any shape would be to subtract the area of the more significant portion from the area of the smaller portion of the given geometrical shape. Still, in the case of a circle, the shaded area of the circle can be an arc or a segment, and the calculation is different for both cases.
This guide will provide you with good-quality material that will help you understand the concept of the area of the circle. At the same time, we will discuss in detail how to find the area of the shaded region of the circle using numerical examples.
What Is the Area of the Sector of a Circle?
The area of the sector of a circle is basically the area of the arc of a circle. The combination of two radii forms the sector of a circle while the arc is in between these two radii.
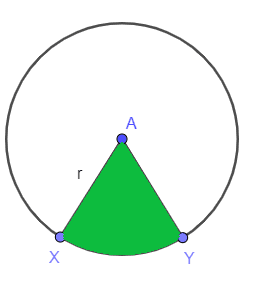
Consider the figure below; you are asked to find the area of the shaded sector of a circle. The radius of the circle is shown as “$r$” while “$XY$” is the arc and it is bounding the sector, thus the area of the sector is given as:
Area of the sector = $\dfrac{mXY}{360^{o}}. \pi r^{2}$
Example 1:
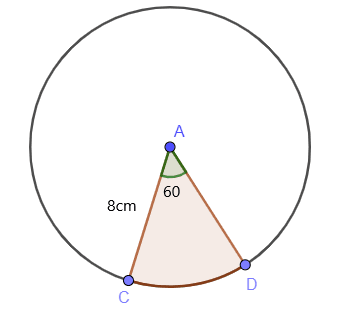
Find the area of the shaded region of a circle by using the area formula of the sector if the value of the radius is $8$cm and \theta is $60^{o}$.
Solution:
The central angle of the arc /sector, as we can see from the figure, is $60^{o}$. So, we know that the area of the shaded sector can be calculated as:
Area of the sector = $\dfrac{60^{o}}{360^{o}}. \pi r^{2}$
Area of the sector = $\dfrac{1}{6}. \pi 8^{2}$
Area of the sector = $\dfrac{1}{6}. 3.1416. 64 = 33.5 cm^{2}$
Example 2:
Suppose the area of the sector of a circle is $50 cm^{2}$ while the central angle of the circle is $30^{o}$. What will be the value of the radius of the circle?
Solution:
We are given the area and central angle of the sector, so we can find the radius of the sector by using the formula of the area of the sector.
Area of the sector = $\dfrac{\theta}{360^{o}}. \pi r^{2}$
$50 = \dfrac{30^{o}}{360^{o}}. \pi r^{2}$
$50 = \dfrac{1}{12}. 3.1416 . r^{2}$
$600 = 3.1416 . r^{2}$
$r^{2} = 191$
$r = 13.82$ cm
Example 3:
Suppose the area of the sector of a circle is $9\pi cm^{2}$ while the radius of the circle is $8$ cm. What will be the central angle of the sector?
Solution:
We are given the area and the radius of the sector, so we can find the central angle of the sector by using the formula of the area of the sector.
Area of the sector = $\dfrac{\theta}{360^{o}}. \pi r^{2}$
$9\pi = \dfrac{\theta }{360^{o}}. \pi 8^{2}$
$9\pi = \dfrac{\theta }{360^{o}}. \pi 64$
$9 = \dfrac{8\theta }{45^{o}}$
$\theta = \dfrac{9 \times 45^{o}}{8}$
$\theta = 50.62^{o}$
Example 4:
If the area of the sector of a circle is $60\pi cm^{2}$ while the arc length of the circle is $10\pi$, what will be the radius and central angle of the circle?
Solution:
We are given the arc length of the circle and an arc length is a fraction/part of the circumference of the circle.
The formula for the arc length of a circle is:
Arc length = $\dfrac{\theta}{360^{o}}. 2\pi r$
$10 = \dfrac{\theta}{360^{o}}. 2 r$
$5 = \dfrac{\theta}{360^{o}}. R$ (1)
Likewise, we are also given the area of the sector of the circle and the formula for the area of the sector is given as:
Area of the sector = $\dfrac{\theta}{360^{o}}. \pi r^{2}$
$60\pi = \dfrac{\theta}{360^{o}}. \pi r^{2}$
$60 = \dfrac{\theta}{360^{o}}. r^{2}$ (2)
Using the substitution method to solve for the radius and central angle of the circle by using equation (1) and (2), we can now substitute the value of arc length in the formula of the area of the sector. Afterwards, we can solve for the radius and central angle of the circle.
$60 = \dfrac{\theta}{360^{o}}. r^{2} = 60 = \dfrac{\theta}{360^{o}}. r .r$
$60 = 5r$
$r = \dfrac{60}{5}= 30$ cm
We can now solve for the central angle by using equation (1)
$5 = \dfrac{\theta}{360^{o}}. r$
$1800 = \theta . 30$
$\theta = \dfrac{1800}{30} = 60^{o}$
What Is the Area of the Segment of a Circle?
The area of the circle enclosed in a segment or the shaded region inside the segment is known as the area of the segment of a circle. A segment is an interior part of the circle. If we draw a chord or a secant line, then the blue area as shown in the figure below, is called the area of the segment.
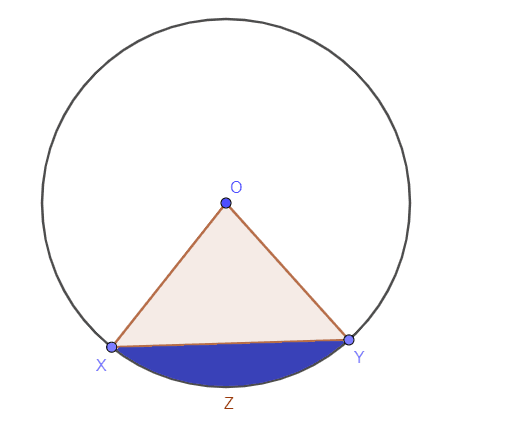
There are two types of circle segments:
- minor segment
- major segment
The primary difference between the minor and major segments is that the major segment has a greater area compared to the minor segment.
The formula to determine the area of the shaded segment of the circle can be written as radians or degrees.
Area of segment of a circle (Radians) = $\dfrac{1}{2}. r^{2}(\theta – sin\theta)$
Area of segment of a circle (Radians) = $\dfrac{1}{2}. r^{2}((\dfrac{\pi}{180})\theta – sin\theta)$
How To Determine the Area of a Segment of a Circle
The calculation required to determine the area of a segment of a circle is a bit tricky, as you need to have a good grasp of finding the areas of a triangle. The picture in the previous section shows that we have a sector and a triangle.
To determine the area of the segment, we first need to calculate the area of the segment, which is XOYZ ( A_XOYZ), and after that, we have to calculate the area of the triangle $\ triangle \triangle XOY$.
To calculate the area of the segment, we need to subtract the area of the sector from the area of the triangle. We have already discussed how to calculate the area of the sector, while you can learn in detail how to calculate the area of a triangle. With this, we can write the formula for the area of the segment XYZ as:
Area of the segment = Area of the sector – Area of the triangle
Where,
Area of sector = $\dfrac{\theta}{360^{o}}. \pi r^{2}$
Area of triangle = $\dfrac{1}{2} \times base \times height$
Example 5:
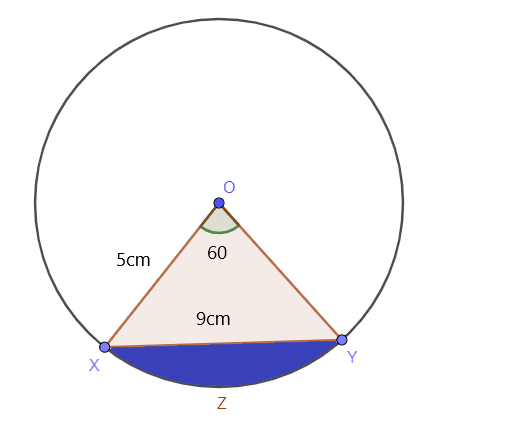
Determine the area of the shaded segment of the circle while the central angle of the circle is $60^{o}$ and the radius of the circle is $5$ cm while the length of the XY is $9$ cm, as shown in the picture below:
Solution:
Area of the sector = $\dfrac{\theta}{360^{o}}. \pi r^{2}$
Area of the sector = $\dfrac{60^{o}}{360^{o}}. \pi 5^{2}$
Area of the sector = $\dfrac{1}{6}. 3.1416 . 25$
Area of the sector = $13.09 cm^{2}$
To determine the area of the triangle, we have to calculate the length of the side OM by using the Pythagorean theorem.
OM = $\sqrt{r^{2}-(\dfrac{XM}{2}XM)^{2}}$
OM = $\sqrt{5^{2}- 4.5^2 }$
OM = $\sqrt{4.75} = 2.2$
Area of the triangle = $\dfrac{1}{2} \times OM \times XY$
Area of the triangle = $\dfrac{1}{2} \times 2.2 \times 9$
Area of the triangle = $9.9 = 10 cm^{2}$
Area of the segment = $13.09 -10 = 3.09 cm^{2}$
Example 6:
Consider the exact figure as in example 5. Find the area of the shaded segment of the circle while the central angle of the circle is $60^{o}$ and the radius of the circle is $7$ cm, as shown in the picture (the value of line segment XY is unknown).
Solution:
The blue area of the circle is basically the area of the sector, and it can be calculated as:
Area of the sector = $\dfrac{\theta}{360^{o}}. \pi r^{2}$
Area of the sector = $\dfrac{60^{o}}{360^{o}}. \pi 7^{2}$
Area of the sector = $\dfrac{1}{6}. 3.1416 . 49$
Area of the sector = $25.65 cm^{2}$
To determine the area of the triangle, we have to calculate the length of the side OM, and as the length of XM is not given, we cannot use the Pythagorean theorem. Instead, we can find the value of OM as:
Area of the triangle = $\dfrac{1}{2} \times OM \times XY$
OM = $r cos( \dfrac{\theta}{2})$
OM = $7 \times cos(30)$
OM = $7 \times \dfrac{\sqrt{3}}{2}$
OM = $6.06 cm$
XY = $2\times YM = 2\times 7 \times sin 30$
XY = $7$
Area of the triangle = $\dfrac{1}{2} \times 6.06 \times 7$
Area of the triangle = $21.21 cm^{2}$
Area of the segment = $25.65 – 21.21 = 4.44 cm^{2}$
The Area of a Circular Shaded Portion of a Circle
We can calculate the area of a shaded circular portion inside a circle by subtracting the area of the bigger/larger circle from the area of the smaller circle. Consider the picture below.
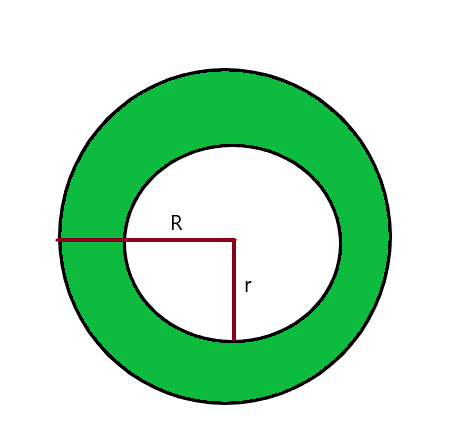
Area of the smaller circle A = $\pi r^{2}$
Area of the bigger circle B = $\pi R^{2}$
Area of the shaded circular region = Area of circle A – Area of circle B
Area of the shaded circular region = $\pi R^{2} – \pi r^{2}$ = $\pi ( r^{2}- R^{2})$
Lets say if $R = 2r$, then the area of the shaded region would be:
Area of shaded region = Area of circle A – Area of circle B = $\pi (2r)^{2} – \pi r^{2}$
Area of shaded region = $4\pi r^{2} – \pi r^{2} = 3 \pi r^{2}$
The area of the circular shaded region can also be determined if we are only given the diameter of the circle by replacing “$r$” with “$2r$”.
Example 7:
Find the area of the shaded region in terms of pi for the figure given below.
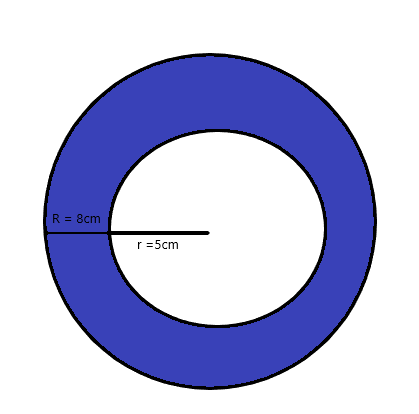
Solution:
The radius of the smaller circle is = $5$ cm
The radius of the larger/bigger circle is = $8$ cm
Area of the shaded circular region = Area of circle A – Area of circle B
Area of the shaded circular region = $\pi R^{2} – \pi r^{2}$
Area of the shaded circular region = $\pi 8^{2} – \pi 5^{2}$
Area of the shaded circular region = $\pi (64 – 25) = 39\pi$.
Hopefully, this guide helped you develop the concept of how to find the area of the shaded region of the circle. As you saw in the section on finding the area of the segment of a circle, multiple geometrical figures presented as a whole is a problem. This topic will come in handy during times like these.
- To determine the area of the shaded region of a triangle.
- To determine the area of the shaded region of a square.
- To determine the area of the shaded region of a rectangle.
Conclusion
We can conclude that calculating the area of the shaded region depends upon the type or part of the circle that is shaded.
- If the shaded region of the circle is in the form of a sector, then we will calculate the area of the sector by using the formula: Area of the sector = $\dfrac{mXY}{360^{o}}. \pi r^{2}$.
- Suppose the shaded region is the segment of a circle. In that case, we can calculate the area of the segment of the circle by using the formula Area of segment = Area of the sector – Area of a triangle.
- If the shaded region is in the form of a circle, then we can calculate the shaded region’s area by subtracting the larger circle’s area from the area of the smaller circle.
So finding the area of the shaded region of the circle is relatively easy. All you have to do is distinguish which portion or region of the circle is shaded and apply the formulas accordingly to determine the area of the shaded region.
