JUMP TO TOPIC

Triangular pyramids are captivating geometrical structures that offer a delightful fusion of elegance and mathematical precision. As a cornerstone of three-dimensional geometry, this shape boasts a range of intriguing properties and carries extensive applications across diverse fields. The triangular pyramid, often referred to as a tetrahedron, consists of four triangular faces, four vertices, and six edges, all merging to form a structure that has captivated mathematicians, architects, and artists alike throughout history.
In this exploration of the triangular pyramid, we’ll delve into its definition, properties, related formulas, mathematical examples, and real-world applications, painting a comprehensive picture of this intriguing geometric shape.
Definition
A triangular pyramid, also known as a tetrahedron, is a three-dimensional geometric shape that is a type of pyramid. It is defined by four triangular faces that converge to a single point, known as the apex. These faces enclose a volume in space and form a base that is itself a triangle. The triangular pyramid has four vertices, where the edges meet, and six edges in total.
The shape has a base formed by a triangle rather than a square or other polygon, distinguishing it from other types of pyramids. It is one of the simplest and most basic polyhedra, making it a foundational shape in geometry. Below we present a generic geometric diagram for the triangular pyramid.
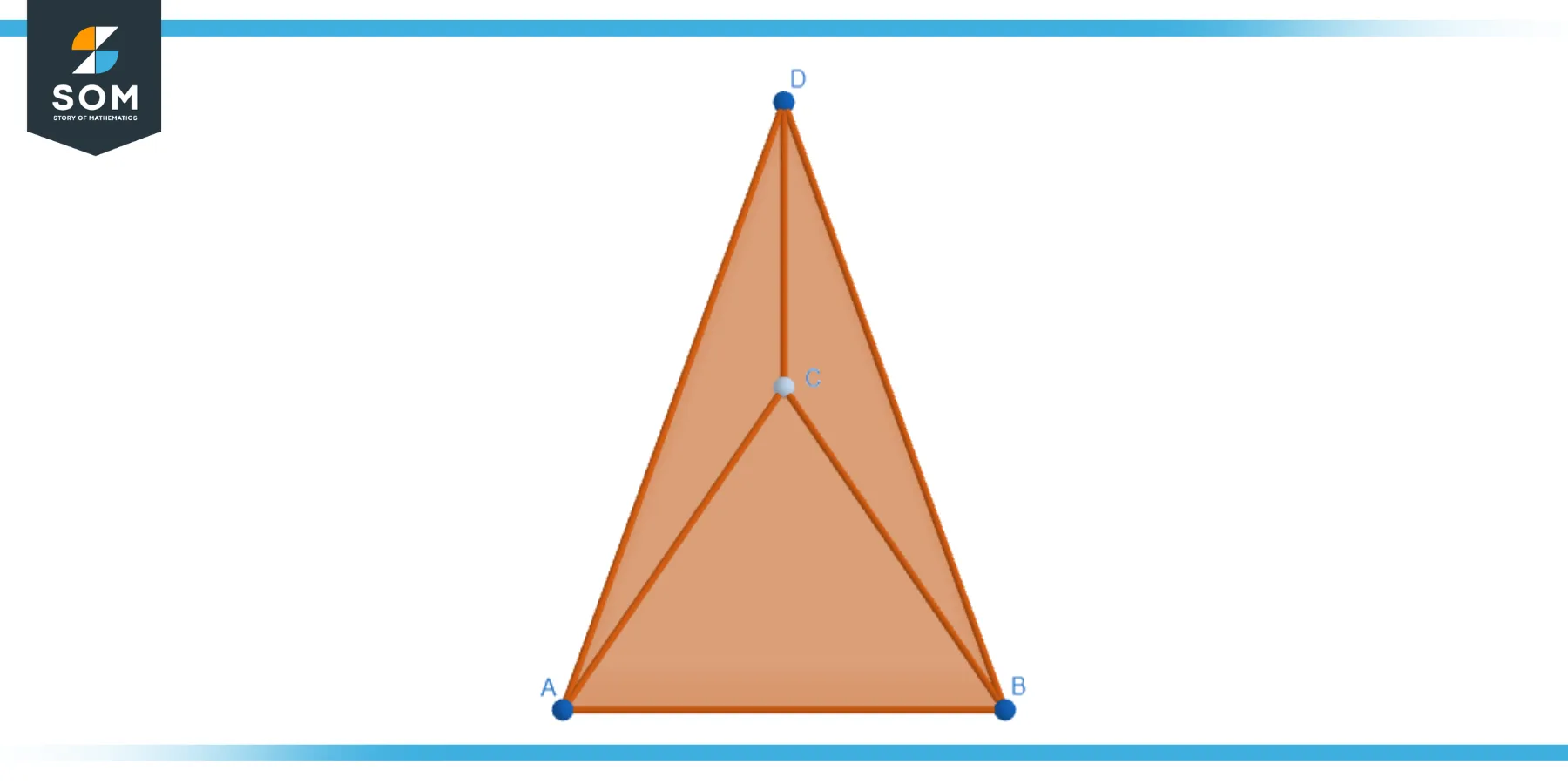
Unlike other pyramids, the triangular pyramid is unique in that all its faces are the same shape – triangles. It’s also noteworthy for being the simplest type of pyramid that can exist in three dimensions.
Historical Significance
The triangular pyramid, also known as a tetrahedron, holds a rich historical background that spans ancient civilizations. Exploring its origins provides insights into the development of geometry and its practical applications.
The study of geometry can be traced back to ancient civilizations, where foundational geometric principles were established. The concept of the triangular pyramid gained prominence during the time of the ancient Greeks, who significantly improved the science of mathematics.
Greek mathematicians, including Euclid and Pythagoras, explored the properties and characteristics of various geometric shapes, including the triangular pyramid. Euclid’s influential work, “Elements,” compiled around 300 BCE, presented a comprehensive treatise on geometry, encompassing the study of polyhedra, such as the tetrahedron.
However, the understanding and use of triangular pyramids extend beyond ancient Greece. Ancient Egyptian and Mesopotamian cultures also incorporated pyramidal structures into their architecture, focusing primarily on square-based pyramids rather than triangular ones.
The triangular pyramid, associated with religious and mystical beliefs, gained symbolic and cultural significance in ancient Egypt. The pyramids of Egypt, such as the Great Pyramid of Giza, showcased the Egyptians’ advanced knowledge of mathematics and engineering, which they utilized to construct impressive triangular pyramids as tombs for their pharaohs.
In modern times, the study of triangular pyramids and polyhedra continues to be a subject of mathematical exploration. Mathematicians delve into the properties, surface area, volume, and spatial relationships of triangular pyramids, further expanding our understanding of geometric principles.
Furthermore, the triangular pyramid has found practical applications beyond mathematics. Architects and engineers leverage its stable structure and aesthetic appeal in various fields, including architecture, construction, and design. The tetrahedral shape is employed to construct bridges, trusses, space frames, and even architectural forms.
The historical background of the triangular pyramid highlights its enduring significance as a fundamental geometric shape. From ancient civilizations to modern applications, the triangular pyramid exemplifies the intersection of mathematics, architecture, and engineering. It’s geometric properties and cultural symbolism have left a lasting legacy, shaping our understanding of geometry and its diverse practical applications.
Types
The triangular pyramid primarily comes in two main types based on the nature of its faces:
Regular Triangular Pyramid (Tetrahedron)
A regular triangular pyramid, also referred to as a tetrahedron, is a type of triangular pyramid in which all four faces are equilateral triangles. This means that all edges are of equal length, and all angles are equal. The regular tetrahedron is the simplest of all polyhedra and is a Platonic solid. Below we present a generic diagram for the regular triangular pyramid.
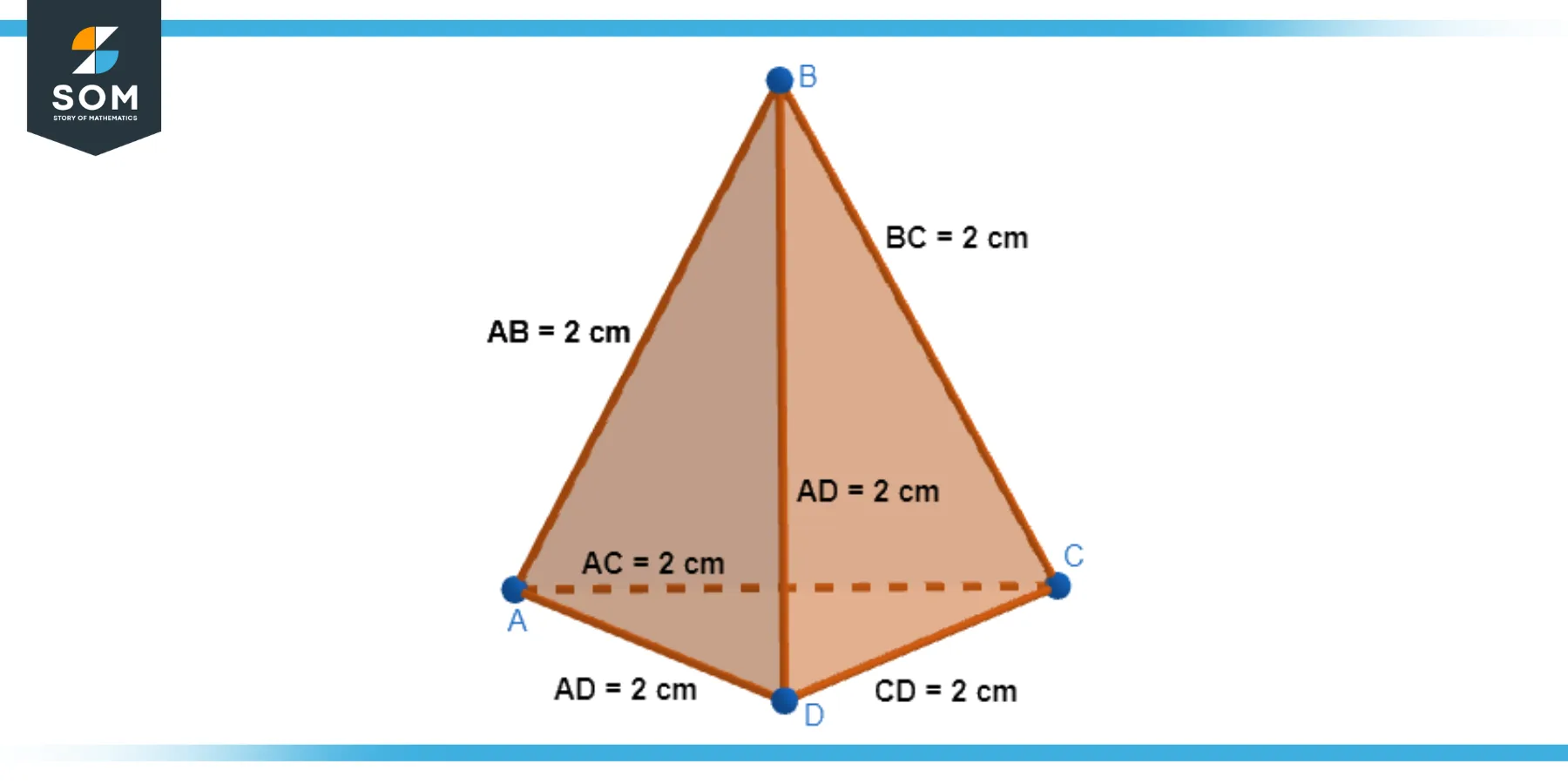
Figure-2: Regular triangular pyramid.
Irregular Triangular Pyramid
A pyramid having a triangle base and three triangular faces that don’t all have the same edge lengths or angles is referred to as an irregular triangular pyramid. The triangles can be of any variety (scalene, isosceles, or equilateral), and the apex does not necessarily align vertically with the centroid of the base. Below we present a generic diagram for the irregular triangular pyramid.
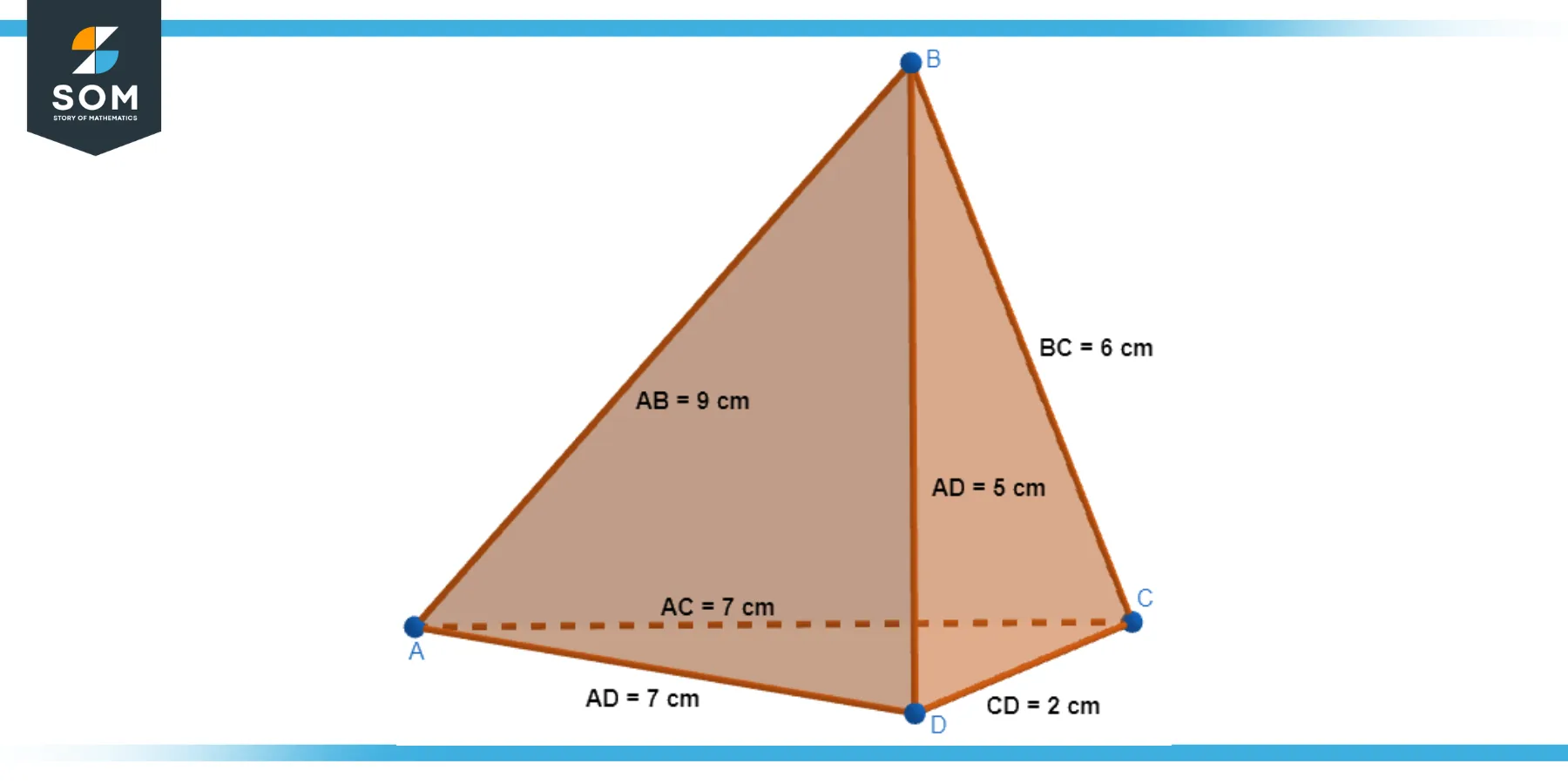
Figure-3: Irregular triangular pyramid.
Each type has its unique set of properties and uses, but they both share the same basic structure of a pyramid with a triangular base. The differentiation between regular and irregular allows for a broad range of applications and potential for various mathematical problems and real-world scenarios.
Properties
The triangular pyramid, also known as a tetrahedron, has several intriguing geometric properties that make it a fascinating topic in three-dimensional geometry. Here are the key properties:
Faces
A triangular pyramid has four faces. Each face is a triangle. In a regular triangular pyramid or tetrahedron, all four faces are equilateral triangles.
Edges
A triangular pyramid has six edges. In a regular triangular pyramid, all the edges are of equal length.
Vertices
A triangular pyramid has four vertices. In a regular triangular pyramid, the distance between any two vertices is the same.
Base and Apex
One face of the pyramid serves as the base, and the opposite vertex is known as the apex. The line joining the apex and the centroid of the base is called the height of the pyramid.
Slant Height
The slant height is the distance from the apex to the edge of the base. In a regular triangular pyramid, all slant heights are equal.
Angles
In a regular triangular pyramid, each face forms an angle of 60 degrees with adjacent faces, and the angle between a base edge and a side edge is approximately 70.53 degrees.
Volume and Surface Area
The calculations for a triangular pyramid’s volume and surface area entail the base area, slant height, and height of the pyramid. For a regular triangular pyramid, these formulas simplify to functions of the edge length alone.
Symmetry
A regular triangular pyramid has tetrahedral symmetry, one of the most basic forms of three-dimensional symmetry. This means it looks the same when rotated about any axis passing through a vertex and the centroid of the opposite face.
Euler’s Formula
A triangular pyramid follows Euler’s Formula for polyhedra: Faces + Vertices – Edges = 2. For a triangular pyramid, this is 4 + 4 – 6 = 2.
These properties make the triangular pyramid an essential geometric shape in various fields, from mathematics and physics to engineering and computer graphics.
Ralevent Formulas
The triangular pyramid, or tetrahedron, is associated with a number of key formulas related to its dimensions and geometric properties. Here, we’ll discuss the primary formulas involved:
Volume (V)
The volume of a triangular pyramid is given by the formula:
V = 1/6 × Base Area × Height
This formula states that the volume is equal to one-sixth of the product of the base area and the height (the perpendicular distance from the base to the apex).
Surface Area (A)
A triangular pyramid’s total surface area is equal to the sum of each of its triangle sides. The formula for the surface area is:
A = Base Area + 1/2 × Perimeter of Base × Slant Height
Here, the slant height is the height of one of the triangular faces or the distance from the base to the apex along the face of the pyramid.
For a regular tetrahedron (where all edges are of equal length a):
Volume (V) = a³ / (6 × √(2))
Surface Area (A) = √(3) × a²
Height (h)
The height of a triangular pyramid is found by the Pythagorean theorem if the slant height (l) and the edge length of the base (a) are known in a regular tetrahedron:
h = √(l² – a²/4)
The aforementioned formulas play a critical role in many mathematical and practical applications, aiding in the computation of key attributes related to the triangular pyramid.
Applications
The triangular pyramid, also known as a tetrahedron, finds versatile applications across various fields due to its unique geometric properties. Let’s explore some key areas where it is applied.
Architecture and Structural Design
The triangular pyramid serves as a foundational element in architectural design and structural engineering. Its stable and self-supporting structure makes it suitable for constructing towers, roofs, and other architectural components. The triangular pyramid’s geometry allows for efficient load distribution and structural stability, making it a preferred choice in various architectural designs.
Mathematics and Geometry Education
The triangular pyramid plays a crucial role in mathematics education, particularly in the study of polyhedra and spatial geometry. It helps students understand concepts such as vertices, edges, faces, volume, and surface area. By exploring the properties of the triangular pyramid, students develop a deeper understanding of geometric principles and enhance their spatial reasoning skills. The hands-on exploration and visualization of the triangular pyramid contribute to a comprehensive understanding of three-dimensional geometry.
Molecular Geometry and Chemistry
In the field of chemistry, the triangular pyramid represents the molecular geometry of certain compounds. It helps determine the spatial arrangement of atoms and predict molecular properties and behavior.
Computer Graphics and 3D Modeling
The triangular pyramid is a fundamental shape used in computer graphics and 3D modeling. It forms the basis for creating complex 3D objects, virtual environments, and simulations.
Crystallography and Material Science
The triangular pyramid is relevant in crystallography, where it represents the crystal structure of certain minerals and compounds. Understanding the arrangement of atoms within a tetrahedral lattice is crucial in studying material properties.
Network Topology and Graph Theory
The triangular pyramid is used to model and analyze network topologies and connections in graph theory. It represents interconnected nodes or vertices, with edges connecting each vertex to the others.
Engineering and Construction
The triangular pyramid’s stable geometry and load-bearing capacity make it useful in engineering applications. It is employed in truss structures, space frames, and even bridge design to provide structural strength and stability.
Geometric Art and Sculpture
Artists and sculptors often incorporate the aesthetic appeal of the triangular pyramid into their works. It serves as a visually intriguing shape, lending itself to modern art installations, sculptures, and geometric patterns.
Graph Theory
Tetrahedrons can represent the simplest non-planar graph, which is a core concept in graph theory and computer science.
Ecology
In models of ecological systems, tetrahedrons can represent a simple system with four elements interacting with each other.
The triangular pyramid‘s applications extend beyond these examples, highlighting its broad utility across multiple fields. Its geometric properties, stability, and aesthetic appeal make it a valuable shape in architecture, mathematics, engineering, and artistic endeavors. The versatility of the triangular pyramid continues to inspire innovation and creativity in diverse areas of study and practice.
Exercise
Example 1
Finding the Volume of a Triangular Pyramid Given
For the given triangular pyramid in Figure-4, find its volume.
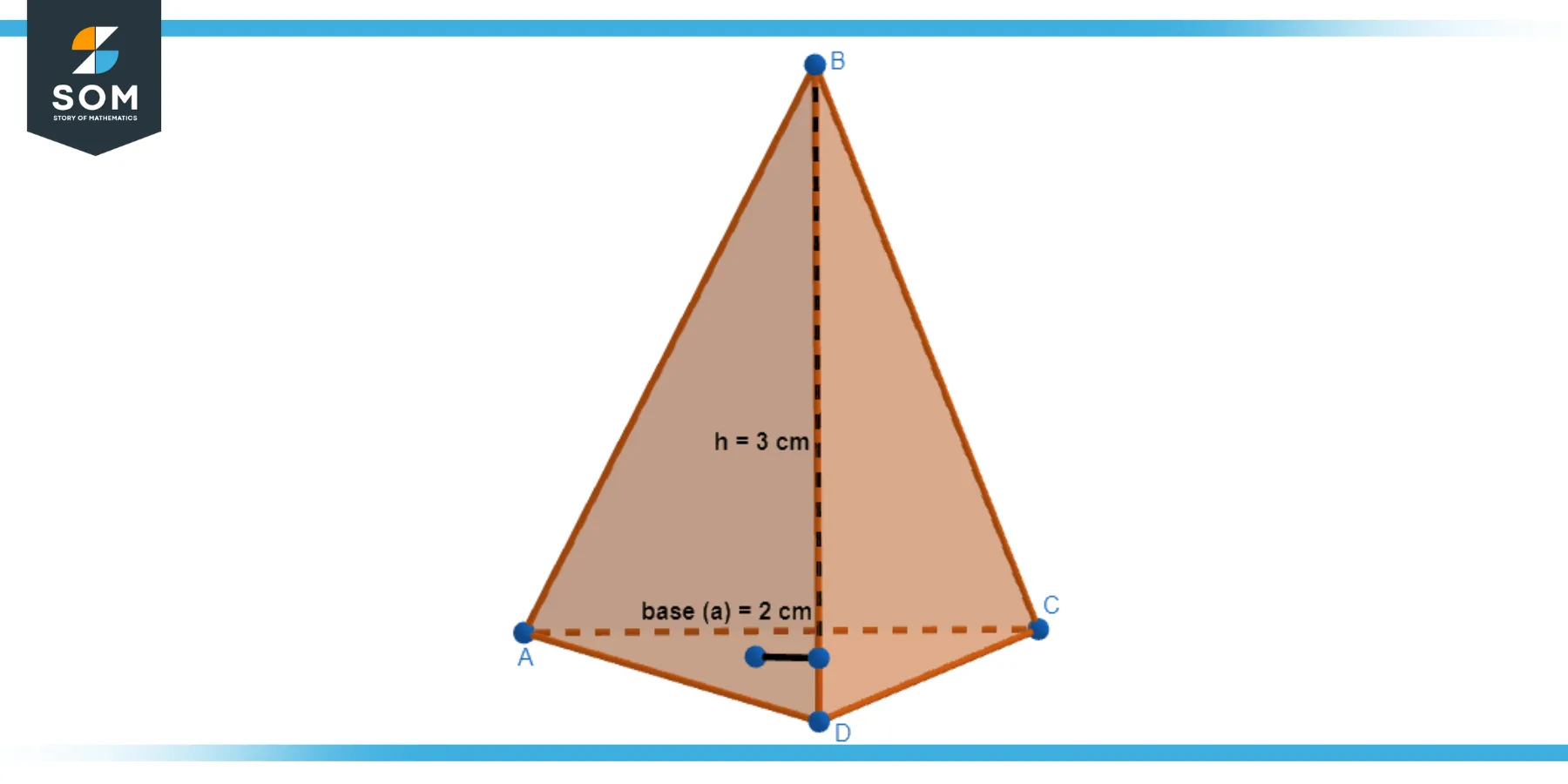
Solution
The base of the triangular pyramid: a = 2. Height of the triangular pyramid: h = 3.
The formula determines a triangular pyramid’s volume: V = (1/3) × base area × height.
Because the pyramid’s base is an equilateral triangle, its area can be determined using the following formula:
A = (√3/4) × a²
Substituting the values into the volume formula, we get:
V = (1/3) × (√3/4) × 2² × 3
V = 12 × (√3/12)
V = (√3)
Therefore, the volume of the triangular pyramid is (√3).
Example 2
Finding the Surface Area of a Triangular Pyramid Given
The base of the triangular pyramid: a = 2. Height of the triangular pyramid: h =3.
Solution
The surface area of a triangular pyramid can be calculated by finding the sum of the areas of its four faces.
Since the base of the pyramid is an equilateral triangle, each face is an equilateral triangle with side length a.
The area of an equilateral triangle is given by the formula:
A = (√3/4) × 2²
Thus, the total surface area of the triangular pyramid is 4 times the area of one face:
SA = 4 × (√3/4) × 2²
SA = √3 c 4
Therefore, the surface area of the triangular pyramid is √3 × 4.
Example 3
Finding the Height of a Triangular Pyramid Given
The base of the triangular pyramid: a = 3. The volume of the triangular pyramid: V = 2.
Solution
Using the formula for the volume of a triangular pyramid, we can rearrange it to solve for the height h.
V = (1/3) × (√3/4) × 3² × h
To find the height, we isolate h in the equation:
h = (3 × 2) / ((√3/4) × 9)
h = (4 × 2) / (√3 × 9)
h = (8) / (9√3)
h = (8) / (9√3)
h = (8√3) / 27
Therefore, the height of the triangular pyramid is (8√3) / 27.
Example 4
Finding the Slant Height of a Triangular Pyramid Given
The base of the triangular pyramid: a = 4. Height of the triangular pyramid: h= 3.
Solution
To find the slant height of a triangular pyramid, we need to calculate the length of the line segment connecting the apex to the center of the base.
The slant height can be determined using the Pythagorean theorem with the height h and half the side length a/2 as the two sides of a right triangle.
The slant height, denoted as s, can be found as follows:
s = √((4/2)² + 3²)
s = √((4/2)² + 9)
s = √(4 + 9)
s = √(13)
Therefore, the slant height of the triangular pyramid is √13.
Example 5
Finding the Circumradius of a Triangular Pyramid Given
The base of the triangular pyramid: a = 5.
Solution
The circumradius of a triangular pyramid can be determined by finding the radius of the sphere that circumscribes the pyramid.
For an equilateral triangle, the circumradius (denoted as R) is related to the side length a by the formula:
R = (5 / (2√3))
R = (5√3) / (2√3 × √3)
R = 1.44338.
Therefore, the circumradius of the triangular pyramid is 1.44338.
Example 6
Finding the Inradius of a Triangular Pyramid Given
The base of the triangular pyramid: a = 3.
Solution
The inradius of a triangular pyramid is the radius of the largest sphere that can fit inside the pyramid tangent to all four faces.
For an equilateral triangle, the inradius (denoted as r) is related to the side length a by the formula:
r = (3 / (2√6))
r =0.61237
Therefore, the inradius of the triangular pyramid is 0.61237.
Example 7
Finding the Diagonal Length of a Triangular Pyramid Given
The base of the triangular pyramid: a = 4. Height of the triangular pyramid: h = 5.
Solution
To find the diagonal length of a triangular pyramid, we need to calculate the length of a line segment connecting two opposite vertices of the base.
The diagonal length, denoted as d, can be determined using the Pythagorean theorem with the side length a, and the height has the two sides of a right triangle.
The diagonal length is given by:
d = √(4² + 5²)
d = √(16 + 25)
d = √(16 + 25)
d = √(41)
d = 6.40312
Therefore, the diagonal length of the triangular pyramid is 6.40312.
All images were created with GeoGebra.
