What is x^0 – Detailed Explanation & Examples

The answer to the question of what is x to the power of 0 is very simple and easy as $x^{0} = 1$.

It looks very simple, but the question of how x^{0} = 1 now arises, and how true it is for all the values of “$x$”.

What is $x^{0}$, when $x = 0$ itself?

In this complete guide, we will study the expression $x^{0}$ and what it means. Does the answer to $x^{0}$ always equal to “$1$” or are there some exceptions?

What Is x^0 Equal To?

X to the power of 0 is always equal to 1, which results in this formula: $x^{0} = 1$. This is an interesting question and there are various ways to answer this question. Let us discuss some of the answers that explain why $x^{0} = 1$.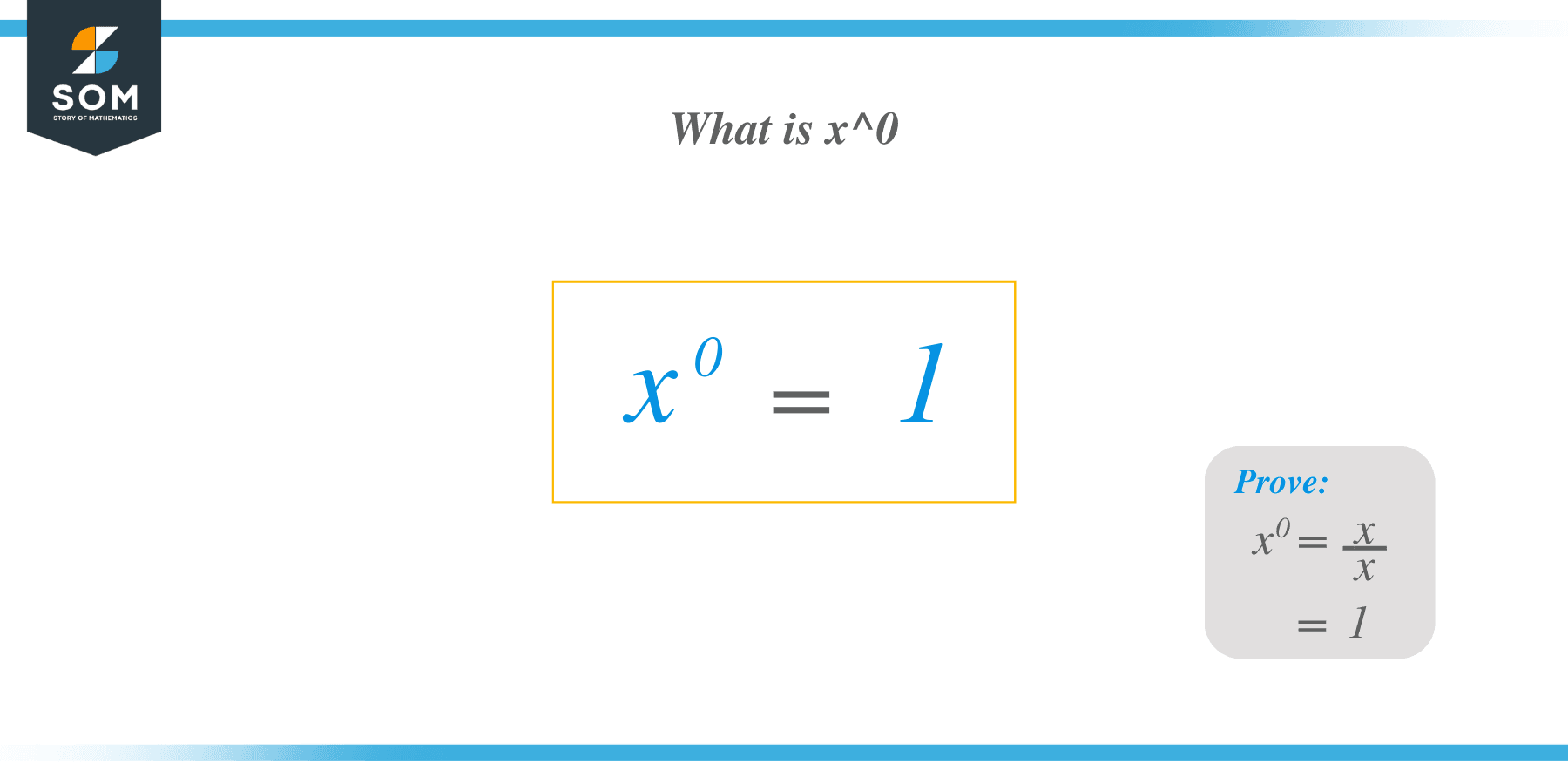

Answer 1

If any variable has power, we basically multiply the same variable by itself depending upon the power value on it. For example, $2^{2} = 2 \times 2 = 4$, $8^{4}= 8\times 8 \times 8 \times 8 = 4096$. So, if a variable has a power of “$0$”, then it means that we are multiplying the variable to itself zero times.

What does it mean that a variable is multiplying to itself zero times? Well, to explain this let us review the concepts of additive identity and multiplicative identity.

What is additive identity?

Additive identity states that when a number is added to “$0$”, the answer is the number itself. For example, when “$x$” is added to “$0$”, the answer is “$x$”: $x + 0 = x$. So basically, we can say that if we add no numbers to “$x$”, the answer will always be “$x$”. Adding no numbers is basically an additive identity.

Similarly, multiplying no numbers gives us a multiplicative identity that is equal to “$1$”. In the case of multiplicative identity, if we multiply any number by “$1$” it gives us the same number. For example, if a variable “$x$” is multiplied by “$1$”, the answer is “$x$”.

Our main question, “How is $x^{0} = 1$, $x^{0}$?” means that any number having zeroth power and any number to power zero means that no numbers are being multiplied with each other, and that is a multiplicative identity which is equal to “$1$”.

Hence, we can conclude that when no numbers are being multiplied, it gives us the multiplicative identity that is equal to “$1$”.

Answer 2

Any number or variable having a power means that we multiply that number or variable to that power. For example, if we are given $5^6$, we can write it as $5^{6}= 5\times 5\times \times 5 \times 5 \times 5 \times 5$. Now let us draw a pattern by decreasing the power by $”1”$.

$5^{6} = 5\times 5\times 5\times 5 \times 5 \times 5 \times 5 = 15,625$

$5^{5} = 5\times 5\times \times 5 \times 5 \times 5 = 3125$

$5^{4} = 5\times 5\times \times 5 \times 5 = 625$

$5^{3} = 5\times 5\times \times 5 = 125$

$5^{2} = 5\times 5 = 25$

$5^{1} = 5$

So if you look at the pattern closely, what is basically happening here? We are decreasing the power of “$5$” in each step and whenever we decrease one power, we divide the above expression by “$5$”. For example, $5^{6} = 15,625$, and if we divide it by “$5$” we will get $3125$, which is the next answer to $5^{5}$.

So what will happen when we divide $5^{1} = 5$ by “$5$”? The answer would be equal to “$1$”. Hence, any number to the power “$0$” will always be equal to “$1$”.

Answer 3

Any number to the power zero is always “$1$” and there is a quick method to prove it. For example, let us look at the sequence from $4^{1}$ to $4^{4}$.

$4^{1} = 4$

$4^{2} = 4\times 4\times = 16$

$4^{3} = 4\times 4\times 4 = 64$

$4^{4} = 4\times 4\times 4\times 4 = 216$

From the above sequences and patterns, we can deduce that:

$4^{3} = \dfrac{4^{4}}{4}$

$4^{2} = \dfrac{4^{3}}{4}$

$4^{1} = \dfrac{4^{2}}{4}$

x^0 = 1 proof

So we can form the formula for the power for any variable “$x$”

$x^{n-1}= \dfrac{x^n}{x}$.

$x^{0}$ will happen when the value of “$n$” is equal to “$1$”. Plugging in the value of “$n$” in above equation:

$x^{1-1} = \dfrac{x^1}{x}$

$x^{0} = \dfrac{x}{x} =1 = 1$

Hence, $x^{0} = 1$

Answer 4

Let us prove that any number to the power zero is always “$1$” by using the exponential rule of mathematics. When two numbers having the same base are multiplied by each other, we add their powers or exponents.

$x^{m}\times x^{n} = x^{m + n}$

When two numbers are having the same base and are divided by each other, their powers are subtracted from one another.

$\dfrac{x^{m}}{x^{n}} = x^{m – n}$

Now let us assume that the powers and bases are both the same. Consider two numbers, $x^{m}$ and $x^{n}$ while $m = n$, if both these numbers are divided with each other we will get

$\dfrac{x^{n}}{x^{n}} = x^{n – n} =x^{0}$

We know from the properties of rational and integer exponents that $x^{-n}= \dfrac{1}{x^{n}}$. So, any number having a negative exponent is basically denominator of number “$1$”.

With this, we can write:

$\dfrac{x^{n}}{x^{n}} = x^{n}. x^{-n} = x^{n}. \dfrac{1}{x^{n}}$

$\dfrac{x^{n}}{x^{n}} = x^{0} = 1$.

So if any number is divided by itself, the answer will always be zero and any number with the power zero is basically divided by itself. For example, $5^{0}$ can be written as $\dfrac{5}{5}$, $\dfrac{5^{2}}{5^{2}}$etc. Hence, any number with a zero exponent will always be zero.

Now that you have studied detailed reasoning why $x^{0}$ is always equal to “$1$”, you would be able to explain it to someone else, but what if someone asks you what is $0^{0}$ equal to? That means “What is $x^{0}$ when $x = 0$?” and the answer to this question is presented below.

What Is 0^0 Equal To?

This is a tricky question and to date, there are differences of opinions on this matter, as some mathematicians say that $0^{0} = 1$, while others say that it cannot be determined or it is an indeterminate form. What does $x^0 = 1$ actually mean and what happens if $x = 0$ when $x = 0$? We get $0^0$, so is $0^0 = 1$? We will discuss the justifications for both cases here.

Why 0^0 Is Equal To 1

Most of the mathematicians in the 1800s and initial 1900”s believed that $0^{0} = 1$ and there was a general consensus that $0^{0} = 1$. This holds for all basic algebra and polynomial series.

We know that a polynomial expression is written in the form $a_ox^{0} + a_1x^{1}……+ a_nx^{n}$ here “$x$” is the variable while “$a$” is the co-efficient. Polynomial addition is done termwise while their multiplication is done through multiplication property of distribution and exponents.

We can say that “$x$” in the polynomial expression are the indeterminates while “$a$” values are the coefficient and together they form a polynomial ring. A polynomial ring is a set of indeterminates with coefficients and it is represented as R[x].

In a polynomial ring $x^{0}$ is treated as the multiplicative identity of the polynomial expression (it is same point we discussed in answer 1). Thus, $x^{0}$ if multiplied by any polynomial function p(x) will always give us the result p(x). Let us look at an example of a binomial theorem $(1+ x)^{i} = \sum_{n=0}^{i}\binom{i}{n} x^{n}$ is only validated for $x = 0$ when the condition $0^{0} = 1$ exists.

Similarly, different power series identities like $\dfrac{1}{1 – x} = \sum_{k=0}^{\infty}x^{k}$ are only valid when $0^{0} = 1$. Likewise, in differentiation $\dfrac{d}{dx}x^{k}= kx^{k – 1}$ is also only valid for $k = 1$ when $x = 0$ only and only if $0^{0} = 1$.

Why 0^0 is Indeterminate or Undefined

We have made the case for $0^0 = 1$ and it is mostly used in algebra and basic mathematics. We have discussed why $x^{0}$ through examples of exponentials.

$5^{3} = 5\times 5\times \times 5 = 125$

$5^{2} = 5\times 5 = 25$

$5^{1} = 5$

$5^{0}= 1$

We know that each time we decrease the value of power, we are basically dividing the term with “$5$”. Let us take the case of negative powers of $5$.

$5^{-1} = \dfrac{1}{5}$

$5^{-2} = \dfrac{1}{25}$

Keeping in the view of the above example even when we have a negative base e.g. -5, its power to zero will always be 1 and when you plot the graph for $y = x^{0}$, you will see that when $x = 0$, the value of $y = 1$.

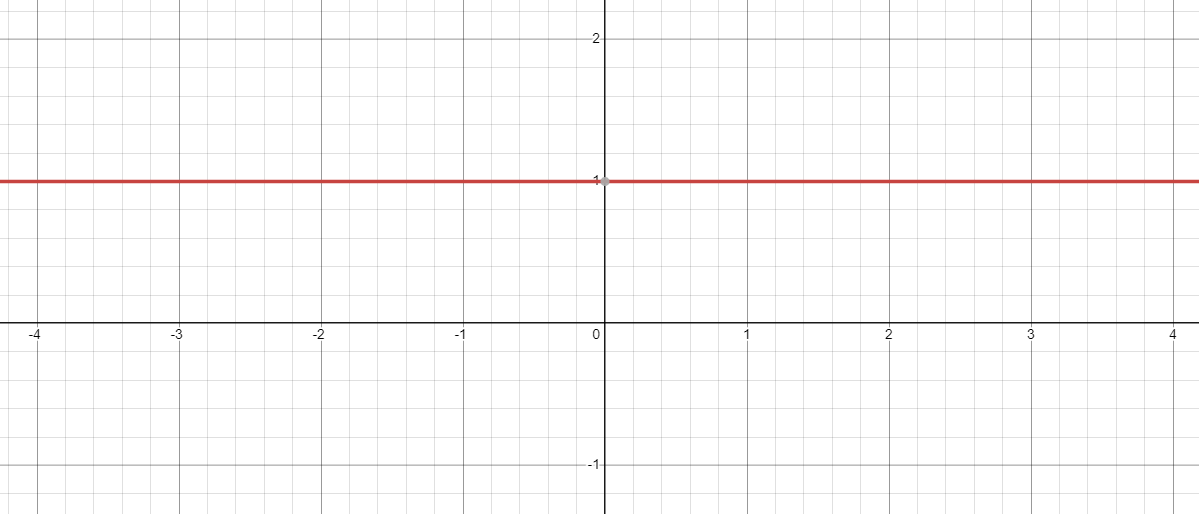
On the contrary, what happens if we take the equation $y = 0^{x}$? Here the base is constant while we are changing the exponent, so let us see if we decrease the value of “$x$” from $3$ to $1$.

$y = 0^{3} = 0$

$y = 0^{2}= 0$

$y = 0^{1}= 0$

Let us assume that $0^{0}= 1$, then

$0^{-1}$ should be $= \dfrac{0}{0}$ as $5^{-1}$ was $\dfrac{1}{5}$.

We know that anything divided by zero is infinity. So for $0^{x}$, what does $x=0$ on a graph look like? For expression $0^{x}$, what is $x=0$ called?

Well, the answer is simple as the answer is undefined in this case because $0^{x}$ is “1” for all positive values and infinity for all the negative values of “$x$”.

So is $x=0$ no solution in this case? The answer is yes and the graph will look like this:

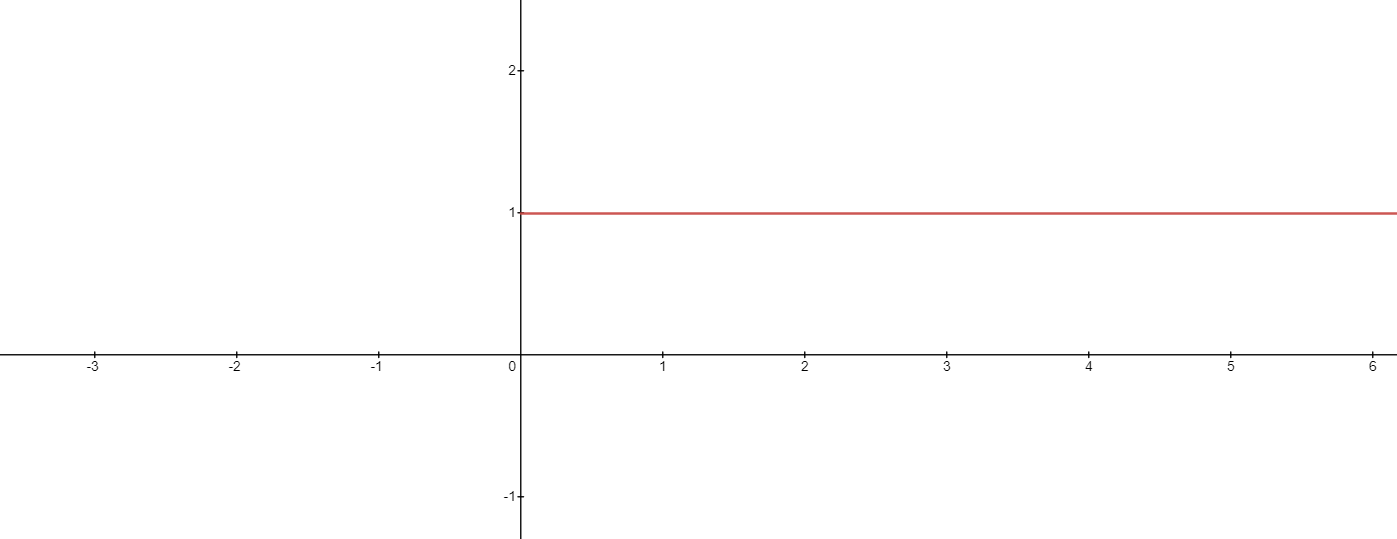
From the graph, we can draw the contradiction to $0^{0}$ being equal to $1$. So we can draw an interesting conclusion here, when we are dealing with the formula $x^{0}$ then $0^{0}$ will always be $1$.

But on the other hand, when are dealing with the formula $0^{x} then 0^{0}$ is undefined. This in itself creates ambiguity and this point has been raised by many mathematicians.

$0^{0}$ is also taken as an undefined term when you are studying calculus, specifically when you are studying the topics of limits, you will find out that $0^0$ is undefined or indeterminate.

When you are solving the problem of the limits and you are asked to evaluate the limit of $0^{0}$, then the limit of such form is always called the limits of indeterminate. We use special techniques like L’Hopital’s rule to solve such limits evaluating a limit of form $0^0$, and limits of that form are called “indeterminate forms.” You will need to use a special technique such as L’Hopital’s rule to evaluate them.

Let us take a simple limit $\lim_{x\to 0^{+}}f(x)$, what would happen if the function is of the form $[f(x)]^{g(x)}$, while $f(x) = 0$, $g(x) = 0$ and $x$ is approaching to 0 this gives us an indeterminant answer.

If we are given a two variable function, say $t^{n}$, and it is continuous on ${(t,n): t > 0}$ but it will not be continuous on ${(t,n): t > 0} U {(0,0)}$ no matter what is the value of $0^{0}$. Hence, while solving the limits and calculus problems it is desired that $0^{0}$ is taken as undefined term.

So, $x^{0} = 1$ is the general consensus while questions are made whether or not $0^0 =1$ or not. You now have an in-depth idea about the topic, but if you really want to dig deep into the debate of whether or not $0^0 = 1$, you can study the work of the mathematicians listed below.

1.  George Baron
2.  Augustin-Louis Cauchy
3.  Leonhard Euler

The Difference Between $(-1)^{0}$ And $-1^{0}$

Yes, there is a difference in $(-1)^{0}$ and $-1^{0}$. In the expression $(-1)^{0}$, we are taking “$0$” as the power for number “$-1$” so in short, the base is “$-1$” and answer for $(-1)^{0} = 1$. While for $-1^{0}$, the base is “$1$” as $-1$ is basically “$-1 \times 1$”, $1^{0 }= 1$ while the negative signs make it “$-1$”. Hence, $-1^{0} = -1$.

Is There Any Difference Between Exponent and Power?

Yes, there is a major difference between exponent and power, as Power is considered as a whole expression or answer. Any base to an exponent or its answer is considered power. For example, 81 is considered as the power of 3, since $3^{4} = 81$. In this example, “$3$” is the base while “$4$” is the exponent, and the expression $3^{4}$ is considered as power.

Conclusion

Let us summarize the whole article through the list of points below.

• In simple mathematics and generally speaking, x^0 will always be equal to 1.
•  x^0 = 1, and x = 0 when we are dealing with simple algebra, polynomials, and power series, while 0^0 is undefined in several topics of calculus, most prominently when dealing with limits or L’hopital’s rule.
• When the base is not zero, for example, when we are given x^0, then it will always be equal to 1. But when we are given zero as a base and the exponent is variable 0^x, then 0^0 will be undefined as “0” to power negative values, giving us undefined values or infinity as an answer.