- Home
- >
- Area of Triangle – Explanation & Examples
Area of Triangle – Explanation & Examples
 In this article, you will learn the area of a triangle and determine the area of different types of triangles. The area of a triangle is the amount of space inside the triangle. It is measured in square units.
In this article, you will learn the area of a triangle and determine the area of different types of triangles. The area of a triangle is the amount of space inside the triangle. It is measured in square units.
Before getting into the topic of a triangle area, let’s familiarize ourselves with terms such as the base and height of a triangle.
The base is the side of a triangle which is considered to be the bottom, while the height of a triangle is the perpendicular line dropped onto its base from the vertex opposite to the base.
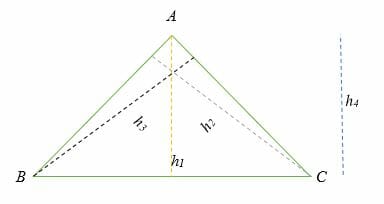
In the illustration above, the dotted lines are the possible heights of △ABC. Note that every triangle has, possibly, three heights or altitudes.
- The height of triangle △ABC is equal to h1 when the base is a side.
- The height of triangle △ABC is equal to h2 when the base is AB.
- The height of triangle △ABC is equal to h3 when the base is
- The height of triangle △ABC can be outside a triangle (h4), which is the same as the height h1.
From the illustrations above, we can make the following observations:
- The height of a triangle depends on its base.
- The perpendicular to the base of a triangle is equal to the height of the triangle.
- The height of a triangle can be outside the triangle.
Having discussed the concept of the height and the base of a triangle, let’s now embark on how to calculate the area of a triangle.
How to Find the Area of a Triangle?
The area of a rectangle is well known to us, i.e., length * width. What will happen if we bisect the rectangle diagonally (cut into half)? What will be its news area? For example, in a rectangle with a base and height of 6 units and 12 units, respectively, the rectangle area is 72 square units.
Now, if you divide it into two equal halves (after bisecting the rectangle diagonally), the area of two new shapes must be 36 square units each. The two news shapes are triangles. That means if the rectangle is diagonally cut into two equal halves, the two new shapes formed are triangles, where each triangle has an area equal to ½ of the area of the rectangle.
The area of a triangle is the total space or region enclosed by a particular triangle.
The area of a triangle is the product of the base and height divided by 2.
The standard unit for measurement of the area is square meters (m2).
Other units include:
- Square millimeters (mm2)
- Square inches (in2)
- Square kilometers (km2)
- Square yards.
Area of a Triangle Formula
The general formula for calculating the area of a triangle is;
Area (A) = ½ (b × h) square units, where; A is the area, b is the base, and h is the triangle’s height. The triangles might be different in nature, but it important to note that this formula applies to all the triangles. Different types of triangles have different area formulas.
Note: The base and height must be in the same units, i.e., meters, kilometers, centimeters, etc.
Area of a right triangle
The area of a triangle = (½ × Base × Height) square units.
Example 1
Find the area of the right-angled triangle whose base is 9 m and height is 12m.
Solution
A = ¹/₂ × base × height
= ¹/₂ × 12 × 9
= 54 cm²
Example 2
The base and height of a right triangle are 70 cm and 8 m, respectively. What is the area of the triangle?
Solution
A = ½ × base × height
Here, we have 70 cm and 8 m. You can choose to work with cm or m. Let’s work in meters by changing 70cm to meters.
Divide 70cm by 100.
70/100 = 0.7m.
⇒ A = (½ × 0.7 × 8) m2
⇒ A = (½ x 5.6) m2
⇒ A = 2.8m2
Area of an isosceles triangle
An isosceles triangle is a triangle whose two sides are equal and also two angles are equal. The formula for the area of an isosceles triangle is;
⇒A = ½ (base × height).
When the height of an isosceles triangle is not given, then the following formula is used to find the height:
Height= √ (a2 − b2/4)
Where;
b = base of the triangle
a = Side length of the two equal sides.
Therefore, the area of an isosceles triangle can be;
⇒A = ½ [√ (a2 − b2 /4) × b]
Also, the area of an isosceles right triangle is given by:
A= ½ × a2, where a = Side length of the two equal sides
Example 3
Calculate the area of an isosceles triangle whose base is 12 mm and height is 17 mm.
Solution
⇒A = ½ × base × height
⇒ 1/2 × 12 × 17
⇒ 1/2 × 204
= 102 mm2
Example 4
Find the area of an isosceles triangle whose side lengths are 5m and 9m
Solution
Let the base, b = 9 m and a = 5m.
⇒ A = ½ [√ (a2 − b2 /4) × b]
⇒ ½ [√ (52 − 92 /4) × 9]
= 9.81m2
Area of an equilateral triangle
An equilateral triangle is a triangle in which the three sides are equal and the three interior angles equal. The area of an equilateral triangle is:
A = (a2√3)/4
Where a = length of the sides.
Example 5
Calculate the area of an equilateral triangle whose side is 4 cm.
Solution
⇒ A = (a2 /4) √3
⇒ (42/4) √3
⇒ (16/4) √3
= 4√3 cm2
Example 6
Find the area of an equilateral triangle whose perimeter is 84 mm.
Solution
The perimeter of an equilateral triangle = 3a.
⇒ 3a = 84 mm
⇒ a = 84/3
⇒ a = 28 mm
Area = (a2 /4) √3
⇒ (282/4) √3
= 196√3 mm2
Area of a scalene triangle
A scalene triangle is a triangle with 3 different side lengths and 3 different angles. The area of a scalene triangle can be calculated using Heron’s formula.
Heron’s formula is given by;
⇒ Area = √ {p (p – a) (p – b) (p – c)}
where ‘p’ is the semi-perimeter and a, b, c are the side lengths.
⇒ p = (a + b + c) / 2
Example 7
Calculate the area of a triangle whose side lengths are 18mm, 20mm, and 12mm.
Solution
⇒ p = (a + b + c) / 2
Substitute the values of a, b and c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Area = √ {p (p – a) (p – b) (p – c)}
= √ {25 x (25 – 12) x (25 – 18) x (25 – 20)}
= √ (25 x 13 x 7 x 5)
= 5√455 mm2
