JUMP TO TOPIC

This article aims to shed light on the arcsec derivative, exploring its fundamental properties, applications, and the inherent elegance it brings to mathematical analysis. So, let us embark on this mathematical journey and delve into the depths of the arcsec derivative to uncover its hidden treasures.
Defining arcsec Derivative
The arcsec derivative represents the rate of change of the arcsecant function with respect to its input variable.
More formally, if we consider a function f(x) = arcsec(x), where arcsec(x) is the inverse of the secant function, then the derivative of f(x) with respect to x is known as the arcsec derivative. It quantifies how the output of the arcsecant function changes as its input variable x varies.
The arcsec derivative is a crucial mathematical tool for analyzing and solving problems involving inverse trigonometric functions, and it allows us to explore the behavior and properties of the arcsecant function in various contexts, such as calculus, physics, and engineering.
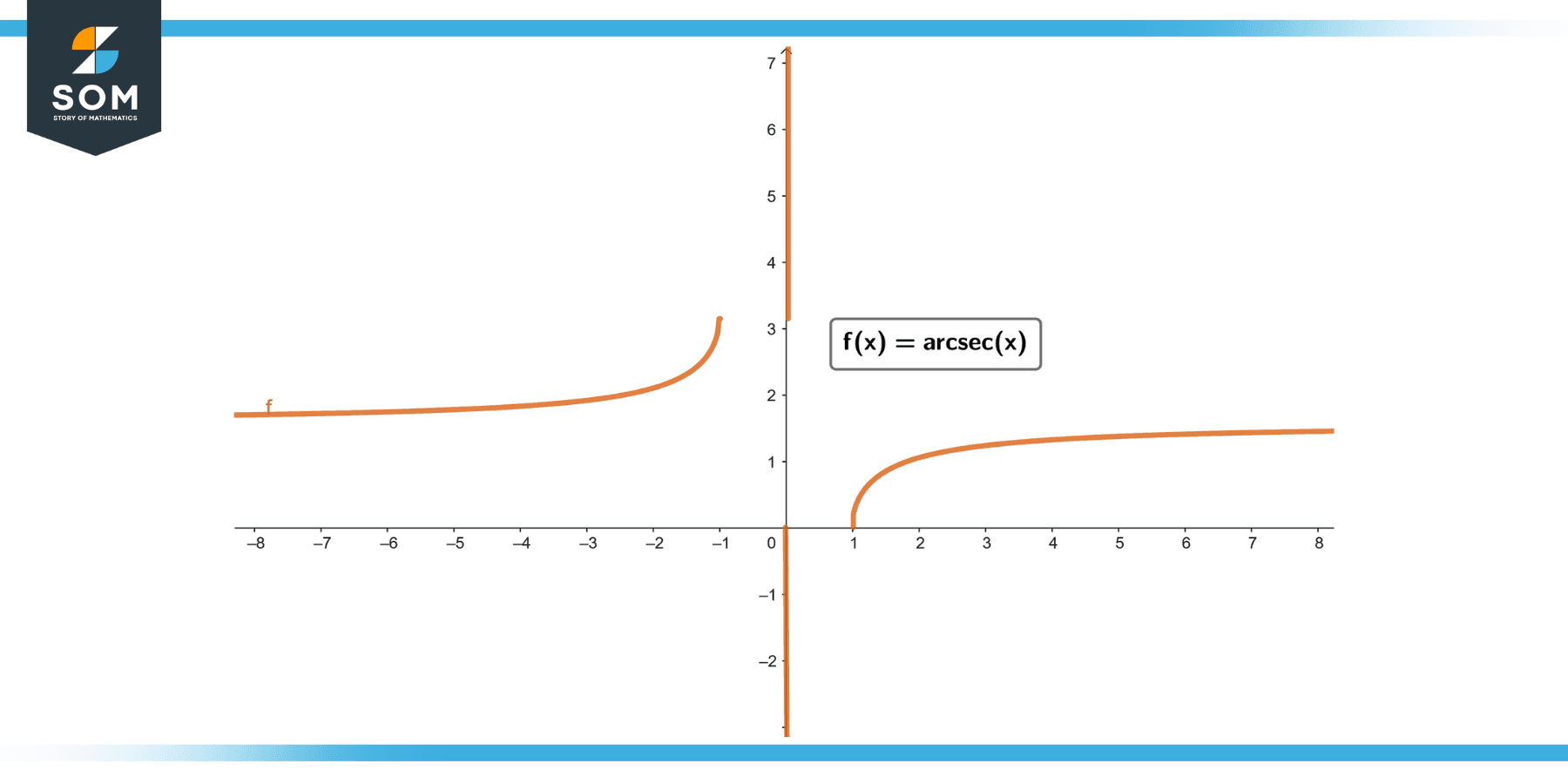
Figure-1.
Properties of arcsec Derivative
Here are the properties of the arcsec derivative explained in detail:
Domain and Range
The arcsec derivative is defined for a specific domain. The function arcsec(x) itself is defined for x ∈ (-∞, -1] ∪ [1, +∞), excluding the values where x = 0. Consequently, the arcsec derivative is defined for the same domain as the arcsecant function.
Differentiability
The arcsec derivative is differentiable for its domain. However, it is important to note that the arcsecant function itself is not differentiable at the points where its value equals ±∞. This means that the arcsec derivative will also be non-differentiable at those particular points.
Formula
The arcsec derivative can be expressed using calculus notation as d/dx (arcsec(x)). To find the derivative, we use the inverse trigonometric identity d/dx (arcsec(x)) = 1 / (|x|√(x^2 – 1)). It is worth noting that this formula holds true for x ∈ (-∞, -1) and x ∈ (1, +∞).
Positive and Negative Values
The arcsec derivative can be positive or negative depending on the value of x. When x > 1, the derivative is positive, indicating an increasing slope. Conversely, when x < -1, the derivative is negative, representing a decreasing slope. These signs are a consequence of the square root term in the derivative formula.
Asymptotic Behavior
The arcsec derivative approaches zero as x approaches ±∞. This implies that the rate of change of the arcsecant function becomes smaller and smaller as the input variable moves towards infinity or negative infinity.
Critical Points
The arcsec derivative has critical points at x = ±1. At these points, the derivative is undefined (since the denominator of the derivative formula becomes zero), which corresponds to the vertical asymptotes of the arcsecant function.
Applications
The arcsec derivative finds application in various mathematical and scientific fields. It is utilized in calculus to solve problems involving rates of change, optimization, and integration. In physics and engineering, the arcsec derivative helps analyze systems with angular measurements and plays a role in fields like optics, mechanics, and control systems.
Understanding the properties of the arcsec derivative allows us to comprehend the behavior of the arcsecant function and apply it to solve problems across different disciplines. By leveraging these properties, mathematicians, scientists, and engineers can delve deeper into the intricacies of inverse trigonometric functions and their applications.
Ralevent Formulas
Here are the related formulas for the arcsec derivative explained in detail:
Using the Inverse Trigonometric Identity
The arcsec derivative can be derived using the inverse trigonometric identity that relates the derivative of an inverse trigonometric function to the function itself. Specifically, for the arcsecant function, the identity is:
d/dx (arcsec(x)) = 1 / (|x|√(x² – 1))
Here, d/dx denotes the derivative with respect to x. The formula holds true for x ∈ (-∞, -1) and x ∈ (1, +∞), excluding the values where x = 0.
Simplifying the Formula
To simplify the formula further, we can manipulate it by using algebraic techniques. The derivative formula can be rewritten as:
d/dx (arcsec(x)) = ±1 / (|x|√(x² – 1))
Note that the positive or negative sign depends on the interval of x. For x > 1, the positive sign is taken, while for x < -1, the negative sign is used. This is because the arcsecant function is positive in the interval (1, +∞) and negative in the interval (-∞, -1).
Derivative at x = 1 and x = -1
At the critical points x = 1 and x = -1, the derivative formula becomes undefined, as the denominator becomes zero. This aligns with the vertical asymptotes of the arcsecant function.
Simplifying Further
The derivative formula can be further simplified by factoring out |x| from the denominator, resulting in:
d/dx (arcsec(x)) = ±1 / (|x|√(x² – 1))
d/dx (arcsec(x)) = ±1 / (|x| ∙ |√(x² – 1)|)
d/dx (arcsec(x)) = ±1 / (|x| ∙ √|x² – 1|)
This form highlights the relationship between the arcsec derivative and the absolute value of x, as well as the absolute value of the square root of (x² – 1).
Alternative NotationsIn some mathematical contexts, different notations may be used to represent the arcsec derivative. Some common alternative notations include $d/dx (sec^(-1)(x))$ and d/dx (asec(x)).
Understanding and utilizing these formulas for the arcsec derivative allows for the analysis of the rate of change and behavior of the arcsecant function in various mathematical and scientific applications. These formulas provide valuable tools for solving problems involving inverse trigonometric functions, optimization, integration, and other areas of mathematics and physics.
Exercise
Example 1
Find the derivative of 𝑓(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(2𝑥).
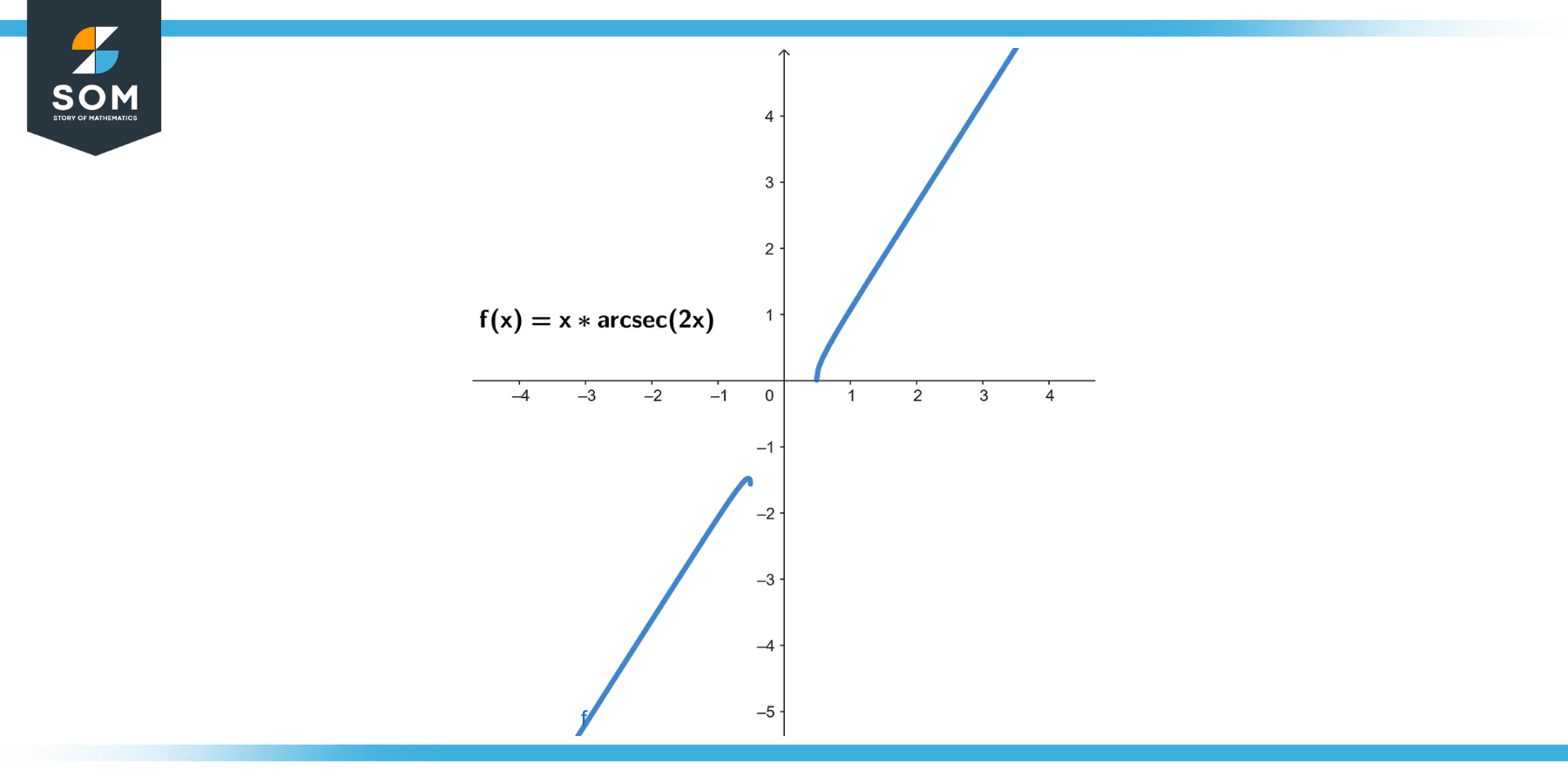
Figure-2.
Solution
To find the derivative of 𝑓(𝑥), we apply the chain rule. Let 𝑢 = 2𝑥. Then, 𝑓(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑢). Using the derivative formula, we have:
𝑓'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑢))
𝑓'(𝑥) = 1 / (|𝑢|√(𝑢² – 1))
Substituting back 𝑢 = 2𝑥:
𝑓'(𝑥) = 1 / (|2𝑥|√((2𝑥)² – 1))
𝑓'(𝑥) = 1 / (|2𝑥|√(4𝑥² – 1))
Thus, the derivative of 𝑓(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(2𝑥) is 𝑓'(𝑥) = 1 / (|2𝑥|√(4𝑥² – 1)).
Example 2
Find the derivative of 𝑔(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(5𝑥 + 3).
Solution
Similar to the previous example, we apply the chain rule. Let 𝑢 = 5𝑥 + 3. Then, 𝑔(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑢). Using the derivative formula, we have:
𝑔'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑢))
𝑔'(𝑥) = 1 / (|𝑢|√(𝑢² – 1))
Substituting back 𝑢 = 5𝑥 + 3:
𝑔'(𝑥) = 1 / (|5𝑥 + 3|√((5𝑥 + 3)² – 1))
Therefore, the derivative of 𝑔(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(5𝑥 + 3) is 𝑔'(𝑥) = 1 / (|5𝑥 + 3|√((5𝑥 + 3)² – 1)).
Example 3
Find the derivative of ℎ(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥²).
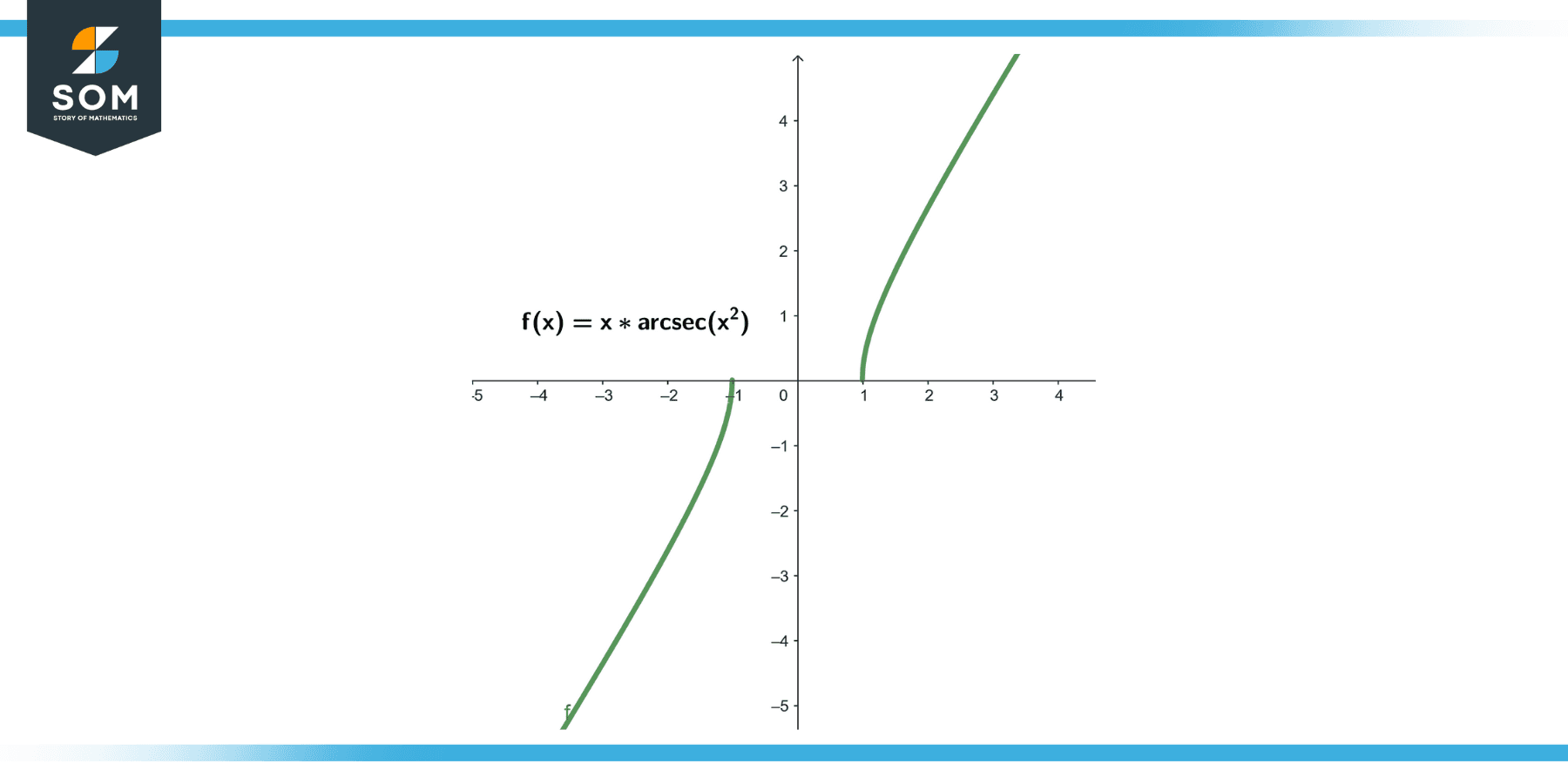
Figure-3.
Solution
To differentiate ℎ(𝑥), we again apply the chain rule. Let 𝑢 = 𝑥². Then, ℎ(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑢). Using the derivative formula, we have:
ℎ'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑢))
ℎ'(𝑥) = 1 / (|𝑢|√(𝑢² – 1))
Substituting back 𝑢 = 𝑥²:
ℎ'(𝑥) = 1 / (|𝑥²|√((𝑥²)² – 1))
ℎ'(𝑥) = 1 / (|𝑥²|√(𝑥⁴ – 1))
Thus, the derivative of ℎ(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥²) is ℎ'(𝑥) = 1 / (|𝑥²|√(𝑥⁴ – 1)).
Example 4
Find the derivative of 𝑘(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(3 / 𝑥).
Solution
Using the chain rule, we let 𝑢 = 3 / 𝑥. Then, 𝑘(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑢). Applying the derivative formula, we have:
𝑘'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑢))
𝑘'(𝑥) = 1 / (|𝑢|√(𝑢² – 1))
Substituting back 𝑢 = 3 / 𝑥:
𝑘'(𝑥) = 1 / (|3 / 𝑥|√((3 / 𝑥)² – 1))
𝑘'(𝑥) = 1 / (|3 / 𝑥|√((9 / 𝑥²) – 1))
𝑘'(𝑥) = 𝑥 / (3√(9 – 𝑥²))
Therefore, the derivative of 𝑘(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(3 / 𝑥) is 𝑘'(𝑥) = 𝑥 / (3√(9 – 𝑥²)).
Example 5
Find the derivative of 𝑚(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(√𝑥).
Solution
To differentiate 𝑚(𝑥), we use the chain rule. Let 𝑢 = √𝑥. Then, 𝑚(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑢). Applying the derivative formula, we have:
𝑚'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑢))
𝑚'(𝑥) = 1 / (|𝑢|√(𝑢² – 1))
Substituting back 𝑢 = √𝑥:
𝑚'(𝑥) = 1 / (|√𝑥|√((√𝑥)² – 1))
𝑚'(𝑥) = 1 / (|√𝑥|√(𝑥 – 1))
Hence, the derivative of 𝑚(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(√𝑥) is 𝑚'(𝑥) = 1 / (|√𝑥|√(𝑥 – 1)).
Example 6
Find the derivative of 𝑛(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(2𝑥 – 1) + 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥²).
Solution
To find the derivative of 𝑛(𝑥), we differentiate each term separately and sum the results.
For the first term, let 𝑢 = 2𝑥 – 1. Then, 𝑛(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑢). Applying the derivative formula, we have:
𝑛'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑢))
𝑚'(𝑥) = 1 / (|𝑢|√(𝑢² – 1))
Substituting back 𝑢 = 2𝑥 – 1:
𝑛'(𝑥) = 1 / (|2𝑥 – 1|√((2𝑥 – 1)² – 1))
For the second term, let 𝑣 = 𝑥². Then, 𝑛(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑣). Using the derivative formula, we have:
𝑛'(𝑥) = d/d𝑥 (𝑎𝑟𝑐𝑠𝑒𝑐(𝑣))
𝑛'(𝑥) = 1 / (|𝑣|√(𝑣² – 1))
Substituting back 𝑣 = 𝑥²:
𝑛'(𝑥) = 1 / (|𝑥²|√((𝑥²)² – 1))
𝑛'(𝑥) = 1 / (|𝑥²|√(𝑥⁴ – 1))
Therefore, the derivative of 𝑛(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(2𝑥 – 1) + 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥²) is 𝑛'(𝑥) = 1 / (|2𝑥 – 1|√((2𝑥 – 1)² – 1)) + 1 / (|𝑥²|√(𝑥⁴ – 1)).
Example 7
Find the derivative of 𝑝(𝑥) = 𝑥 * 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥).
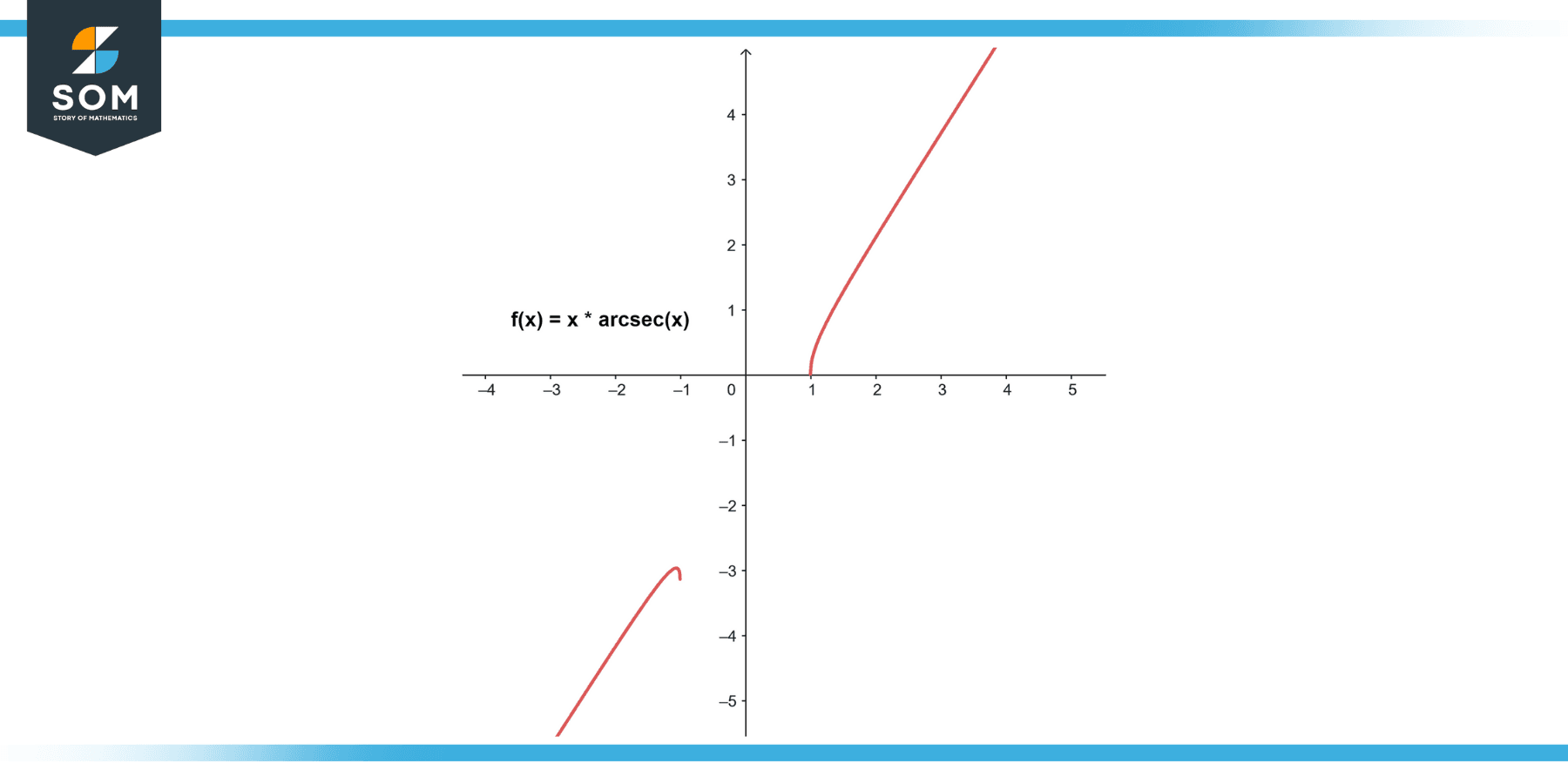
Figure-4.
Solution
To differentiate 𝑝(𝑥), we apply the product rule. Let 𝑓(𝑥) = 𝑥 and 𝑔(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥). Using the product rule, we have:
𝑝'(𝑥) = 𝑓'(𝑥) * 𝑔(𝑥) + 𝑓(𝑥) * 𝑔'(𝑥)
Differentiating 𝑓(𝑥) = 𝑥, we have 𝑓'(𝑥) = 1.
For 𝑔(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥), we apply the derivative formula:
𝑔'(𝑥) = 1 / (|𝑥|√(𝑥² – 1))
Combining these results, we have:
𝑝'(𝑥) = 1 * 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥) + 𝑥 * (1 / (|𝑥|√(𝑥² – 1)))
𝑝'(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥) + 1 / (√(𝑥² – 1))
Thus, the derivative of 𝑝(𝑥) = 𝑥 * 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥) is 𝑝'(𝑥) = 𝑎𝑟𝑐𝑠𝑒𝑐(𝑥) + 1 / (√(𝑥² – 1)).
Applications
The arcsec derivative, with its ability to analyze the rate of change of the arcsecant function, finds applications in various fields. Here are some examples of its applications in different areas:
Calculus
The arcsec derivative plays a significant role in calculus, particularly in problems involving rates of change. By understanding the behavior of the arcsecant function, one can determine the instantaneous rate of change at a specific point, enabling the solution of optimization problems and related calculus tasks.
Physics
In physics, angular measurements and trigonometric functions are commonly encountered. The arcsec derivative allows for the analysis of systems involving angles, such as rotational motion, oscillatory behavior, and wave propagation. By applying the arcsec derivative, physicists can determine how these systems change over time and quantify angular velocities and accelerations.
Engineering
Engineers often encounter inverse trigonometric functions in various disciplines, including control systems, robotics, signal processing, and optics. The arcsec derivative helps engineers analyze and design systems that involve angles, such as robotic arm movements, stabilization of control systems, and optical lens design.
Mathematics Education
The arcsec derivative is an important concept taught in mathematics education, specifically in calculus courses. It helps students understand the behavior of inverse trigonometric functions and their derivatives.
Scientific Research
The arcsec derivative is utilized in scientific research that involves the analysis and modeling of data containing angles or angular relationships. It enables researchers to quantify changes in angular quantities, validate experimental data, and derive mathematical models to describe and predict phenomena in various scientific disciplines.
Computer Graphics and Animation
In computer graphics and animation, angles and trigonometric functions are fundamental for creating realistic movements and visual effects. The arcsec derivative helps in determining the rate of change of angles, which influences the smoothness and realism of animations, simulations, and virtual environments.
By applying the arcsec derivative in fields such as computer graphics, animation, physics, engineering, and mathematics, mathematicians, scientists, engineers, and educators can analyze, optimize, and model systems involving angles and angular measurements.
It provides a valuable tool for understanding and quantifying the behavior of inverse trigonometric functions, contributing to advancements in various scientific, technological, and mathematical endeavors.
Historical Significance
The concept of the arcsec derivative and other inverse trigonometric functions emerged from the development of trigonometry and its applications in mathematics and science. Trigonometry itself has a long and rich history, with roots dating back to ancient civilizations.
The ancient Greeks, particularly Hipparchus (c. 190 – c. 120 BCE) and Ptolemy (c. 90 – c. 168 CE), made significant contributions to trigonometry by studying the relationships between angles and sides of triangles.
They developed tables of chord lengths, which were later transformed into tables of arc lengths. However, it wasn’t until the medieval Islamic mathematicians, such as Al-Battani (c. 858 – c. 929 CE) and Al-Kashi (c. 1380 – 1429 CE), that the inverse trigonometric functions began to take shape.
The term “arcsecant” itself comes from the Latin words “arcus secans,” which mean “the cutting arc.” It refers to the inverse of the secant function, which is the reciprocal of the cosine function. The development of inverse trigonometric functions, including the arcsecant, was necessary for solving equations involving angles in trigonometry and astronomy.
The formal study of derivatives and calculus emerged later in the 17th century with the contributions of mathematicians such as Isaac Newton and Gottfried Wilhelm Leibniz. Their work provided a systematic framework for understanding rates of change, tangents to curves, and the derivative as a mathematical concept.
As calculus and the study of derivatives progressed, the derivative of inverse trigonometric functions, including the arcsecant derivative, became part of the mathematical discourse. Mathematicians developed formulas and techniques to differentiate inverse trigonometric functions to solve various problems in calculus and related fields.
All images were created with GeoGebra.
