JUMP TO TOPIC
 The AC method is a mathematical method that is used in the factorization of quadratic functions.
The AC method is a mathematical method that is used in the factorization of quadratic functions.
The AC method is also called the lazy ac method, and it is used to determine whether the factors of the given function can be determined or not. It can also be used for factoring polynomials or, more specifically speaking, factoring quadratics equations.
We know that a quadratic equation is written as:
$Ax^{2} + Bx + C$
In this formula, A and B are the coefficients, so C is the constant. The name AC is given because this method utilizes the product of coefficient A and constant C to find out the factors of the quadratic function.
In this guide, we will discuss how the AC method can be used to determine the factors of a quadratic trinomial function by studying different numerical examples.
What Is Meant by AC Method?
The AC method is a faction method which is used to determine if the factorization of a quadratic trinomial is possible or not. It is used to determine the factors of a quadratic trinomial function.
For example, if we are given a quadratic trinomial $Ax^{2} + Bx + C$, then according to the AC method, the product of A and C will give us two factors, say P and Q, and when we add these two factors, then the addition will be equal to coefficient B. These factors are also called factor trinomials.
First of all, let us discuss what is meant by a quadratic trinomial and then we will apply the AC method to solve for the factors of the quadratic trinomial.
Quadratic Trinomial
When a polynomial function has a power/degree of two and it also consists of three terms, then it is said to be a quadratic trinomial. The general expression of a quadratic trinomial is written as $Ax^{2} + Bx + C$. For example, the quadratic function $3x^{2} + 5x + 6$ is a quadratic trinomial.
In the quadratic polynomial $3x^{2} + 5x + 6$, $A = 3$, $B = 5$ and $C = 6$ all of these are integers. A quadratic trinomial can take any of the forms given below:
- A quadratic terminal equation with the constant as a positive integer
- A quadratic terminal equation with constant as a negative integer
- A general quadratic terminal equation
- An equation containing only terminal squares.
A normal quadratic trinomial equation is written as $Ax^{2} + Bx + C$, while a trinomial square equation’s first term and last term are positive squares. For example, the trinomials $x^{2} + 2xy + y^{2}$ and $x^{2} – 2xy + y^{2}$ are square trinomials as the first and last terms are both positive squares while the middle term can be either positive or negative.
Factoring Quadratic Trinomials Using AC Method
Factoring trinomials or quadratic trinomials using the AC method is quite easy and simple. The steps below are to be followed while factoring a trinomial quadratic equation.
- Identify or verify a quadratic trinomial equation.
- Multiply A and C and find two factors, P and Q.
List all the factors of the product and check if the two factors summation is equal to B and their product should also be equal to the product of AC.
- If the third step is successful, then rewrite the equation with the newly found factors in the previous step.
- Separate the similar terms and then factor out the greatest common factor, and this will give us the factors of the given trinomial equation.
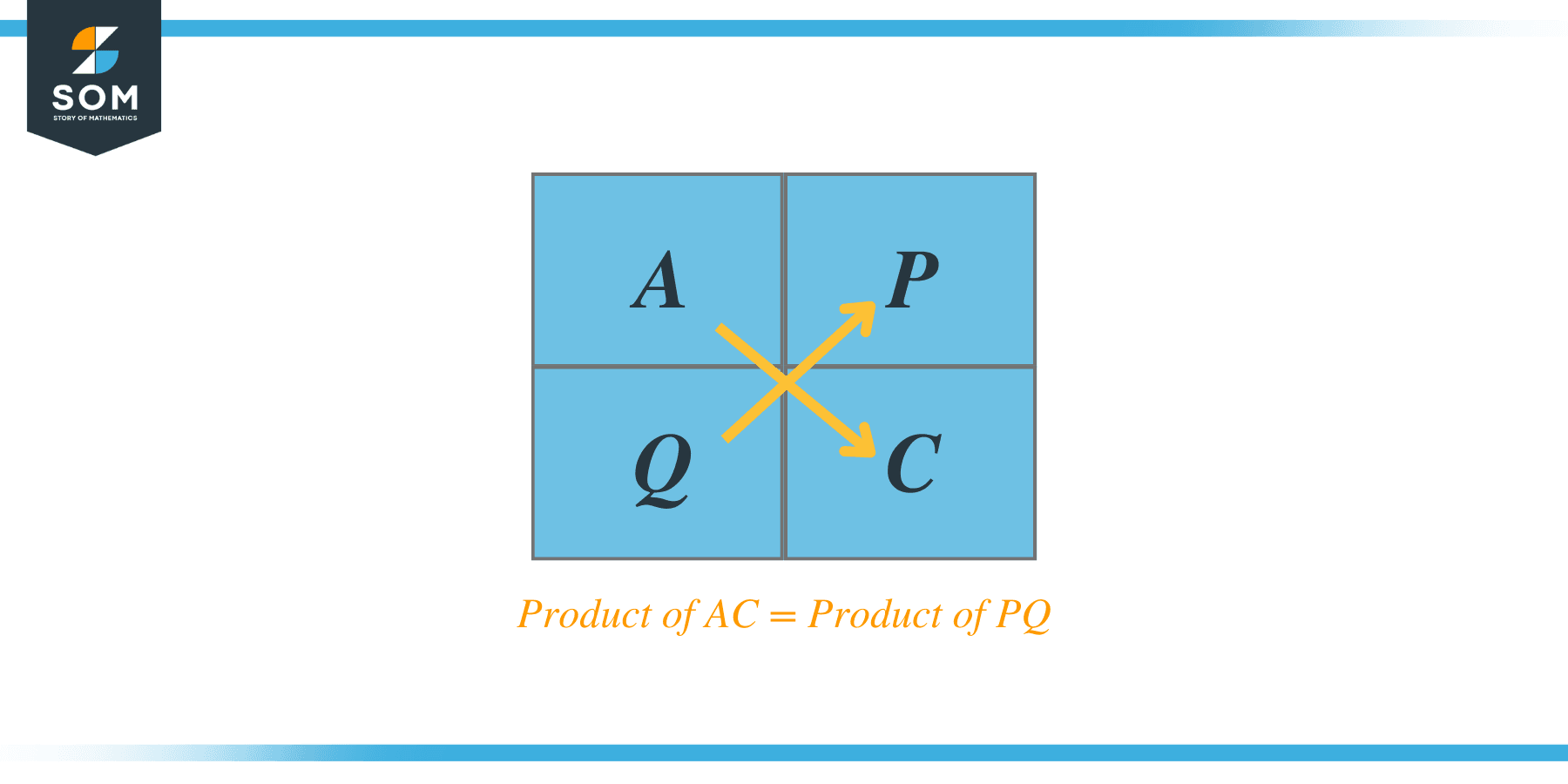
Let us take an example of trinomial quadratic equation $2x^{2} + 7x + 6$. Now let us solve it step by step using the AC method.
$2x^{2} + 7x + 6$
$A = 2$ and $C = 6$
$AC = 2 \times 6 = 12$ (Remember that the actual product is $12x^{2}$. In the AC method, we will be only multiplying the coefficients or constant values together.)
$B = 7$
The next step is to find the two factors which, when multiplied, give the answer as $12$. The factors can be:
$P = 12$, $Q = 1$, $12 = (12) (1)$
$P = 4 $, $Q = 3$, $12 = (4) (3)$
$P = 6 $, $Q = 2$, $12 = (6) (2)$
Now we will choose the two factors which, when added together, should be equal to $B = 7$. In this case, those factors are $P = 4$ and $Q = 3$. As $4 + 3 = 7 = B$.
As discussed earlier, we are only multiplying the coefficients $4x + 3x = 7x$ and the product of the factors P and Q $4x \times 3x = 12x^{2}$, which is equal to $AC = 2x^{2} \times 6 = 12x^{2}$
Now we will rewrite the equation as:
$2x^{2} + 4x + 3x + 6$
2x ( x +2) + 3 ( x +2)$
$(x+2) ( 2x+3)$.
Hence, the factors of the given equation are $(x+2)$ and $( 2x+3)$.
Let us factorize the quadratic equations using the ac method factoring formula.
Example 1: Factorize the following quadratic trinomial equations:
- $5x^{2} – 8x – 4$
- $x^{2} – 6x + 9$
- $3x^{2} + 6x – 9$
- $7x^{2}+ 16x + 4$
Solution:
1).
$5x^{2} – 8x – 4$
$A = 5$ and $C = -4$
$AC = 5 \times (-4) = -20$
$B = -8$
The next step is to find the two factors which, when multiplied, give the answer as $-20$. The factors can be:
$P = -2 $, $Q = 10$, $-20 = (-2) (10)$
$P = 10 $, $Q = -2$, $-20 = (10) (-2)$
$P = -2 $, $Q = 10$, $-20 = (-2) (10)$
$P = -5 $, $Q = 4$, $-20 = (-5) (4)$
$P = 4 $, $Q = -5$, $-20 = (4) (-5)$
$P = -4$ , $Q = 5$, $-20 = (-4) (5)$
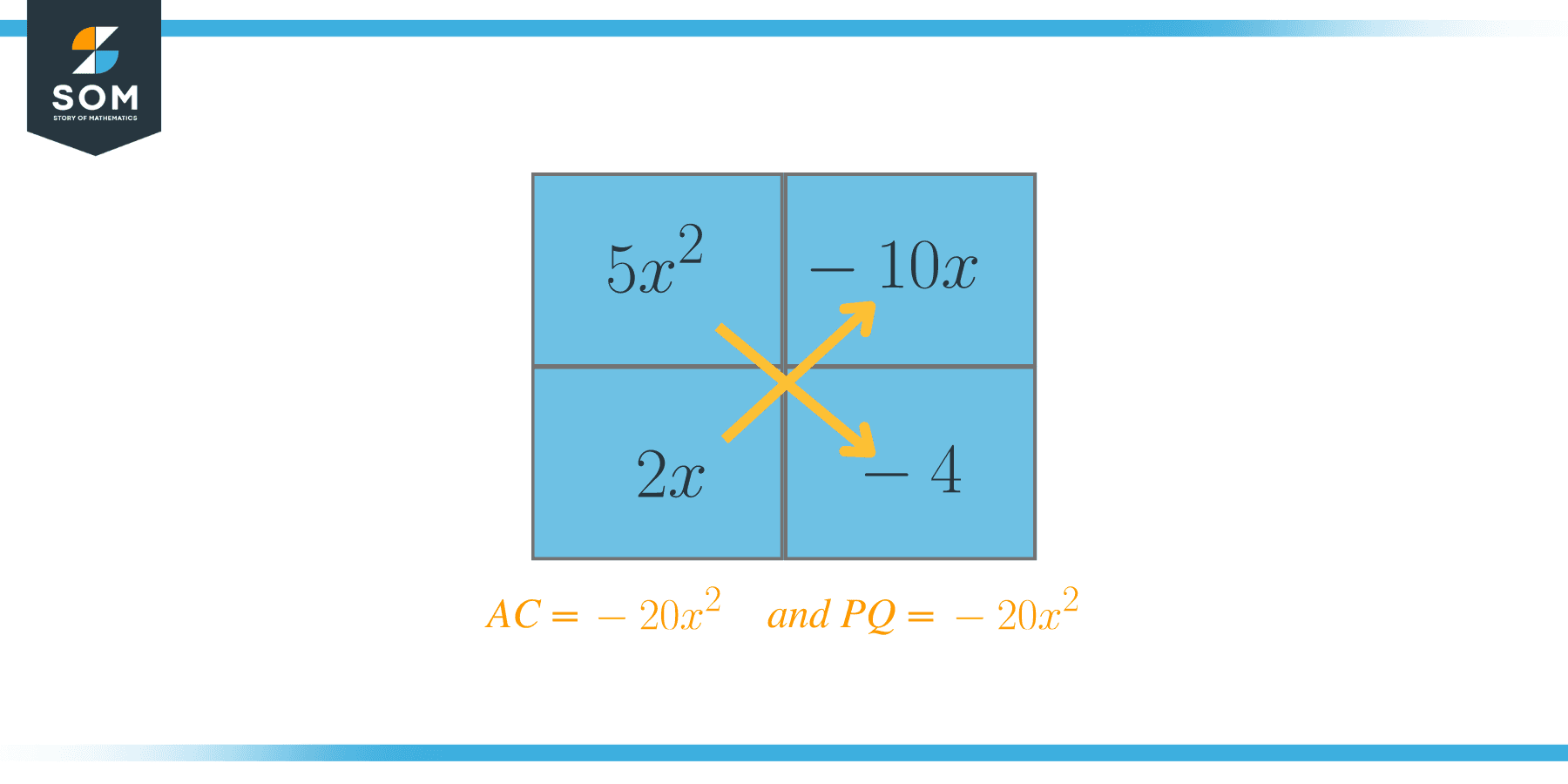
Now we will choose the two factors which, when added together, should be equal to $B = -8$. In this case, those factors are $P = -10$ and $Q = 2$. Now we will rewrite the equation as:
$5x^{2} – 10x + 2x – 4$
$2x ( x – 2) + 2 ( x – 2)$
$(x – 2) (2x+ 2)$.
Hence, the factors of the given equation are 4(x – 2)$ and 4(2x + 2)$.
2).
$x^{2} – 6x + 9$
$A = 1$ and $C = 9$
$AC = 1 \times 9 = 9$
$B = -6$
The next step is to find the two factors which, when multiplied, give the answer as 9. The factors can be:
$P = 3$ , $Q = 3$, $9 = (3) (3)$
$P = -3$ , $Q = -3$, $12 = (-3) (-3)$
$P = 9 4, $Q = 1$, $9 = (9) (1)$
$P = -9$ , $Q = -1$, $9 = (-9) (-1)$
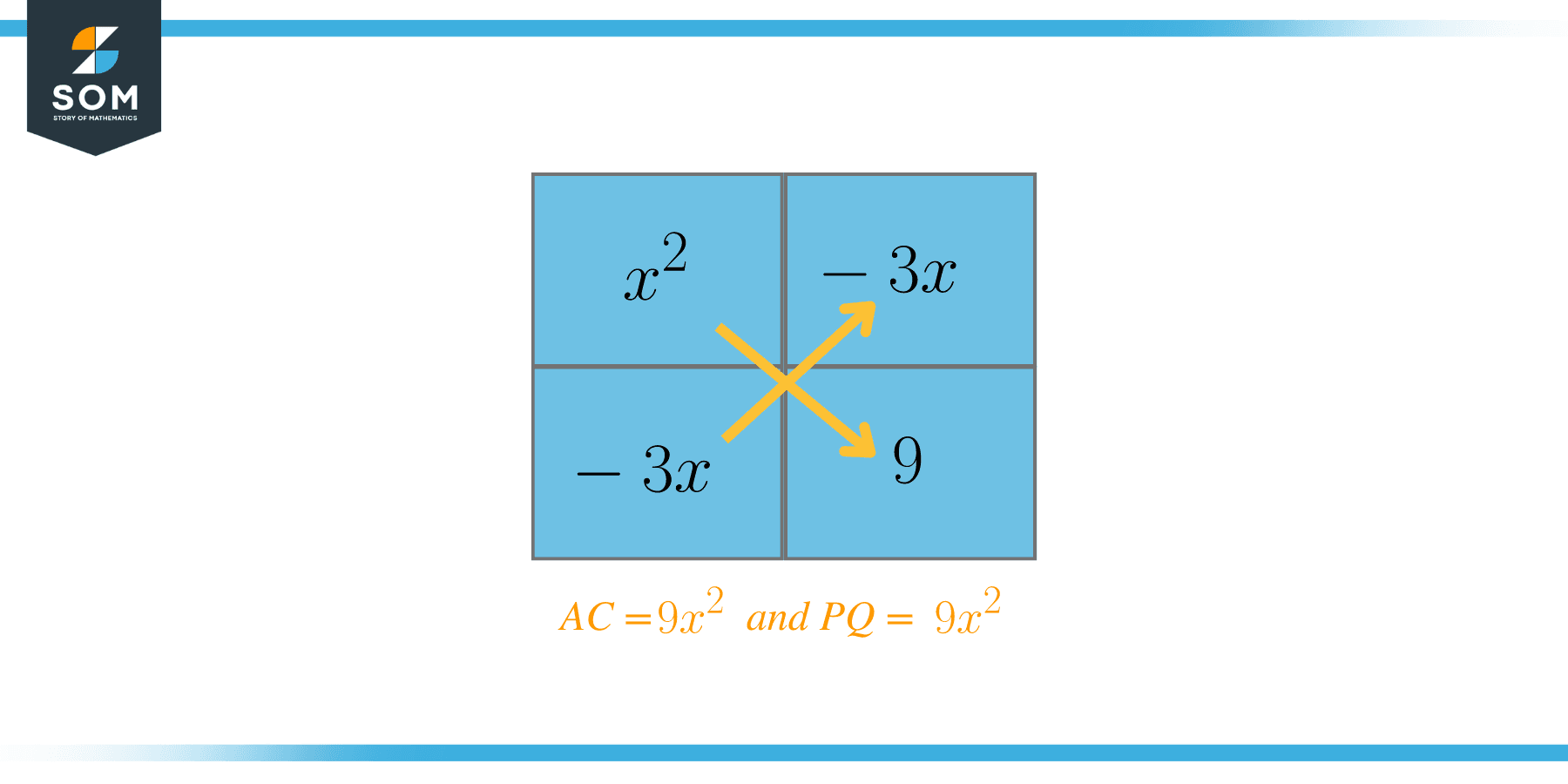
Now we will choose the two factors which, when added together, should be equal to $B = -6$. In this case, those factors are $P = -3$ and $Q = -3$. Now we will rewrite the equation as:
$x^{2} – 3x – 3x + 9$
$x ( x – 3) – 3 ( x – 3)$
$(x – 3) ( x – 3)$.
Hence, this quadratic trinomial has only one factor $(x-3)$. Solving quadratic equations having a two squares number at the end will always yield a common factor.
The given equation is basically a trinomial square equation; we can write it $x^{2} – 6x + 9$ as $x^{2}-6x + 3^{2}$, which, in turn, is equal to $(x – 3)^{2}$. So if an equation is a quadratic trinomial square, then it will have common factors.
3).
$3x^{2} + 6x – 9$
$A = 3$ and $C = -9$
$AC = 3 \times -9 = -27$
$B = 6$
The next step is to find the two factors which, when multiplied, give the answer as $-18$. The factors can be:
$P = -9 $, $Q = 3$, $-27 = (-9) (3)$
$P = -3$ , $Q = 9$, $-27 = (-3) (9)$
$P = -27$ , $Q = 1$, $-27 = (-27) (1)$
$P = 27 $, $Q = -1$, $-27 = (27) (-1)$
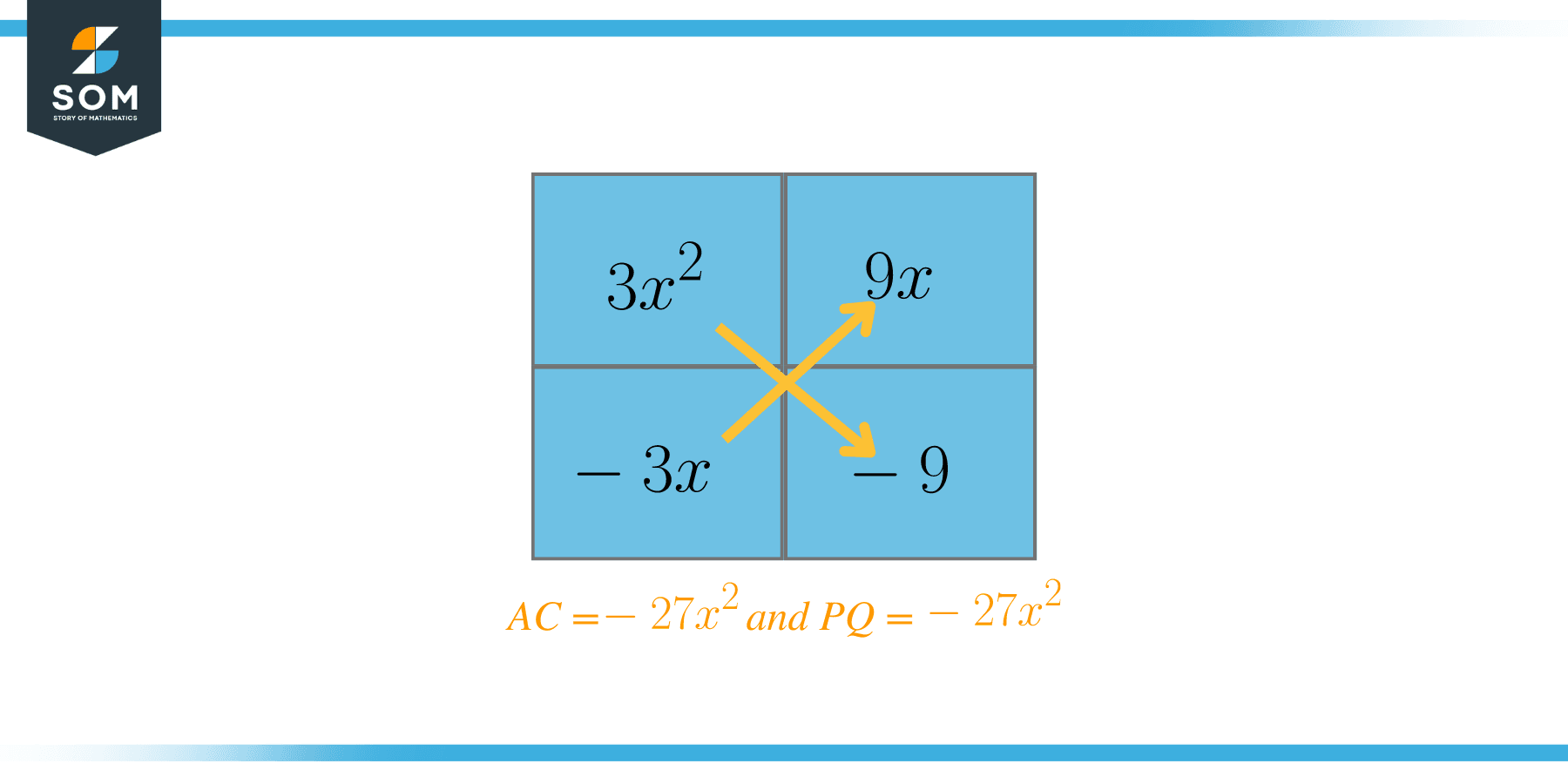
Now we will choose the two factors which, when added together, should be equal to $B = 6$. In this case, those factors are $P = 9$ and $Q = -3$. Now we will rewrite the equation as:
$3x^{2} + 9x – 3x – 9$
$3x ( x + 3) – 3 (x + 3)$
$(x + 3) (3x – 3)$.
Hence, the factors of the given equation are $(x + 3)$ and $(3x – 3)$.
4).
$7x^{2} + 16x + 4$
$A = 7$ and $C = 4$
$AC = 7 \times 4 = 28$
$B = 16$
The next step is to find the two factors which, when multiplied, give the answer of $28$. The factors can be:
$P = 7$ , $Q = 4$, $28 = (7) (4)$
$P = -7$ , $Q = -4$, $28 = (-7) (-4)$
$P = 14 $, $Q = 2$, $28 = (14) (2)$
$P = -14 $, $Q = -2$, $28 = (-14) (-2)$
$P = 28$ , $Q = 1$, $28 = (28) (1)$
$P = -28$ , 4Q = -1$, $28 = (-28) (-1)$
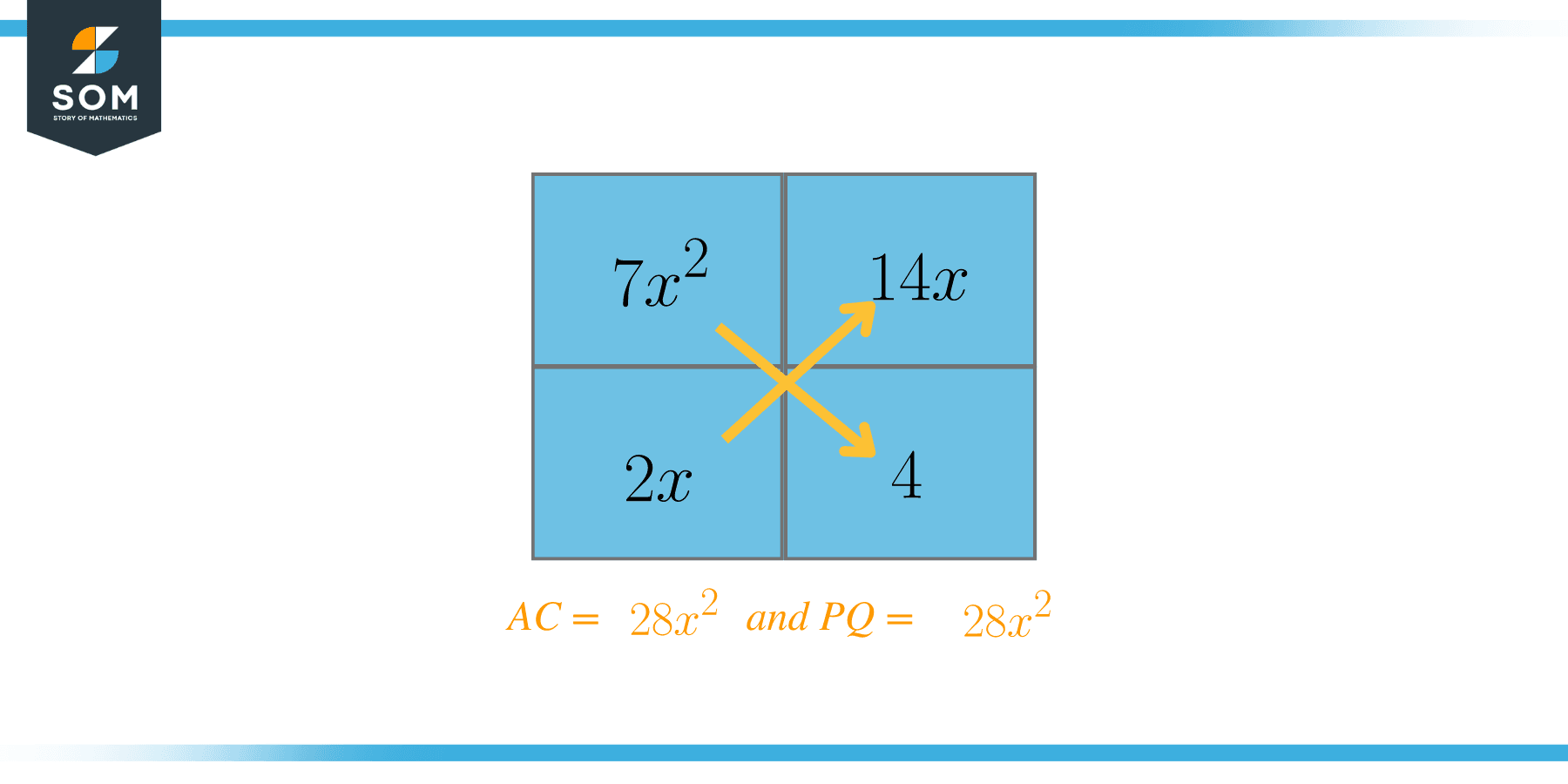
Now we will choose the two factors which, when added together, should be equal to $B = 16$. In this case, those factors are $P = 14$ and $Q = 2$. Now we will rewrite the equation as:
$7x^{2} + 14x + 2x + 4$
$7x ( x + 2) + 2 (x +2)$
$(x+2) ( 7x + 2)$.
Hence, the factors of the given equation are $(x+2)$ and $( 7x + 2)$.
Example 2: If you are given a quadratic equation $2x^{2} – 7x + C$, the value of factors $P$ and $Q$ are $-4x$ and $-3x$, respectively. You are required to determine the value of”“”” by using the AC method.
Solution:
We know that the factors of the equation are -4x and -3x, and their product should be equal to the product of AC.
$-4x \times -3x = 2x \times C$
$12x^{2} = 2x \times C$
$C = \dfrac{12x^{2}}{2x} = 6x$
Example 3: If you are given a quadratic equation $Ax^{2} – 5x + 2$, the value of factors P and Q are $-8x$ and $3x$, respectively. You are required to determine the value of”“”” by using the AC method.
Solution:
We know that the factors of the equation are $-8x$ and $3x$, and their product should be equal to the product of AC.
$-8x \times 3x = A \times 2$
$-24x^{2} = 2A$
$A = \dfrac{-24x^{2}}{2} = -12x^{2}$
Practice Questions:
- Factorize the quadratic terminal equation $8x^{2} – 10x – 3$.
- Factorize the quadratic terminal equation $18x^{2} +12x + 2$.
Answer Key:
1).
$8x^{2} – 10x – 3$
$A = 8$ and $C = -3$
$AC = 8 \times (-3) = -24$
$B = -10$
The next step is to find the two factors which, when multiplied, give the answer as $-24$. The factors can be:
$P = -6$ , $Q = 4$, $-24 = (-6) (4)$
$P = -8 $, $Q = 3$, $-24 = (-8) (3)$
$P = -12$ , $Q = 2$, $-24 = (-12) (2)$
Now we will choose the two factors which, when added together, should be equal to $B = -10$. In this case, those factors are $P = -12$ and $Q = 2$. Now we will rewrite the equation as:
$8x^{2} – 12x + 2x – 3$
$4x (2x – 3) + 1 (2x – 3)$
$(2x – 3) (4x+ 1)$.
Hence, the factors of the given equation are $(2x – 3)$ and $(4x + 1)$.
2).
$18x^{2} + 12x + 2$
$A = 18$ and $C = 2$
$AC = 18 \times (2) = 36$
$B = 12$
The next step is to find the two factors which, when multiplied, give the answer as $36$. The factors can be:
$P = 6 $, $Q = 6$, $36 = (6) (6)$
$P = -6$ , $Q = -6$, $36 = (-6) (-6)$
$P = 9 $, $Q = 4$, $36 = (9) (4)$
$P = -9 $, $Q = -4$, $36 = (-9) (-4)$
$P = 18$ , Q = 2, 36 = (18) (2)
$P = -18$ , $Q = -2$, $36 = (-18) (-2)$
Now we will choose the two factors which, when added together, should be equal to $B = 12$. In this case, those factors are $P = 6$ and $Q = 6$. Now we will rewrite the equation as:
$18x^{2} + 6x + 6x + 2$
$3x (6x + 2) + 1 (6x + 2)$
$(6x + 2) (3x+ 1)$.
Hence, the factors of the given equation are $(6x + 2)$ and $(3x + 1)$.
