Limit of a Series – Definition, Properties, and Applications

The limit of a series is a fundamental concept in mathematical analysis that provide insights into the behavior and convergence of sequences.

This article dives into the intricacies of the limit of a series, investigating the patterns that determine whether a series converges to a finite value or diverges to infinity.

By examining the foundations of series analysis and notable convergence tests, we unravel the captivating world of the limits of a series and their significance in mathematical exploration.

Definition of Limit of a Series

The limit of a series refers to the value that a series approaches as the number of terms in the series tends towards infinity.

In mathematical terms, given a series ∑(aₙ), the limit of the series, denoted as lim(n→∞) ∑(aₙ) or simply lim ∑(aₙ), represents the value towards which the partial sums of the series converge as more and more terms are added. If the limit exists and is a finite value, the series is said to converge.

On the other hand, if the limit does not exist or is infinite, the series is said to diverge. The concept of series limits is crucial in understanding the behavior and properties of series, enabling mathematicians to analyze and make predictions about the behavior of mathematical constructs involving infinite sums. Below we present a generic example representing the limit of series representation in figure-1.

Figure-1.

Historical Significance 

The historical background of the limit of a series dates back to ancient Greek mathematics, with notable contributions from mathematicians such as Zeno of Elea and Archimedes. Zeno’s paradoxes presented philosophical and mathematical challenges related to the concept of infinity and the idea of dividing a distance or time into infinitely many parts.

These paradoxes raised questions about the nature of limits and the possibility of summing an infinite number of terms.

Archimedes, in the 3rd century BCE, made significant advancements in understanding the limit of a series. He employed a method known as the method of exhaustion, which involved approximating a geometric figure by inscribing and circumscribing polygons with increasing numbers of sides.

By refining these approximations, Archimedes could determine the limit of the series representing the area or volume of the figure, establishing the foundations of calculus and the notion of a limit.

During the Renaissance, mathematicians such as Nicolas Oresme and Simon Stevin made further contributions to the understanding of limits. Oresme explored the concept of limits in his work on infinitesimals, laying the groundwork for the development of calculus.

Stevin introduced the idea of a “limiting value” or “approach value” in his work on decimal representation, recognizing the importance of the limiting behavior of numbers as they approach infinity.

The modern formalization of the concept of limits and the rigorous development of calculus took place in the 17th and 18th centuries. Mathematicians such as Isaac Newton and Gottfried Wilhelm Leibniz developed the foundational principles of calculus, including the concept of limits, as part of their independent work on the subject.

Their work provided a rigorous framework for understanding and manipulating infinite processes and laid the groundwork for the development of mathematical analysis.

Properties of Limit of a Series

The limit of a series possesses several important properties that aid in understanding and manipulating the series. Here, we discuss the key properties of the limit of a series in detail.

Linearity

The limit of a linear combination of series is equal to the linear combination of their limits. Mathematically, if lim(n→∞) ∑(aₙ) = L and lim(n→∞) ∑(bₙ) = M, then for any constants c and d, lim(n→∞) ∑(caₙ + dbₙ) = cL + dM. This property allows for the manipulation and combination of series limits.

Additivity

The limit of the sum or difference of two series is the sum or difference of their limits. In other words, if lim(n→∞) ∑(aₙ) = L and lim(n→∞) ∑(bₙ) = M, then lim(n→∞) ∑(aₙ ± bₙ) = L ± M. This property allows for the evaluation of the limit of a series involving arithmetic operations.

Scalar Multiplication

The limit of a series multiplied by a constant is equal to the product of the constant and the limit of the series. Mathematically, if lim(n→∞) ∑(aₙ) = L, then for any constant c, lim(n→∞) ∑(caₙ) = cL. This property enables the scaling of series limits.

Boundedness

If a series is bounded, meaning that its terms are always within a specific range, then the series converges. Boundedness is a sufficient condition for convergence, but not a necessary one. If the terms of a series are unbounded, the series may still converge or diverge.

Monotonicity

If a series is monotonic, either monotonically increasing or monotonically decreasing, and bounded, then the series converges. This property is known as the Monotone Convergence Theorem and provides a convenient way to establish convergence for certain types of series.

Subseries

If a series converges, any subseries (a series formed by selecting a subset of terms from the original series) also converge, and their limits are the same. This property allows for the study of convergence by focusing on subsequences or specific terms of a series.

Comparison Test

If the terms of a series are non-negative, and the terms of another series are always greater or equal to the terms of the first series, then if the second series converges, the first series also converges.

Similarly, if the terms of another series are always smaller or equal to the terms of the first series, and the first series diverges, the second series also diverges. This property, known as the Comparison Test, allows for determining convergence or divergence by comparing series.

Limit Laws

The limit of a series obeys various limit laws, including the laws of arithmetic operations, exponential functions, logarithmic functions, and trigonometric functions. These limit laws enable the evaluation of series limits involving different mathematical functions.

Applications

The limit of a series finds numerous applications across various fields, playing a fundamental role in understanding and analyzing mathematical and real-world phenomena. Let’s explore some key applications of series limits:

Calculus

The concept of series limits is central to calculus, particularly in the study of functions, derivatives, and integrals. The Taylor series, which represents a function as an infinite sum of terms, relies on the limit of a series to approximate functions and perform calculations.

Series limits enable mathematicians to understand the behavior of functions, determine convergence or divergence, and evaluate integrals using techniques like the Riemann sum.

Physics

Series limits are extensively utilized in physics to model and analyze various physical phenomena. For example, in classical mechanics, the concepts of position, velocity, and acceleration can be represented as series expansions using the limit of a series.

Additionally, series limits are employed in quantum mechanics, statistical mechanics, and other branches of physics to describe wave functions, energy levels, and statistical distributions.

Engineering

Engineers rely on series limits for calculations involving electrical circuits, signal processing, control systems, and more. The Fourier series, an expansion of a periodic function into a series of sines and cosines, employs the concept of series limits to decompose complex signals into simpler components.

This decomposition allows engineers to analyze and manipulate signals efficiently in various applications, such as image processing, telecommunications, and audio compression.

Financial Mathematics

Series limits are applied in financial mathematics to model and analyze investment portfolios, compound interest, and financial derivatives. The concept of present value and future value calculations involves series limits, enabling investors and financial analysts to assess the worth of investments over time and make informed decisions.

Computer Science

Series limits have applications in computer science algorithms and computational techniques. For instance, in numerical methods, series expansions are used to approximate solutions to differential equations, integrals, and optimization problems. Additionally, series limits play a role in algorithms for data compression, signal processing, and machine learning.

Probability and Statistics

Series limits are employed in probability theory and statistics to study the behavior of random variables, probability distributions, and statistical estimators. Series expansions, such as the binomial series and Taylor series, are utilized to approximate probability distributions and evaluate statistical functions.

Economics

Series limits are applied in economic modeling and forecasting. Economists use series expansions to approximate economic variables and analyze the behavior of economic systems. Time series analysis, which involves examining patterns and trends in sequential data, relies on series limits to model and predict economic variables over time.

Natural Sciences

The limit of a series is utilized in various scientific disciplines, such as biology, chemistry, and astronomy, to analyze and model natural phenomena. From population dynamics to chemical reactions and celestial mechanics, series limits provide insights into the behavior and evolution of complex systems.

Exercise 

Example 1

Find the limit of the series ∑(1/n) as n approaches infinity.

Solution

To find the limit of the series, we can use the concept of harmonic series. The harmonic series ∑(1/n) is a well-known series that diverges.

As n approaches infinity, the terms of the series become smaller and smaller, but the sum of the terms grows without bounds. Therefore, the limit of the series is infinite. The graphical representation is given below.

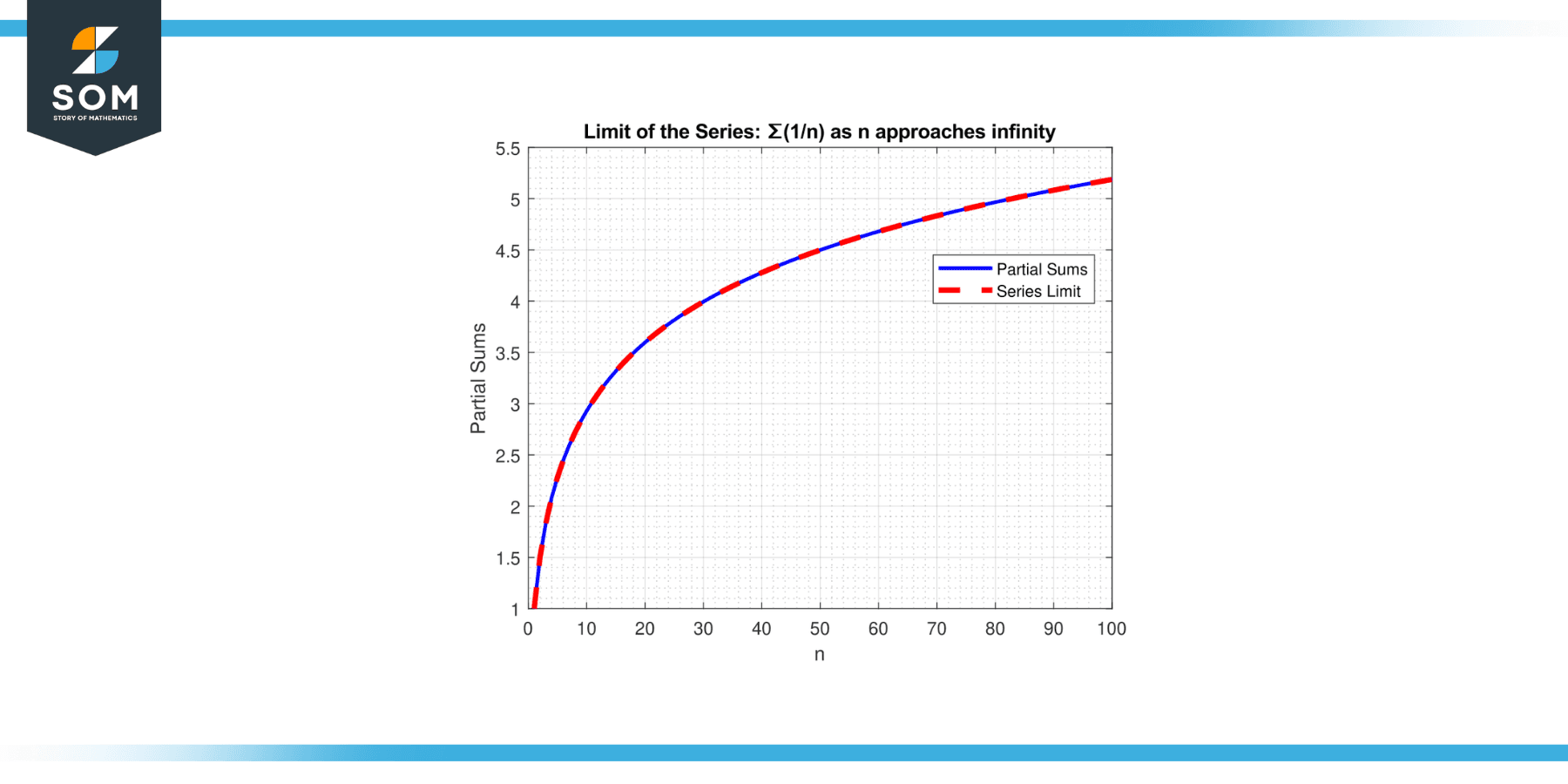
Figure-2.

Example 2

Determine the limit of the series ∑(1/2ⁿ) as n approaches infinity.

Solution

To find the limit of the series, we observe that the series ∑(1/2ⁿ) is a geometric series with a common ratio of 1/2. The formula for the sum of an infinite geometric series is a/(1 – r), where a is the first term and r is the common ratio. In this case, a = 1 and r = 1/2. Applying the formula, we find that the limit of the series is 2.

The graphical representation is given below.

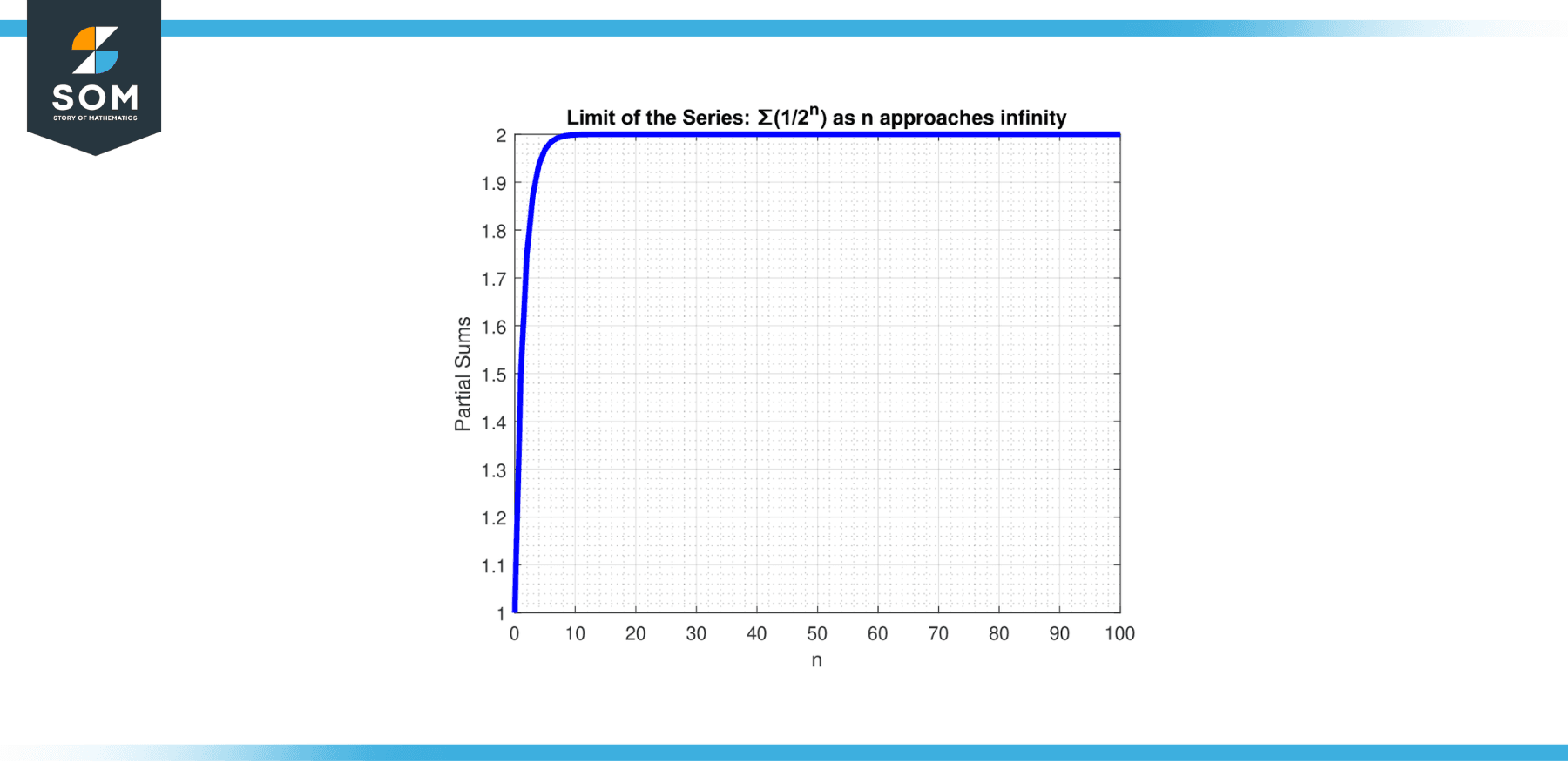
Figure-3.

Example 3

Calculate the limit of the series ∑(n/(n² + 1)) as n approaches infinity.

Solution

To evaluate the limit, we can simplify the series by dividing the numerator and the denominator by n. This gives us ∑(1/(n + 1/n)). As n approaches infinity, the term 1/n approaches 0, so the series simplifies to ∑(1/n). We know from the previous problem that the limit of this series is infinity. Therefore, the limit of the given series is also infinite.

Example 4

Find the limit of the series ∑((2n + 1)/(3n – 2)) as n approaches infinity.

Solution

To determine the limit, we divide the numerator and the denominator by n. This simplifies the series to ∑((2 + 1/n)/(3 – 2/n)). As n approaches infinity, the terms 1/n approach 0, so the series simplifies to ∑(2/3). Since this is a constant term that does not depend on n, the limit of the series is simply 2/3.

Example 5

Calculate the limit of the series ∑(n²/3ⁿ) as n approaches infinity.

Solution

To find the limit, we can use the ratio test for series convergence. Taking the ratio of consecutive terms, we have (n+1)²/$3^{n+1}$ * 3ⁿ/n². Simplifying further, we get (n+1)²/(3n²). As n approaches infinity, this ratio approaches 1/3. Since the ratio is less than 1, the series converges. Therefore, the limit of the series is 0.

Example 6

Determine the limit of the series ∑(n!/(nⁿ)) as n approaches infinity.

Solution

To evaluate the limit, we can use the ratio test. Taking the ratio of consecutive terms, we obtain ((n+1)!/$(n+1)^{n+1}$) * (nⁿ)/n!. Simplifying further, we get (n+1)/(n+1) * (n/n)ⁿ. As n approaches infinity, this ratio simplifies to 1/e, where e is the base of the natural logarithm. Since the ratio is less than 1, the series converges. Therefore, the limit of the series is 0.

Example 7

Calculate the limit of the series ∑(sin(1/n)) as n approaches infinity.

Solution

To evaluate the limit, we can use the fact that sin(x)/x approaches 1 as x approaches 0. Applying this to our series, we have sin(1/n)/(1/n). As n approaches infinity, 1/n approaches 0, and the series simplifies to 1. Therefore, the limit of the series is 1.

Example 8

Find the limit of the series ∑($n^{3/2}$/(2ⁿ)) as n approaches infinity.

Solution

To determine the limit, we can use the ratio test. Taking the ratio of consecutive terms, we have ($(n+1)^{3/2}$/($2^{(n+1)}$)) * (2ⁿ)/($n^{3/2}$). Simplifying further, we get $(n+1)^{3/2}$/($2n^{3/2}$). As n approaches infinity, this ratio simplifies to 1/2. Since the ratio is less than 1, the series converges. Therefore, the limit of the series is 0.

 

All images were created with MATLAB.