JUMP TO TOPIC
 The process of integration is considered the reverse of taking the derivative of a function. We can look at integrals in such a way that the function being integrated is the function in its derivative form while the integral of that function is the original function. That is:
The process of integration is considered the reverse of taking the derivative of a function. We can look at integrals in such a way that the function being integrated is the function in its derivative form while the integral of that function is the original function. That is:
\begin{align*}
\int f(x)=F(x)+C
\end{align*}
where
\begin{align*}
\dfrac{d}{dx} F(x)=f(x).
\end{align*}
Other than finding the antiderivatives of a function, some other integration techniques involve integration by substitution, integration by parts, and others. In this article, we will discuss how to evaluate the integral of $1/x$ and other functions of similar or related format using different integration technique.
What Is the Integral of 1/x?
The integral of $1/x$ is $\ln|x|+C$. In symbols, we write:
\begin{align*}
\int\dfrac{1}{x}\, dx=\ln|x|+C,
\end{align*}
where $C$ is a real number and is called the constant of integration.
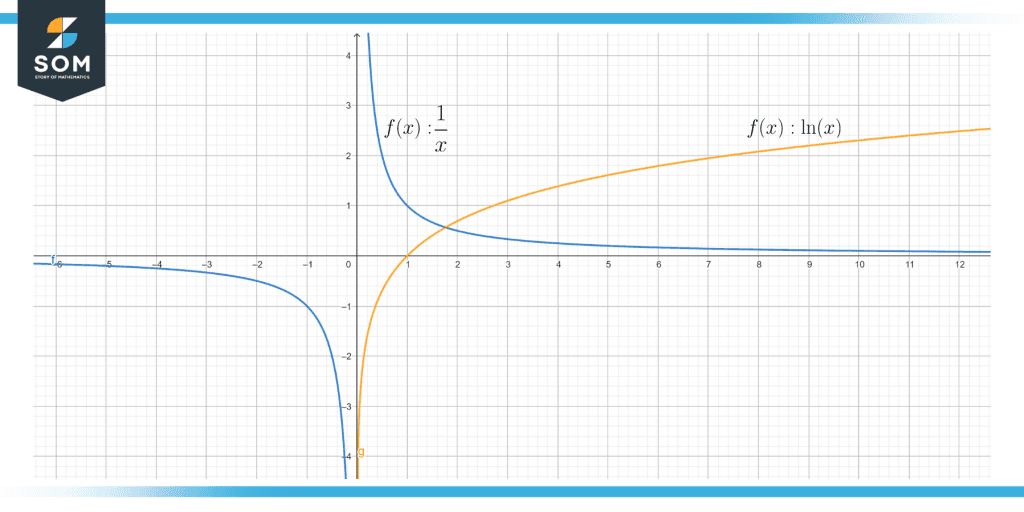
Figure 1 shows the related behavior of the graph of $1/x$ and $\ln x$. The graph in red lines describes the graph of the function $1/x$ while the graph in blue lines portrays the graph of the logarithmic function $\ln x$.
Why Is the Integral of 1/x ln x?
Since we mentioned earlier that integrals are the reverse of derivatives, then we let $f(x)=1/x$. So that we have:
\begin{align*}
\int\dfrac{1}{x}\,dx=F(x)+C,
\end{align*}
where:
\begin{align*}
\dfrac{d}{dx} F(x)=\dfrac{1}{x}.
\end{align*}
Note that the derivative of $\ln x$ is $1/x$. Thus, it follows that:
\begin{align*}
\dfrac{d}{dx} \ln x=\dfrac{1}{x},
\end{align*}
then:
\begin{align*}
\int\dfrac{1}{x}\, dx=\ln x+C.
\end{align*}
However, we will notice that the only restrictions in the domain of $f’(x)$, which is $x$, must not be equal to $0$. So, in $f’(x)$, $x>0$ or $x<0$, but $x\neq0$. While in the function $\ln x$, the domain is only the positive numbers since natural logarithmic is not defined in negative numbers or in $0$. Hence, $x$ is strictly a positive number.
This follows that $1/x$ and $\ln(x)$ have different domains, which is not okay since they must have the same domain. So we need to consider when $x<0$.
To do this, we need to assume that $x=-u$, where $u$ is a real number. This follows that if $x<0$, then $u>0$. And substituting the value of $x$, we will have $dx=-du$, and this implies that:
\begin{align*}
\int\left(\dfrac{1}{x}\right)\, dx=\int\left(\dfrac{1}{-u}\right)\,\left(-du\right).
\end{align*}
This follows that when $x<0$, then the integral of $f'(x)$ is:
\begin{align*}
\int\left(\dfrac{1}{x}\right)\, dx= \ln (u)+C_1,
\end{align*}
where $C_1$ is an arbitrary constant. And by substituting the value of $u$, we have:
\begin{align*}
\int\left(\dfrac{1}{x}\right)\, dx= \ln (-x)+C_1.
\end{align*}
However, we know that the natural logarithmic is not defined in negative numbers, hence we will use the absolute function, where if $x\geq0$, then $|x|=x$, and if $x<0$, then $|x|=-x$. Therefore, the integral of $1/x$ is $\ln|x|+C$, where $C$ is an arbitrary constant.
Thus, this verifies and explains the integral of $1/x$ proof.
Integration of 1/x With Limits of Integration
Example
- Evaluate the integral $\int_{-1}^2 \dfrac{1}{x}\,dx$.
In this example, the limits of integration is from $-1\leq x\leq2$. Following the formula we obtained earlier, we have:
\begin{align*}
\int_{-1}^2 \dfrac{1}{x}\,dx&=\ln|2|-\ln|-1|=\ln\left|\dfrac{2}{(-1)}\right|\\
&=\ln|-2|\\
&=ln 2.
\end{align*}
Thus, the definite integral $\int_{-1}^2 \dfrac{1}{x}\,dx$ is equal to the real number $\ln2$. This can be interpreted further that the area under the curve of $1/x$ from the interval $-1\leq x\leq2$ is equal to $\ln2$.
Example
- Solve for the integral $\int_0^4 \dfrac{1}{x}\,dx$.
Using the formula above, we have to plug in the limits of integration $0$ and $4$, respectively.
\begin{align*}
\int_0^4 \dfrac{1}{x}\,dx&=\ln|4|-\ln|0|\\
&=\ln\left|\dfrac{4}{0}\right|\\
&=\text{undefined}.
\end{align*}
Note that since $\dfrac{4}{0}$ is undefined, then the whole integral is also undefined. Thus, we cannot have $0$ as one of the limits of integration because $\ln0$ does not exist.
Now, let’s look at the other powers of $1/x$, if they have the same integral as $1/x$.
The Integral of 1/x^2
Evaluate the Integral of 1/x^3
The integral of the function $\dfrac{1}{x^3}$ is $-\dfrac{1}{2x^2}+C$. We verify that this is indeed the integral.
In the previous section, we looked for a function that, when taken, the derivative will give us the function we are integrating. In this case, let’s try a different technique called integration by substitution.
Note that $1/x^3$ can be expressed as:
\begin{align*}
\dfrac{1}{x^3} &=\dfrac{1}{x}\cdot\dfrac{1}{x^2}.
\end{align*}
So that we have:
\begin{align*}
\int \dfrac{1}{x^3}\, dx=\int\dfrac{1}{x}\cdot\left(\dfrac{1}{x^2} \,dx\right).
\end{align*}
We obtained from the previous section that:
\begin{align*}
\dfrac{d}{dx} \dfrac{1}{x}=-\dfrac{1}{x^2}.
\end{align*}
So, if we let $u=\dfrac{1}{x}$, then:
\begin{align*}
\dfrac{du}{dx} &=\dfrac{d}{dx} \dfrac{1}{x}\\
\Rightarrow \dfrac{du}{dx} &=-\dfrac{1}{x^2}\\
\Rightarrow du&=-\dfrac{1}{x^2}\, dx\\
\Rightarrow -du&=\dfrac{1}{x^2}\, dx.
\end{align*}
We go back to the initial integral and substitute $u=1/x$ and $-du=1/x^2\, dx$ into the expression. Thus, we have:
\begin{align*}
\int\dfrac{1}{x^3}\,dx &=\int\dfrac{1}{x}\cdot\left(\dfrac{1}{x^2}\,dx\right)\\
&=\int u\cdot\left(-du\right)\\
&=-\int u\,du\\
&=-\dfrac{u^2}{2}+C.
\end{align*}
Since our initial variable is $x$, then we substitute back the value of $u$ in the integral we obtained.
\begin{align*}
\int\dfrac{1}{x^3}\,dx&=-\dfrac{u^2}{2}+C\\
&=-\dfrac{\left(\dfrac{1}{x}\right)^2}{2}+C\\
&=-\dfrac{1}{2x^2}+C.
\end{align*}
Thus, it is true that:
\begin{align*}
\int\dfrac{1}{x^3}\, dx=-\dfrac{1}{2x^2} +C.
\end{align*}
Some Observations
We observe that the integral of $1/x$ is different from the integral of other powers of $1/x$. Moreover, we can observe that the integral exists for all $x$ except for $x=0$. This is due to the fact that $1/x$ and $\ln|x|$ is not defined at $x=0$.
For the case of powers $1/x$, we can generalize their integrals using the formula:
\begin{align*}
\int\left(\dfrac{1}{x}\right)^n\,dx=\int\left(\dfrac{1}{x^n}\right)\,dx=-\dfrac{1}{\left(n-1\right)x^{n-1}}+C,
\end{align*}
where $n\neq1$.
Example
- Find the integral of $\dfrac{1}{x^5}$.
We use the generalized formula for the powers of $1/x$ to find the integral of $1/x^5$. We take $n=5$. Thus, we have:
\begin{align*}
\int\dfrac{1}{x^5}\,dx&=-\dfrac{1}{(5-1) x^{5-1}}+C\\
&=-\dfrac{1}{4x^4}+C.
\end{align*}
Therefore, the integral of $\dfrac{1}{x^5}$ is $-\dfrac{1}{4x^4}+C$.
Conclusion
In this article, we discussed the integral function and focused on evaluating the integral of $1/x$ and its powers. Here are the important points we got from this discussion.
- The integral of $\dfrac{1}{x}$ is equal to $\ln|x|+C$.
- The definite integral $\int_a^b \dfrac{1}{x}\,dx$ can be simplified to $\ln\left|\dfrac{b}{a}\right|$, where $a$ and $b$ are nonzero real numbers.
- The definite integral of $1/x$ is undefined whenever one of the limits of integration is zero.
- The generalized formula for the integral of the powers of $\dfrac{1}{x}$ is $\int\dfrac{1}{x^n}\,dx=\dfrac{1}{\left(n-1\right) x^{n-1}}+C$.
It is important to know how to evaluate the integral of $1/x$ because it is not like other functions that follow a certain formula to find its integral, as it is dependent on its antiderivative $\ln x$. Moreover, in evaluating integrals and definite integrals of $1/x$, it is important to take note of the restrictions of the domains of the given functions.
