JUMP TO TOPIC
To find all the real square roots of – 9/16, first, pay attention to the negative sign in the fraction, and note that negative numbers do not have real square roots. Thus, the answer to this problem is that – 9/16 does not have real square roots. Let’s find out why – 9/16 does not have real roots and how we solve other root-finding problems involving fractions. For simplicity, when the context is clear, we use the term “roots” to simplify the expression “square roots”.
- 9/16 Does Not Have Real Roots
Note that – 9/16 does not have real roots because it is a negative fraction. Only nonnegative real numbers have real roots. In the case of negative real numbers, they have imaginary roots. The square root of – 1 is equal to the imaginary unit i. Thus, in general, negative real numbers have imaginary roots multiplied by i, denoting that a root is an imaginary number.
Likewise, in the case of negative fractions, they do not have real roots, but what they do have are imaginary roots. Thus, in finding all the real roots of – 9/16, the answer is it that doesn’t have any real roots. But, if we are only concerned with finding any root of – 9/16, it has imaginary roots which are positive and negative ¾ i. Read in the next sections how we arrive with ¾ i and – ¾ i as roots of – 9/16 by solving the roots of the positive fraction 9/16.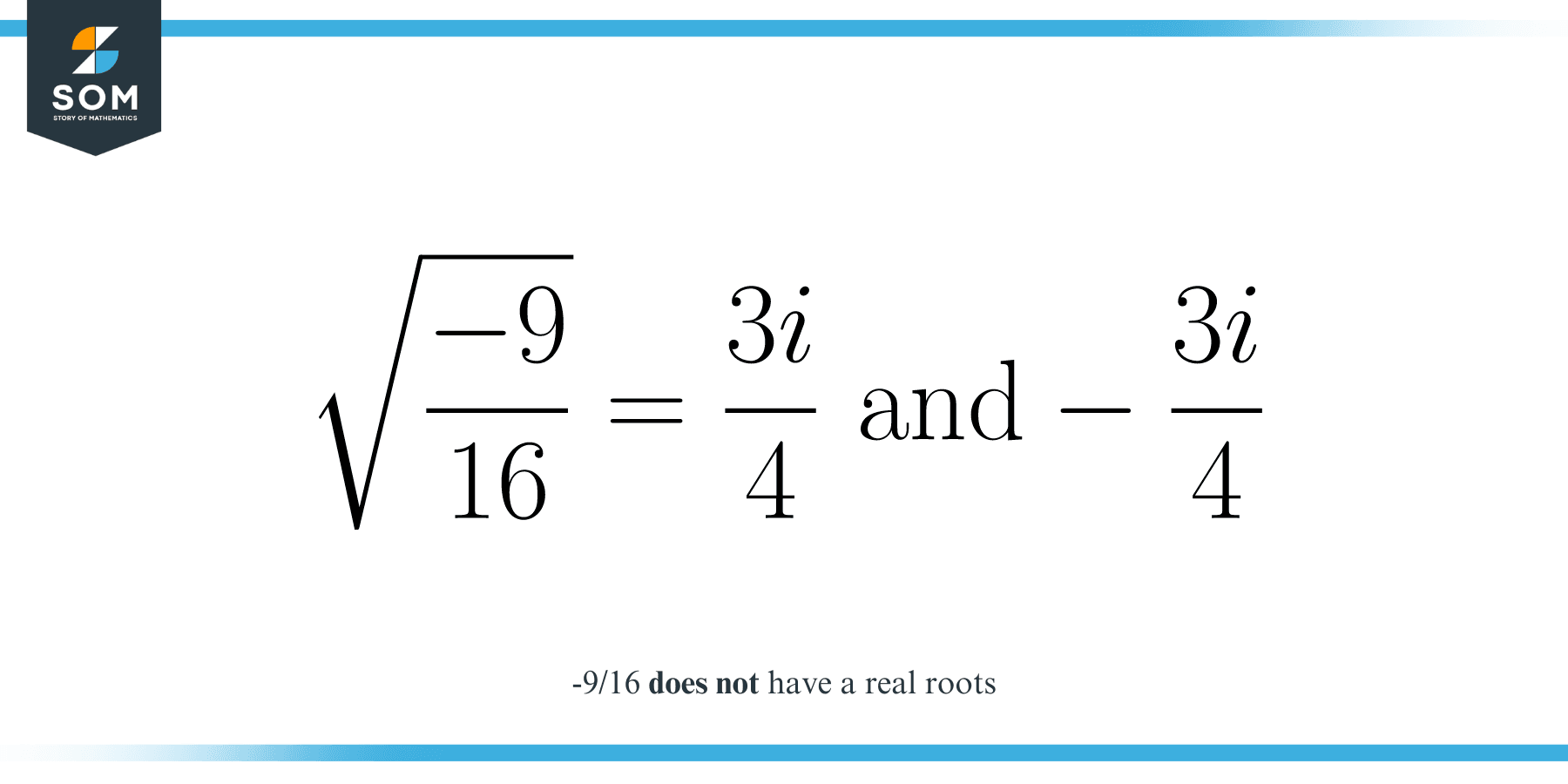
Real Roots of a Fraction
The principal square root of a given fraction is the resulting fraction from taking the root of the numerator and denominator. The numerator of the square root of a fraction is the root of the numerator of the fraction. In a similar manner, the denominator of the square root of the fraction is the root of the denominator of the fraction. If we express it using mathematical symbols and expressions, then we have $\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}$.
The complete real roots of a fraction are the positive and the negative principal square root of the fraction.
Example
Solve and determine whether the square root of 9/16 rational or irrational.
- The numerator is 9 and its principal root is 3.
- The denominator is 16 and its principal root is 4.
- The principal square root fraction of 9/16 is 3/4.
- All the real roots of 9/16 are 3/4 and – 3/4.
- The roots of 9/16 are rational.
Is 9/16 Considered a Perfect Square?
Yes, 9/16 is a perfect square because the real roots of 9/16 are both rational. The numerator 9 is the square of 3 and the denominator 16 is the square of 4.
A fraction is a perfect square when its numerator and denominator are both squares of an integer. This means that the fraction is a square of another rational number, that is, its numerator and denominator are both integers.
Thus, we can guarantee that the square root of a fraction is also a fraction. For example, 5 is not a square of any number. This is because we cannot find any integer that when multiplied by itself will give us 5. However, 5 still has a square root of approximately 2.236 but since it is not an integer then the square of 2.236 will not equate to 5.
In the case of fractions whose real roots have denominators that are not integers, we need to rationalize the denominator to remove the radical sign. You can find a complete discussion of this topic here.
FAQ
If you have more questions or need extra information, check common questions concerning a square root to find the answers.
What Are the Roots of 9/16 as a Decimal?
The roots in decimal are 0.75 and – 0.75. Since ¾ is the principal root of 9/16, it can be transformed into a decimal by dividing 3 by 4.
Is There a Square Root for Every Number?
It depends on what type of roots you want to get. If you only want real roots, then the answer is no since only nonnegative real numbers have real roots. But, if you consider imaginary roots as roots, then yes, every number has a root.
How Do I Find the Square Root of Any Number Within Seconds?
The most obvious answer, if you are allowed to use it, is using a calculator to get a very accurate answer, especially if the roots are irrational. There are also other ways to solve or calculate the roots of larger numbers. But, in the case when the number is not large enough you can also memorize the squares of numbers (maybe all the way to 30) to be able to answer within seconds.
Conclusion
We discussed how to find all the real square roots of – 9/16 and how to find the roots of any given fraction. This article further enriched us with the following important points:
- – 9/16 does not have any real roots because it is a negative fraction but it does have imaginary roots $¾ i$ and $– ¾ i$.
- Negative fractions do not have real roots. Their roots are imaginary fractions.
- The complete real roots of a fraction are the positive and negative fractions resulting from taking the roots of the numerator and denominator.
- The roots of a fraction are rational if and only if the numerator and denominator are squares of an integer.
You see that finding the roots of a fraction is not too hard if you know how. So, the next time you come across a problem like this, you will easily solve the root-finding problem of any fraction.