JUMP TO TOPIC
In this comprehensive exploration, we will specifically focus on arctan(0), demystifying its meaning, understanding its mathematical underpinnings, and unveiling its significance in real-world applications.
Definition
The arctan function, also known as the inverse tangent or tan^(-1), is used to find the angle whose tangent is a given number. In other words, it undoes what the tangent function does, bringing you back to the original angle.
When we look at “arctan(0)”, we are seeking the angle whose tangent is 0.
In the context of right triangle trigonometry, the tangent (tan) of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. When this ratio equals 0, it implies that the length of the side opposite the angle is 0, and this occurs when the angle itself is 0 degrees (or 0 radians).
Therefore, arctan(0) = 0 degrees (or 0 radians), using the principal value (the most commonly accepted value). This means that the angle which has a tangent of 0 is 0 degrees or 0 radians.
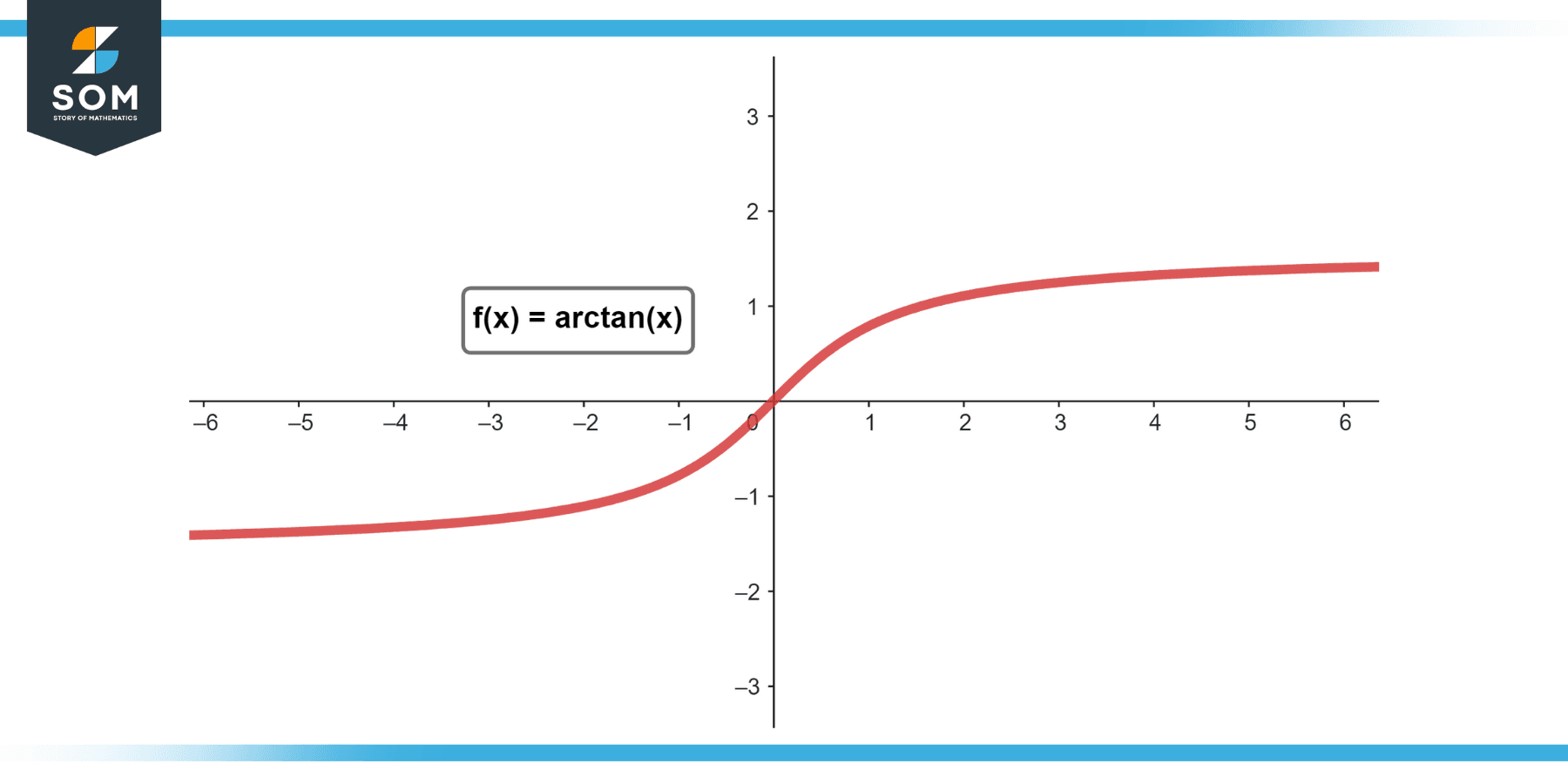Figure-1.
Properties
arctan, or the inverse tangent function, when evaluated at zero, has some interesting properties. Here are the key ones:
Uniqueness
You are correct. The value of arctan(0) is indeed unique. There is only one angle between -90 and 90 degrees (or -π/2 and π/2 radians) that has a tangent of zero, and that angle is 0 degrees (or 0 radians).
Sign
arctan(0) is 0, which is neither positive nor negative.
Periodicity
You are correct. Unlike the tangent function, which is periodic with a period of π radians (or 180 degrees), the arctan function does not repeat when evaluated at 0. This is because there is only one value in its range of -π/2 to π/2 that will return a tangent of 0.
Monotonicity
The arctan function is monotonically increasing in its domain. This means that for every x and y in the domain of arctan such that x < y, arctan(x) < arctan(y). Since 0 is the smallest number in the domain, arctan(0) will indeed be the smallest value in the range of arctan.
Continuity and Differentiability
The arctan function is continuous and differentiable for all real numbers. This means that it has no breaks or jumps in its graph, and it has a derivative at all points, including 0.
Symmetry
The arctan function is indeed an odd function. This means that for every x in the domain of arctan, arctan(-x) = -arctan(x). Since arctan(0) = 0, this property tells us that arctan(-0) = -arctan(0) = -0 = 0. Therefore, the function is symmetric about the origin, exhibiting mirror-image behavior for positive and negative values of its argument.
Limits
As x approaches 0 from the right ($x → 0^+$), arctan(x) also approaches 0. Similarly, as x approaches 0 from the left ($x → 0^-$), arctan(x) also approaches 0. Therefore, the function has a limit at 0, and the limit is 0.
Exercise
Example 1
arctan(0)
Solution
The arctan(0) is equal to 0, as it’s the angle whose tangent is 0.
Example 2
arctan(0) + arctan(0)
Solution
This is equal to 0 + 0 = 0.
Example 3
2*arctan(0)
Solution
This is equal to 2*0 = 0.
Example 4
sin(arctan(0))
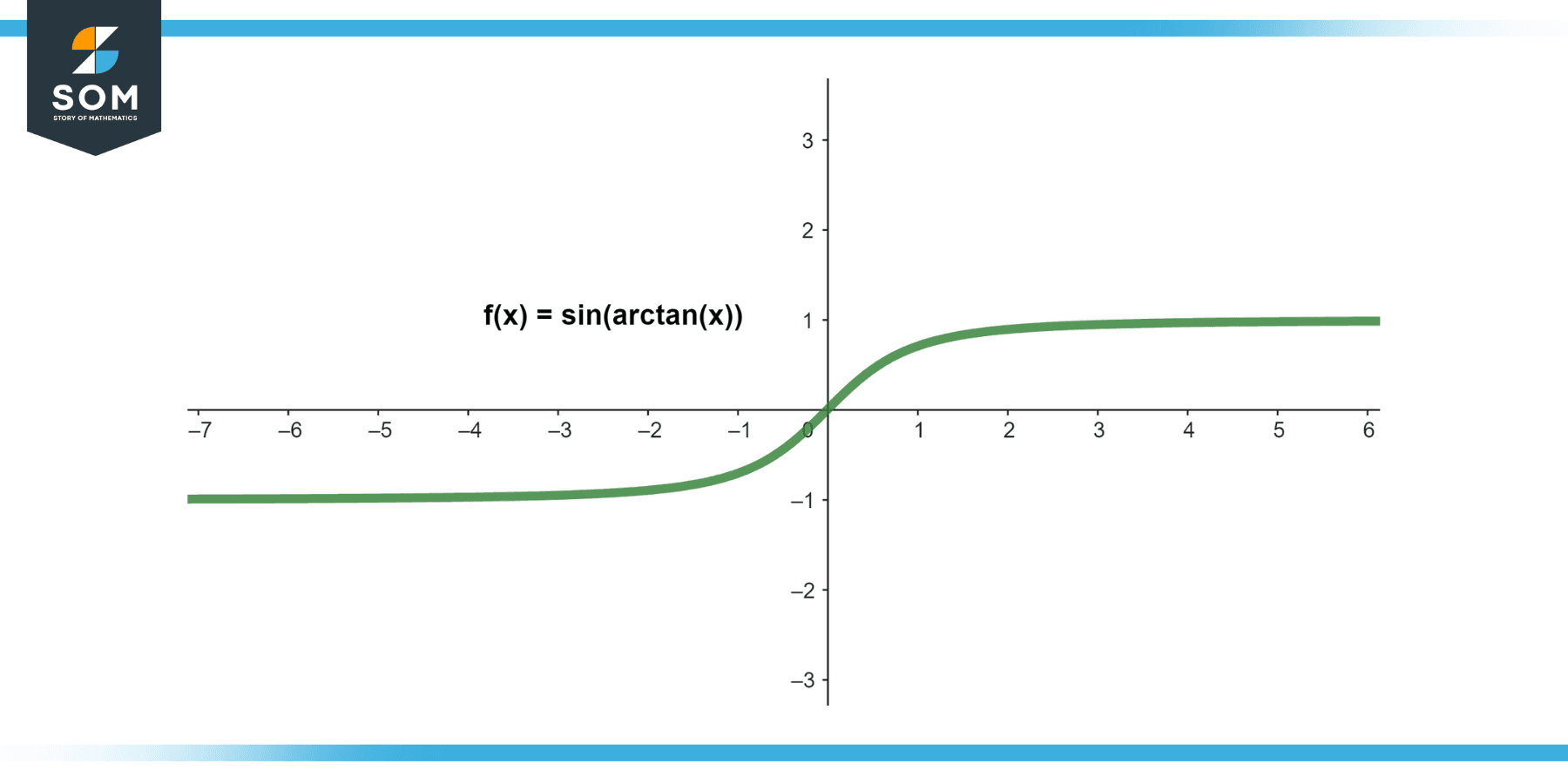
Figure-2.
Solution
Since arctan(0) = 0, the sine of 0 is also 0.
Example 5
cos(arctan(0))
Solution
Here, arctan(0) = 0, and the cosine of 0 is 1.
Example 6
tan(arctan(0))
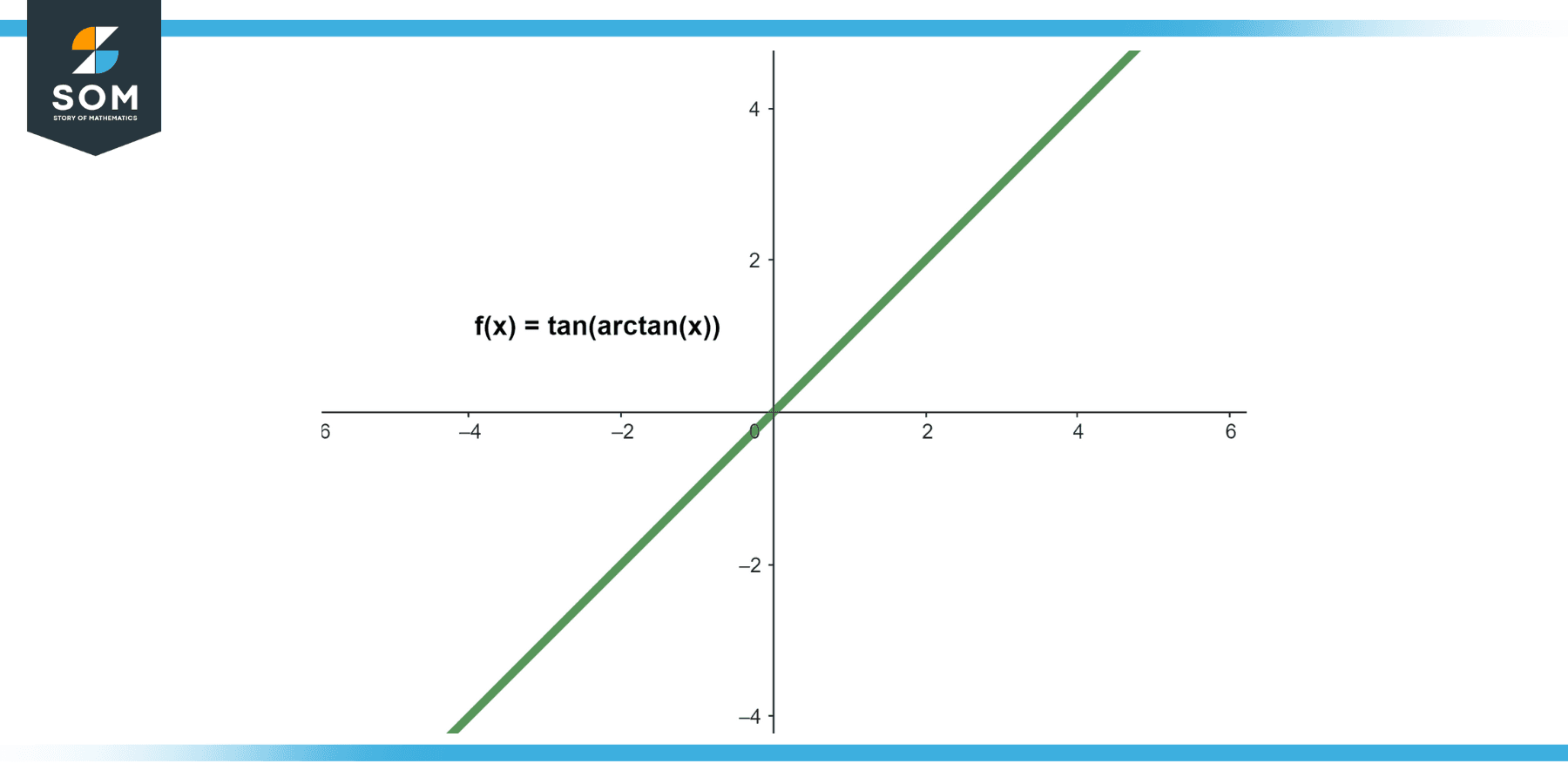
Figure-3.
Solution
The tangent of arctan(0) is simply 0, as arctan(0) = 0.
Example 7
√arctan(0)
Solution
The square root of arctan(0) is √0 = 0.
Example 8
1/arctan(0)
Solution
This operation would be undefined as you cannot divide by zero.
Applications
Geometry and Trigonometry
Here, arctan(0) is fundamentally used to establish the relationship between angles and the ratios of side lengths in right triangles. This principle aids in the analysis of shapes, space, and the relative positions of figures.
Physics
In physics, particularly in areas such as mechanics and electrodynamics, arctan(0) is frequently used. For instance, when calculating angular momentum, torque, or phasor representations of waves, where the angle of rotation is zero, arctan(0) is utilized.
Computer Graphics and Game Development
Computer graphics heavily utilize trigonometric principles for rendering scenes, particularly in 3D space. For example, when an object’s orientation in the scene is parallel to an axis, the angles involved in the rotation calculations would leverage the arctan(0) principle.
Similarly, in game physics, when there’s no angular difference between objects or the gameplay elements, arctan(0) might be used.
Engineering
In fields like civil engineering, mechanical engineering, and electrical engineering, understanding the principles of arctan(0) is crucial, particularly in areas such as signal processing, control systems, stress analysis on materials, and fluid dynamics.
In navigational systems, particularly in aviation and marine contexts, where bearings and headings are often described in angular terms relative to North (defined as 0 degrees or radians), the concept of arctan(0) is implicitly used.
Robotics
In robotics, arctan(0) is used in calculations involving the movement and orientation of robots. When a robot moves directly along the X or Y-axis, the change in angle would be 0, utilizing the principle of arctan(0).
All images were created with GeoGebra.