
Similar triangles proof is a captivating facet of geometry, offering a rich playground for mathematical exploration and proof, embodying the harmony and beauty in the world of shapes and forms. These congruent figures, despite their varying scales, uphold the fundamental principle of similarity: maintaining identical angles while exhibiting proportional sides.
Through this article, we will delve into the intriguing world of similar triangles, traversing diverse paths of proof that reveal their inherent and mesmerizing properties.
These mathematical deductions will illuminate how these identical yet diverse geometric figures elegantly uphold the fascinating and expansive world of geometry, providing a platform for understanding more complex shapes and theorems.
Defining Similar Triangles Proof
Similar triangles are geometric figures that maintain the same shape but can have different sizes. The formal definition of similar triangles is as follows:
Two triangles are similar if their corresponding angles are congruent (equal in measure) and their corresponding sides are proportional in length.
When we talk about “similar triangle proofs,” we’re referring to mathematical proofs that demonstrate the similarity of two triangles. These proofs are based on one of three postulates:
Angle-Angle (AA) Postulate
If two angles of one triangle are congruent to two angles of another, the two triangles are similar.
Side-Angle-Side (SAS) Postulate
If an angle of one triangle is congruent to an angle of a second triangle, and the sides, including these angles, are proportional, then the triangles are similar.
Side-Side-Side (SSS) Postulate
If the corresponding sides of two triangles are proportional, then the triangles are similar.
Example
Given a right triangle ABC with ∠ACB = 90° and AD being the altitude to the hypotenuse (BC), prove that △ABC ~ △BAD ~ △ACD.
Figure-1.
Proof
Firstly, we need to identify the angles in our triangles.
In △ABC, ∠BAC is ∠A and ∠ABC is ∠B.
In △BAD, ∠BAD is ∠A and ∠ABD is equal to ∠C (because ∠ABD and ∠ACB are complementary and ∠ACB = 90°).
In △ACD, ∠ACD is ∠B and ∠ADC is ∠A (because ∠ADC and ∠ADB are complementary and ∠ADB = 90°).
Now we can prove the similarity:
For △ABC and △BAD: They have ∠A in common and ∠ABC = ∠ABD = ∠C. So by the AA (Angle-Angle) criterion, △ABC ~ △BAD.
For △ABC and △ACD: They have ∠B in common and ∠BAC = ∠CAD = ∠A. So by the AA (Angle-Angle) criterion, △ABC ~ △ACD.
Thus, △ABC ~ △BAD ~ △ACD.
The AA postulate states that if two triangles have two corresponding angles that are congruent, then the triangles are similar. This proof illustrates the use of the AA postulate, one of the key methods of proving triangle similarity.
Properties
Following are the properties associated with similar triangles that are often leveraged in proofs:
Corresponding Angles are Congruent
If two triangles are similar, then the measure of their corresponding angles is the same. This is a direct consequence of the Angle-Angle (AA) criterion of triangle similarity.
Corresponding Sides are Proportional
The lengths of corresponding sides in similar triangles maintain the same ratio. For instance, if we have two similar triangles ABC and DEF, the ratio of side AB to side DE is the same as the ratio of side BC to side EF, and the same as the ratio of side AC to side DF.
Proportional Altitudes, Medians, and Angle Bisectors
In two similar triangles, the ratios of corresponding altitudes, medians, or angle bisectors are the same as the ratio of corresponding sides.
Parallel lines and Transversals
If a line parallel to one side of a triangle intersects the other two sides, it divides those sides proportionally, creating similar triangles.
Area Ratio
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Pythagorean Theorem
In a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can often be used in conjunction with similarity properties to prove further similarities or relationships between figures.
Remember, these properties come from the definitions and postulates of similar triangles. Any proof involving similar triangles will most likely make use of one or more of these properties.
Applications
Similar triangles have a wide range of applications across numerous fields. Let’s explore a few:
Engineering and Architecture
Similar triangles are used in the scaling of models. When engineers or architects design buildings or machinery, they often build a scale model first. The real object and its model are similar “triangles” in three dimensions – they have the same shape but different sizes.
Astronomy and Physics
In astronomy, similar triangles are used to calculate distances that would be otherwise difficult to measure. For instance, astronomers use parallax, which involves creating similar triangles, to calculate the distance to nearby stars. In physics, similar triangles can be used to calculate the height of physical objects from their shadows and the angle of the sun.
Geography and Surveying
Similar triangles are used in cartography to create scale maps. In surveying, they are used to determine distances and heights that can’t be measured directly.
Computer Science and Graphics
In computer graphics and gaming, similar triangles are often used to scale images and determine perspective, enabling objects to appear smaller the further they are from the viewer to create an illusion of depth.
Trigonometry and Calculus
The foundations of trigonometry are laid on the concept of similar triangles. For instance, trigonometric ratios remain constant for a given angle in similar triangles. In calculus, similar triangles are used in the derivation of derivative rules for trigonometric functions.
Medicine and Biology
In medical imaging, similar triangles can be used to calculate the sizes or distances of objects in an image. In biology, they are used in various models and analyses.
The ubiquitous nature of similar triangles in diverse fields stems from their fundamental properties and the relative ease of working with them mathematically.
Exercise
Example 1
Proving Similarity Using AA Criterion
Given two triangles ABC and DEF such that ∠A = ∠D and ∠B = ∠E. Prove that △ABC ~ △DEF.
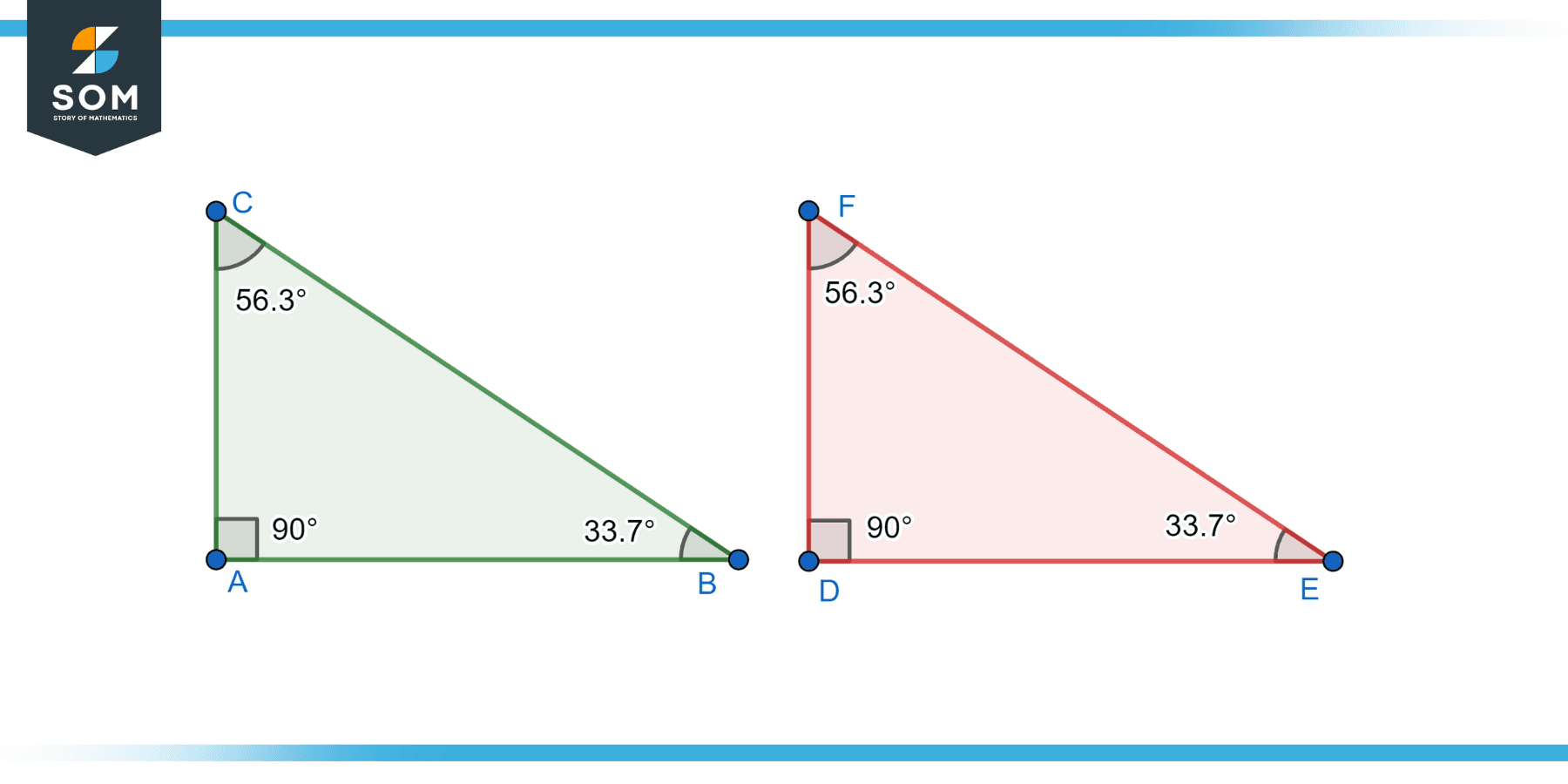
Figure-2.
Solution
Since ∠A = ∠D and ∠B = ∠E, by the AA (Angle-Angle) similarity postulate, △ABC ~ △DEF.
Example 2
Proving Similarity Using SAS Criterion
Given two triangles ABC and DEF, if AB/DE = BC/EF and ∠B = ∠E, prove that △ABC ~ △DEF.
Solution
Given the ratio of two sides and their included angles are equal, by the SAS (Side-Angle-Side) similarity postulate, △ABC ~ △DEF.
Example 3
Proving Similarity Using SSS Criterion
Given two triangles ABC and DEF, if AB/DE = BC/EF = AC/DF, prove that △ABC ~ △DEF.
Solution
Since the ratios of the lengths of corresponding sides of the triangles are equal, by the SSS (Side-Side-Side) similarity postulate, △ABC ~ △DEF.
Example 4
Finding Unknowns Using Similarity
In similar triangles △ABC and △DEF, if AB = 3 cm, BC = 4 cm, AC = 5 cm and EF = 12 cm. Find DE and DF.
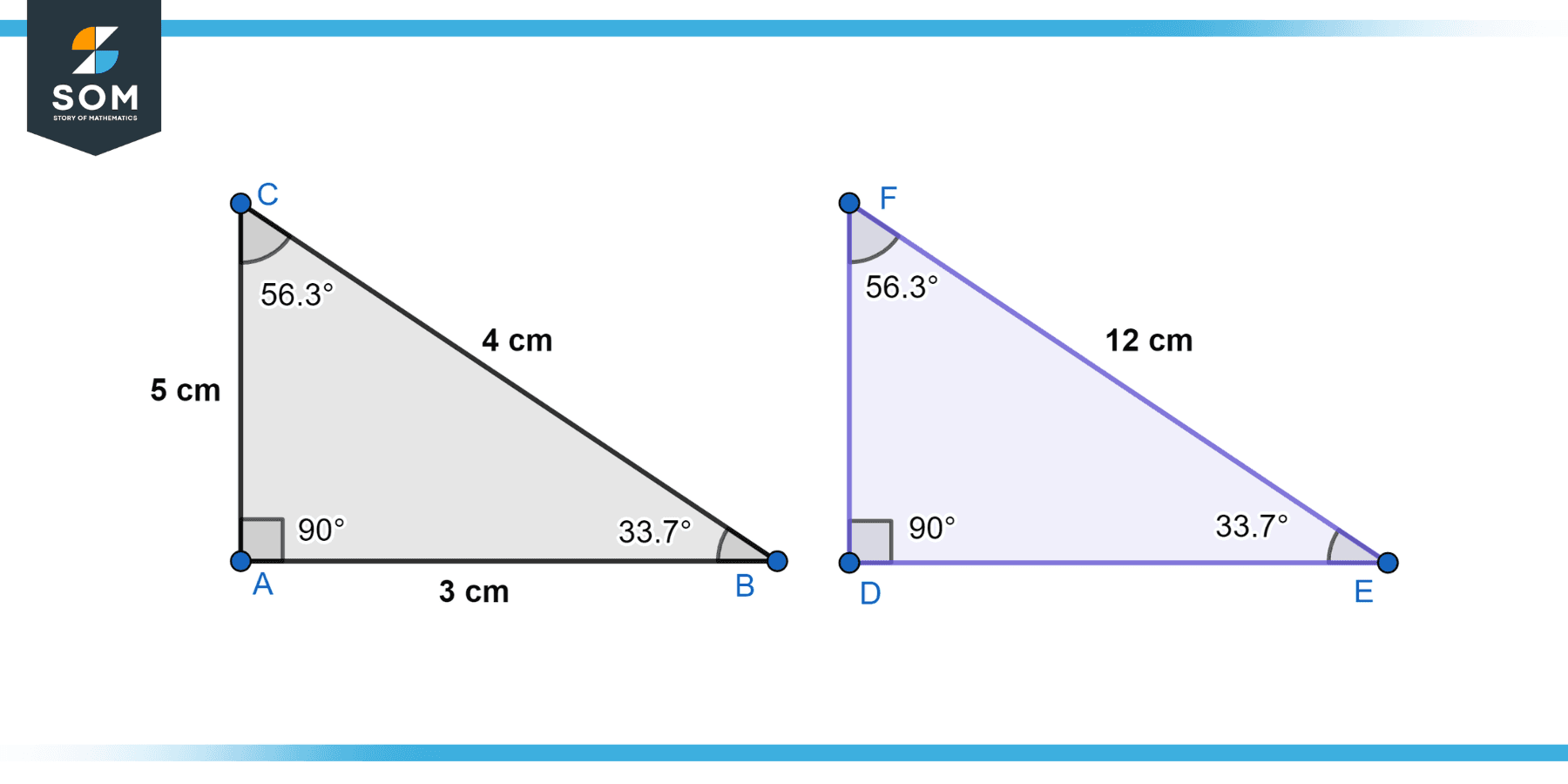
Figure-3.
Solution
Since △ABC ~ △DEF, we have DE/AB = EF/BC = DF/AC.
Therefore:
DE = (AB/BC) * EF
DE = (3/4) * 12
DE = 9 cm
Also:
DF = (AC/BC) * EF
DF = (5/4) * 12
DF = 15 cm
Example 5
Using Similar Triangles in Circles
In a circle with center O, chord AB is parallel to a tangent and the radius OC perpendicular to the tangent meets the chord at G. Prove that OG is half the length of OC.
Solution
Draw the radius OA to point A. Then △OGA and △OCA are similar (angle-angle criterion: ∠OGA = ∠OCA and ∠OAG = ∠OAC). Therefore, the ratio of corresponding sides is the same:
OG/OA = OA/OC
which simplifies to:
OG = $OA^2$/OC
But since OA = OC (both are radii of the circle), we have OG = OC/2, as required.
Example 6
Using Similarity in Right Triangles
In right triangle ABC, ∠ACB = 90°, AD is an altitude. Prove that △ABC ~ △BAD ~ △ACD.
Solution
Firstly, since ∠BAD = ∠B and ∠ABD = ∠ABC, by the AA criterion, △ABC ~ △BAD.
Secondly, since ∠ACD = ∠B and ∠ADC = ∠ABC, by the AA criterion, △ABC ~ △ACD.
Therefore, △ABC ~ △BAD ~ △ACD.
Example 7
Shadow Problems
A 6ft man is standing near a lamp post when he notices his shadow is 4ft long. At the same time, the lamp post’s shadow is 12ft long. How tall is the lamp post?
Solution
The triangles formed by the man and his shadow and the lamp post and its shadow are similar (by AA, as the angles of the sunlight are equal and each has a right angle). The ratio of the lamp post’s height (h) to the man’s height is the same as the ratio of the lamp post’s shadow to the man’s shadow. Therefore:
h/6 = 12/4
h = 18ft
Example 8
Using Similar Triangles in Trigonometry
In a right triangle ABC with ∠ACB = 90°, let ∠ABC = θ. If we take the side opposite ∠ABC as the opposite (O), side BC as the hypotenuse (H), and side AC as the adjacent (A), prove that sin(θ) = O/H and cos(θ) = A/H.
Solution
In right triangle ABC, the ratios O/H and A/H are invariant with the size of the triangle due to similarity (as all right triangles with angle θ are similar).
These ratios are defined as sin(θ) and cos(θ), respectively. Hence, the proof is a definition based on the properties of similar triangles.
All images were created with GeoGebra.
