JUMP TO TOPIC

Embrace the elegance of mathematics as we delve into the exciting world of absolute value limits. This article explores the concept of absolute value limits, highlighting the mathematical rules, important properties, and the powerful applications they hold.
Definition of Absolute Value Limits
In mathematics, the limit of a function as its argument or input tends towards a certain value is a fundamental concept in calculus. When we talk about the limit of an absolute value function, we are referring to this calculus concept but applied to a function involving absolute values.
The absolute value function is defined as |x| = x if x ≥ 0 and |x| = -x if x < 0. Consequently, when we consider the limit of an absolute value function, it’s important to recognize that the function behaves differently on either side of the point where the argument is zero. This can lead to situations where the right-hand limit and left-hand limit are not the same.
The limit of an absolute value function at a certain point is the value that the function approaches as the input (or argument) approaches that point.
For example, consider the function f(x) = |x – a|. As x approaches a from the right (x > a), f(x) approaches 0, and as x approaches a from the left (x < a), f(x) also approaches 0. Therefore, the limit of f(x) as x approaches a is 0.
However, consider the function g(x) = |x|. As x approaches 0 from the right, g(x) approaches 0, but as x approaches 0 from the left, g(x) also approaches 0. Therefore, the limit of g(x) as x approaches 0 is 0.
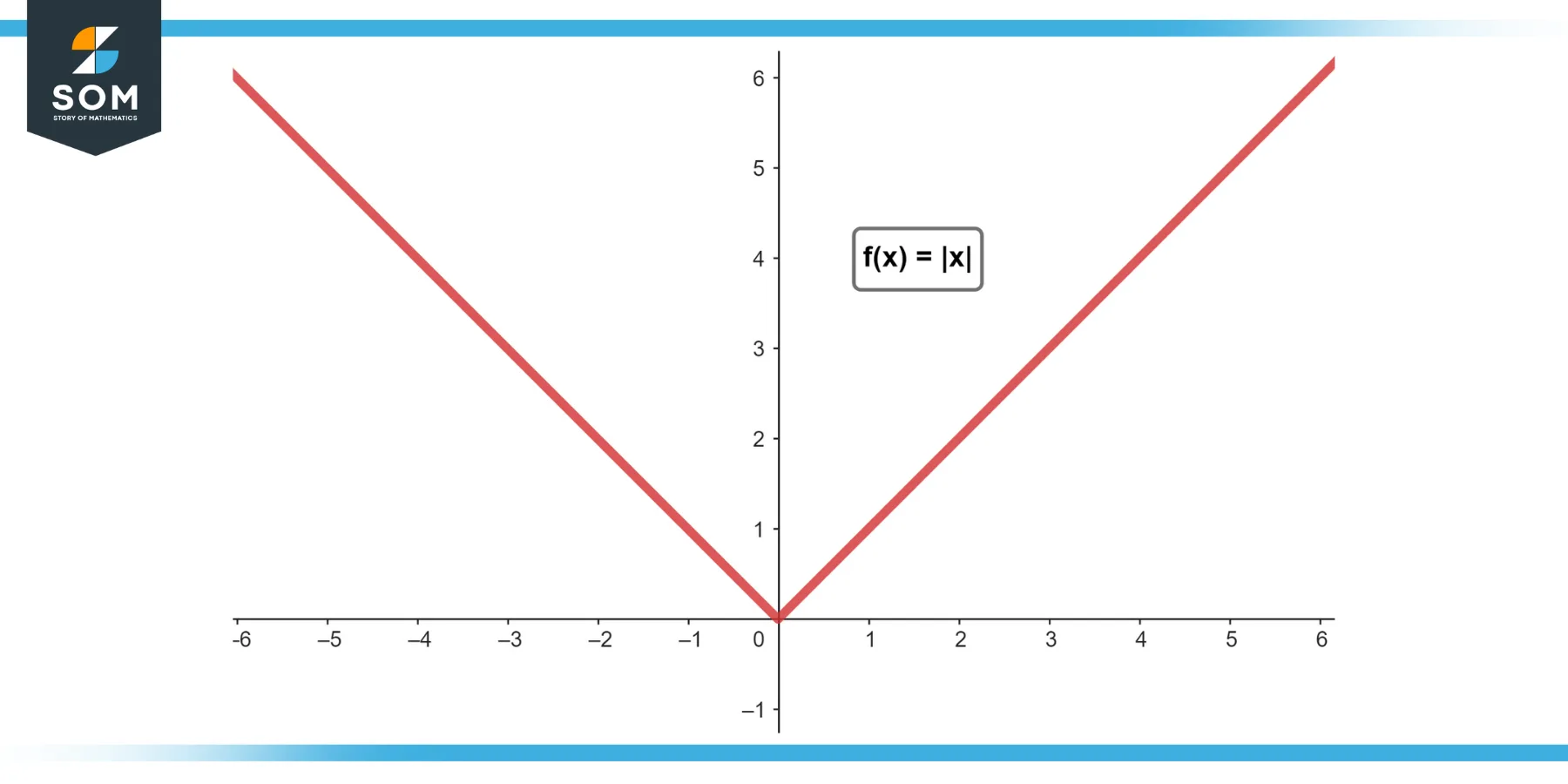
Figure-1.
Properties of Absolute Value Limits
The limit of an absolute value function shares many properties with limits in general. Here are some key properties of absolute value limits:
Limit of the Absolute Value of a Function
The absolute value limits of a function as x approaches a, can be written as:
lim (x→a) |f(x)|
This is equal to the absolute value limit of the function as x approaches a, if the limit exists.
Squeeze (Sandwich) Theorem
If a function is bounded by two other functions that approach the same limit as x approaches a, then the original function also approaches that limit. This theorem is often used when calculating the limits of absolute value functions.
Right-hand and Left-hand Limits
Because absolute value functions often have different behavior on either side of a certain point (most often where the function equals zero), it’s often necessary to calculate the right-hand limit (x approaching a from values greater than a) and the left-hand limit (x approaching a from values less than a) separately.
If these two one-sided limits are equal, then the limit of the function as x approaches a exists and is equal to this common value.
Limit of the Absolute Value of a Difference
If we have lim (x→a) |f(x) - g(x)| = 0, it implies that lim (x→a) f(x) = lim (x→a) g(x).
Absolute Value and Inequalities
If 0 < |x - a| < δ (where δ is a positive number), this means that x is in the interval (a - δ, a + δ), excluding the point x = a. This property is especially useful when proving limits.
Continuous at a Point
If a function f(x) is continuous at a point x = a, then |f(x)| is also continuous at x = a.
It’s important to note that, in practice, finding the limit of absolute value functions often involves breaking the function into piecewise-defined functions based on where the absolute value’s argument is positive or negative.
Exercise
Example 1
Find lim (x→2) |x - 2|.
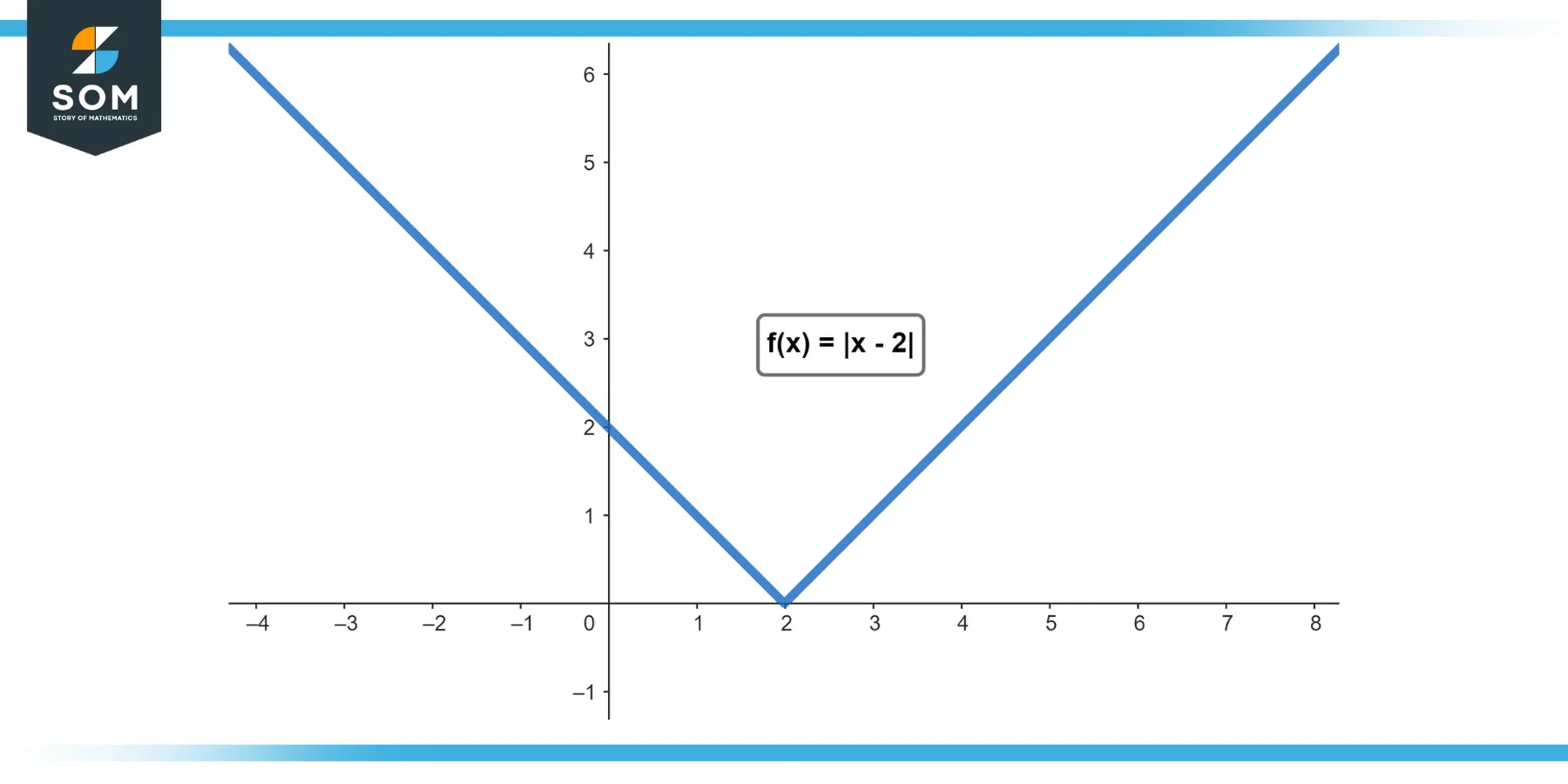
Figure-2.
Solution
Since |x - 2| equals 0 when x = 2, the limit as x approaches 2 is also 0.
Example 2
Find lim (x→3) |x - 3| / (x - 3).
Solution
This limit has different values from the right and from the left:
From the right (x > 3), |x - 3| = x - 3, so lim (x→3+) |x - 3| / (x - 3) = 1.
From the left (x < 3), |x - 3| = -(x - 3), so lim (x→3-) |x - 3| / (x - 3) = -1.
Since the left-hand limit does not equal the right-hand limit, the limit lim (x→3) |x - 3| / (x - 3) does not exist.
Example 3
Find lim (x→0) |x| / x.
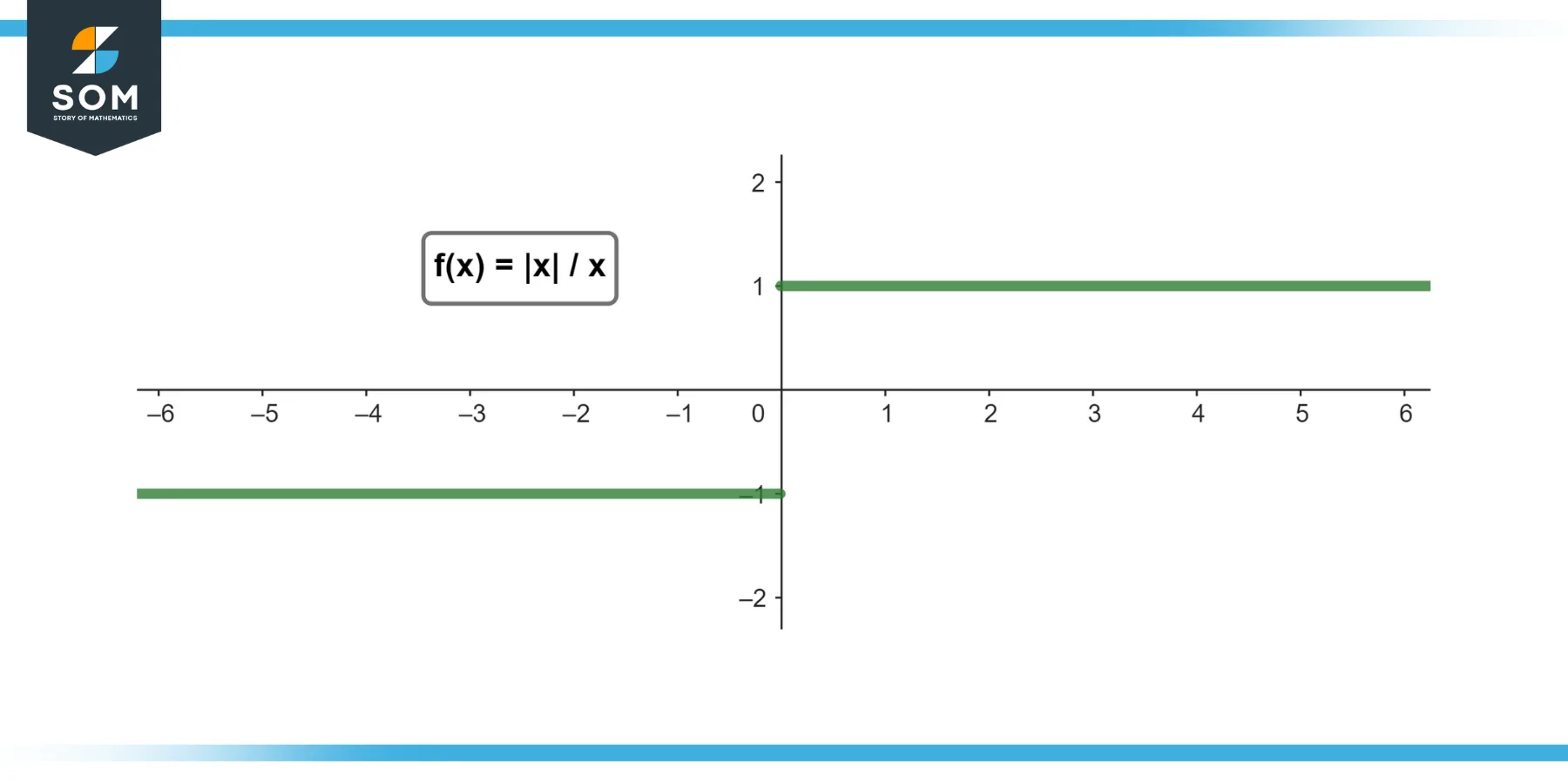
Figure-3.
Solution
From the right (x > 0), |x| = x, so lim (x→0+) |x| / x = 1.
From the left (x < 0), |x| = -x, so lim (x→0-) |x| / x = -1.
Since the left-hand limit does not equal the right-hand limit, the limit lim (x→0) |x| / x does not exist.
Example 4
Find lim (x→5) |x² - 25| / (x - 5).
Solution
We can simplify |x² - 25| to |x - 5||x + 5|. Therefore, the limit expression becomes |x + 5|.
So, lim (x→5) |x² - 25| / (x - 5) = |5 + 5| = 10.
Example 5
Find lim (x→-3) |2x + 6| / (2x + 6).
Solution
From the right (x > -3), |2x + 6| = 2x + 6, so lim (x→-3+) |2x + 6| / (2x + 6) = 1.
From the left (x < -3), |2x + 6| = -(2x + 6), so lim (x→-3-) |2x + 6| / (2x + 6) = -1.
Since the left-hand limit does not equal the right-hand limit, the limit lim (x→-3) |2x + 6| / (2x + 6) does not exist.
Example 6
Find lim (x→4) |x² - 16| / (x - 4).
Solution
We can simplify |x² - 16| to |x - 4||x + 4|. Therefore, the limit expression becomes |x + 4|.
So, lim (x→4) |x² - 16| / (x - 4) = |4 + 4| = 8.
Example 7
Find lim (x→0) |sin(x)| / x.
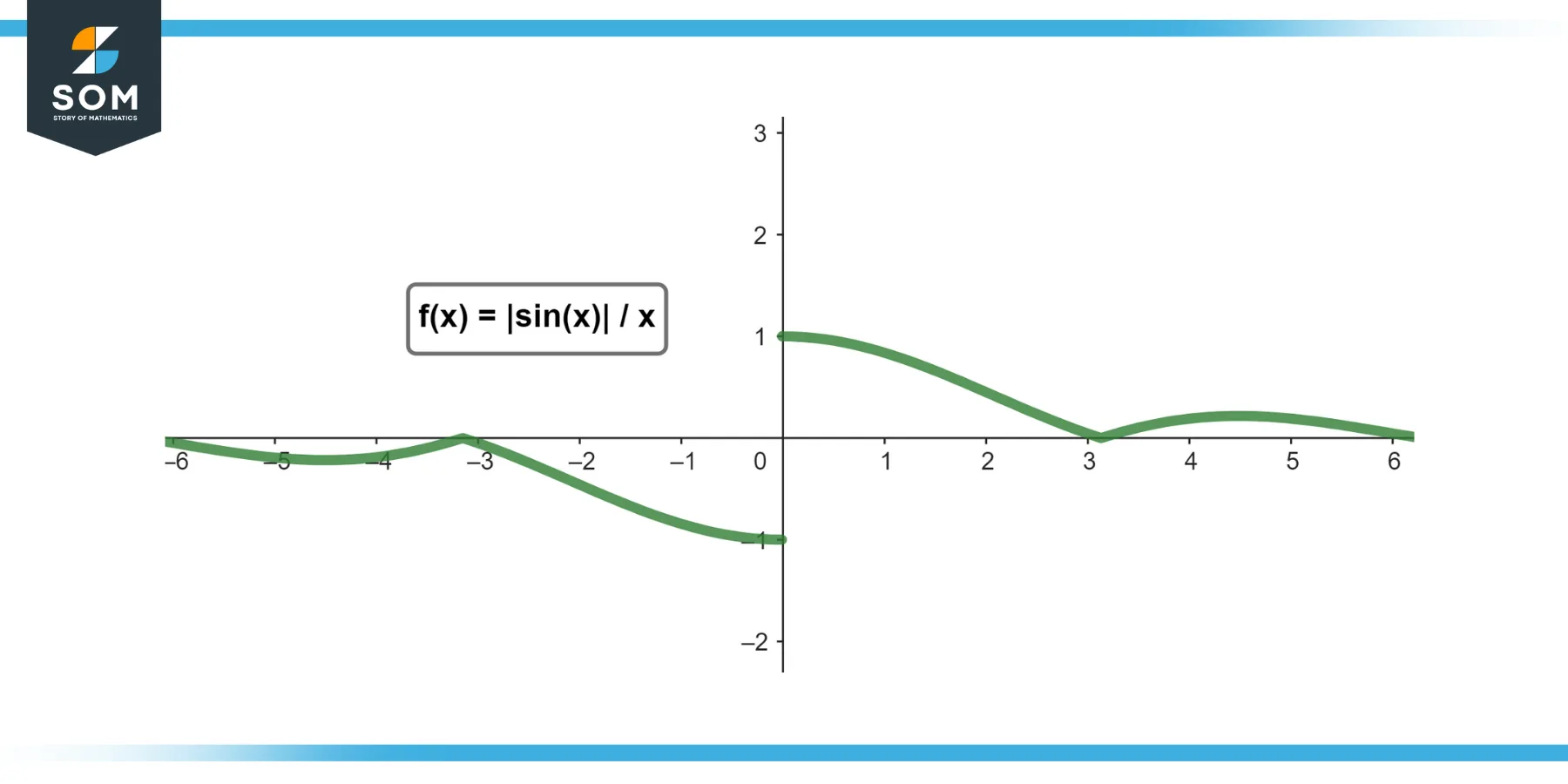
Figure-4.
Solution
From the right (x > 0), |sin(x)| = sin(x), so lim (x→0+) |sin(x)| / x = 1.
From the left (x < 0), |sin(x)| = -sin(x), so lim (x→0-) |sin(x)| / x = -1.
Since the left-hand limit does not equal the right-hand limit, the limit lim (x→0) |sin(x)| / x does not exist.
Example 8
Find lim (x→0) |x| / sin(x).
Solution
From the right (x > 0), |x| = x, so lim (x→0+) |x| / sin(x) = 1.
From the left (x < 0), |x| = -x, so lim (x→0-) |x| / sin(x) = -1.
Since the left-hand limit does not equal the right-hand limit, the limit lim (x→0) |x| / sin(x) does not exist.
Applications
The concept of absolute value limits not only holds importance within the realm of mathematical theory, but it also boasts applications across numerous scientific fields. Here are a few notable examples:
Physics
In physics, absolute value limits often come into play while evaluating certain physical quantities that cannot have a negative magnitude. For instance, determining the time at which a particle reaches a certain point, or studying properties of wave functions in quantum mechanics.
Engineering
In control systems engineering, the limit of absolute values is often used to analyze system stability. In electrical engineering, it’s used to find the maximum tolerable threshold levels for signals and currents.
Computer Science
In algorithm complexity analysis (Big O notation), limits of absolute values can help determine upper or lower bounds of algorithm performance. They’re also used in computer graphics to create certain visual effects and perform image processing.
Economics
Absolutely! In economics, absolute value limits are used to find equilibrium points, analyze trends, or determine the sensitivity of one economic variable to changes in another.
Biology
In mathematical biology, these limits can model population dynamics where the populations must remain non-negative.
Environmental Science
The concept of limits, including absolute value limits, is used in modeling pollutant dispersion, population growth, resource management, and more.
Statistics and Data Analysis
The absolute value limit is used when dealing with absolute differences, establishing thresholds, or defining metrics like Mean Absolute Error (MAE).
All images were created with GeoGebra.
