JUMP TO TOPIC

Today’s focus, the derivative of 2 to the x, is a cornerstone example that shines a light on the fundamental process of differentiation. We will illuminate the basic ideas of calculus by delving into the specifics of this situation, laying the groundwork for further mathematical investigations.
Embarking on a mathematical tour through the landscape of calculus, we invite readers to explore one of its fundamental ideas: the derivative, including the derivative of $2^{ x }$.
This article, designed for both the mathematically curious and those delving deeper into the world of calculus, provides an approachable yet thorough examination of this concept, ultimately demonstrating how the constant change encapsulated by the derivative powers our understanding of the mathematical world around us.
Understanding the Exponential Growth
The rapid and accelerating rise of a quantity over time is described by the fundamental mathematical and scientific notion of exponential growth. It occurs when a quantity continuously multiplies by a fixed growth rate, resulting in a dramatic rise that becomes more significant as time progresses.
This phenomenon can be observed in various fields, from biology and finance to technology and population dynamics. Understanding exponential growth is crucial as it has profound implications and applications in many aspects of our lives.
Understanding the exponential function is crucial for understanding exponential growth. A mathematical function with the formula f(x) = $a^{ x }$, where a is a constant greater than 1, and x is the independent variable, is known as an exponential function. When ‘x’ takes on larger values, the function grows at an accelerating rate, leading to exponential growth. The exponential function serves as a powerful tool for modeling and predicting various phenomena.
One of the most well-known examples of exponential expansion is the rise in population of living organisms. When conditions are right, populations can grow quickly, doubling in number within a predetermined period of time. Due to each person having children, who in turn help the population grow, there is a doubling effect.
As the population grows, there are more potential parents, which produces more children overall. This compounding effect characterizes exponential growth in biology.
Exponential growth also plays a vital role in technology and innovation. One of Intel’s co-founders, Gordon Moore, came up with Moore’s Law, which states that the number of transistors on a microchip doubles roughly every two years. This observation, which has held true for many years, has led to remarkable advancements in computing power and the miniaturization of electronic devices.
As a result, various fields, such as artificial intelligence and genomics, have experienced significant progress, benefiting from the exponential growth of technology that has revolutionized multiple industries.
Financial investments can also exhibit exponential growth. Compound interest, for instance, enables the growth of wealth over time. When interest is compounded, the accumulated interest is added back to the principal, resulting in a larger base for future growth. As the investment horizon extends, the compounding effect becomes more pronounced, and exponential growth can occur. For long-term financial planning and wealth growth, it is essential to comprehend the power of compound interest.
Despite its immense potential, exponential growth can also have negative consequences. In environmental science, exponential population growth can strain resources and lead to overconsumption, habitat destruction, and species extinction. Additionally, in the context of the COVID-19 pandemic, the exponential spread of the virus highlighted the importance of early intervention and mitigation strategies to prevent overwhelming healthcare systems.
Introduction to Derivatives
Calculus’s essential idea of derivatives, also known as rate of change, helps us comprehend how functions behave and how quickly they change. A derivative, at its foundation, assesses how a function reacts to infinitesimally minute changes in its input. It gives us vital details about a function’s slope at every particular position, allowing us to analyze its behavior, spot significant points, and make predictions. Below we present a generic rate of change example visualized.
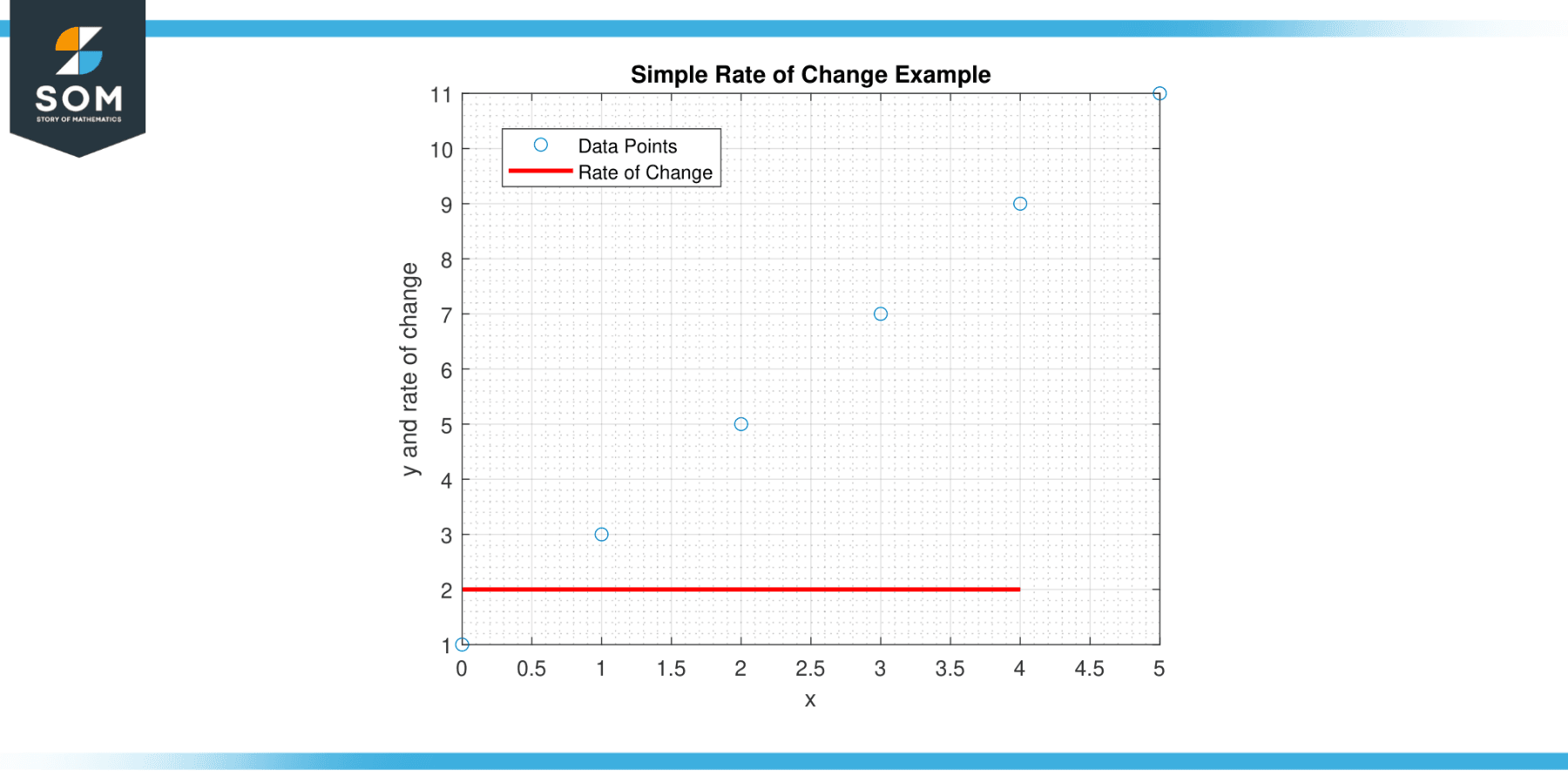
Figure-1.
The use of derivatives is widespread in many disciplines, including physics, engineering, economics, and biology. They form the basis for optimization, curve sketching, and understanding complex systems. By exploring derivatives, we gain powerful tools to unlock the secrets hidden within functions and delve deeper into the fascinating world of calculus.
Defining the Derivative of 2 to the x
The derivative of a function represents its rate of change or the slope of the tangent line at any given point. When it comes to the function f(x) = $2^{ x }$, the derivative is slightly more complex than polynomial functions like f(x) = $x^{ 2}$, due to the variable being the exponent.
Using the formula for the derivative of $a^{ x }$ (where ‘a’ is a constant), which is $a^{ x }$ * ln(a), we find that the derivative of $2^{ x }$ is $2^{ x }$ * ln(2). The function f(x) can be visualized in Figure-2 below.
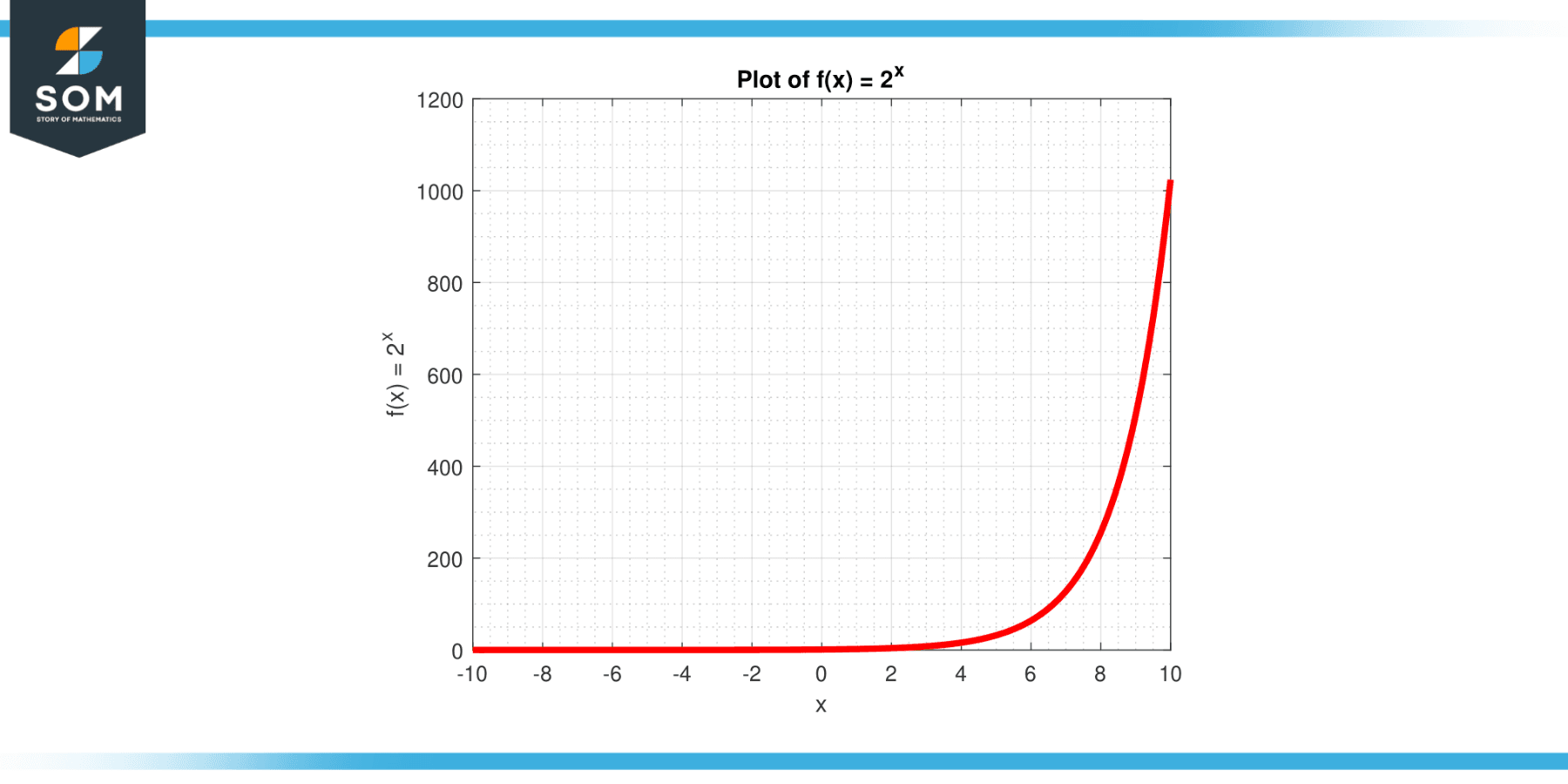
Figure-2.
So, for the function f(x) = $x^{ 2}$, its derivative, often denoted as f'(x) or df/dx, is $2^{ x }$ * ln(2). This means that at any point x, the rate of change of the function $2^{ x }$ is $2^{ x }$ * ln(2), where ln denotes the natural logarithm. The derivative of the function f(x) i.e., f'(x) can be visualized in Figure-3 below.
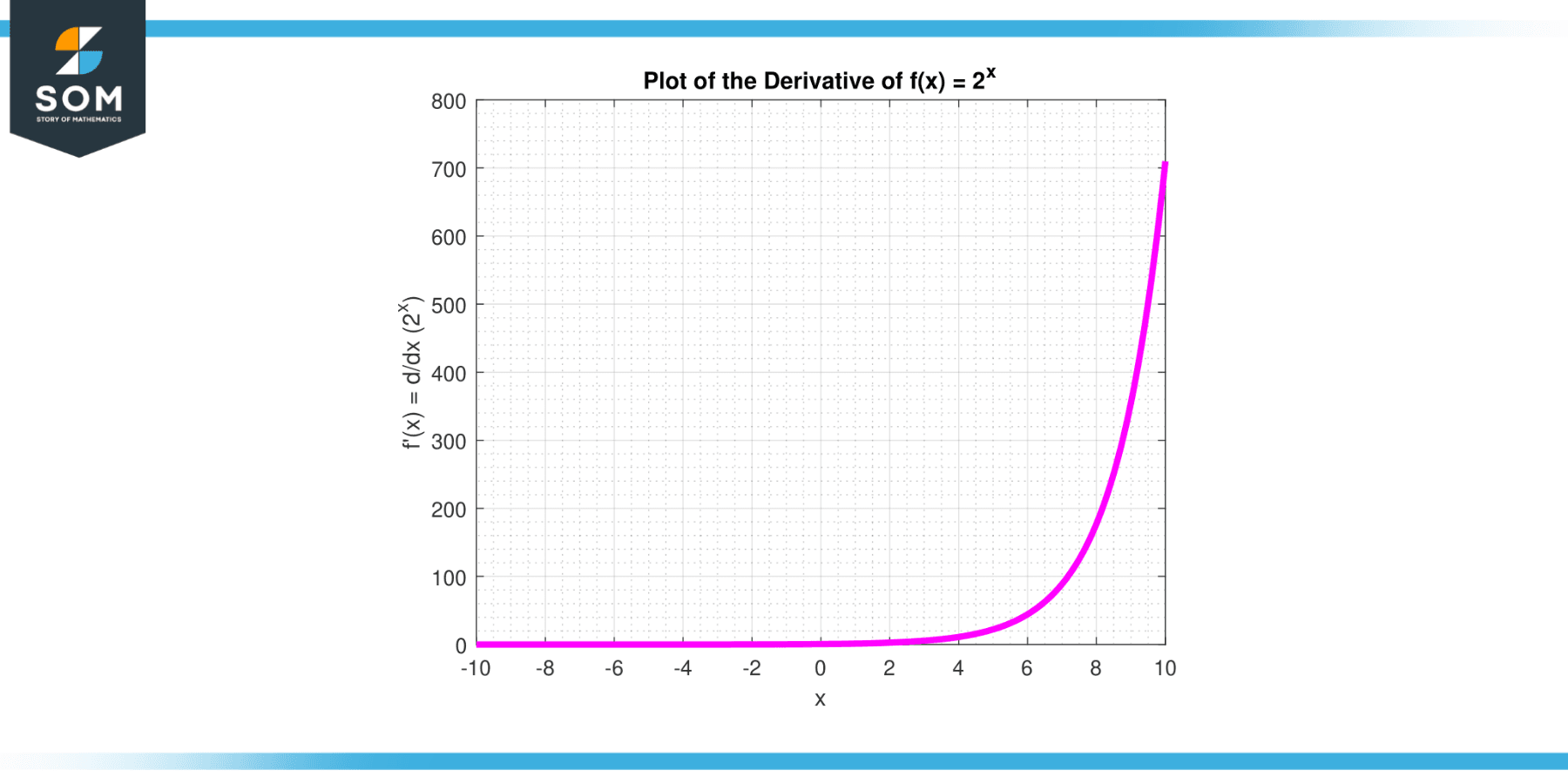
Figure-3.
The derivative provides valuable information about the behavior and characteristics of the function, such as identifying critical points, inflection points, and concavity. Understanding the derivative of $2^{ x }$ is fundamental in various fields, including physics, engineering, economics, and optimization problems, as it helps analyze the dynamics and optimization of quadratic functions.
Interpreting the Derivative of 2 to the x
The derivative of a function, as we’ve mentioned, is a measure of how that function changes as its input changes. Let’s interpret the derivative of the function f(x) = $2^{ x }$, which is f'(x) = $2^{ x }$ * ln(2).
This derivative tells us the rate at which the function $2^{ x }$ is changing at any given x. For example, at x = 0, the derivative $2^{ x }$* ln(2) equals;
$2^{ 0 }$ * ln(2) = ln(2) ≈ 0.693.
This means that at x = 0, the function $2^{ x }$ is increasing at a rate of 0.693 units per unit change in x.
Another way to visualize this is to imagine a tangent line touching the graph of the function at that point (x = 0, y = $2^{ 0 }$ = 1). The slope of that tangent line, which represents the instantaneous rate of change of the function at that point, is 0.693.
As x increases, the rate of change of the function also increases. This reflects the property of exponential growth: as the quantity grows, the rate at which it grows also speeds up. For instance, at x = 1, the derivative equals;
$2^{ 1}$ * ln(2) = 2 * ln(2) ≈ 1.386
Meaning that, at x = 1, the function $2^{ x }$ is increasing at almost twice the rate it was at x = 0.
Thus, interpreting the derivative of the function $2^{ x }$ provides insight into the nature of exponential growth and how small changes in the input x can lead to increasingly larger changes in the output as x gets larger. This concept is fundamental in areas of study where exponential growth is involved, such as in finance (compound interest), biology (population growth), physics (radioactive decay), and many others.
Properties
The derivative of an exponential function like $2^{ x }$, which is $2^{ x }$ * ln(2), exhibits several key properties that make it distinct from other types of functions. Here are some important properties:
Non-Negativity
The derivative of $2^{ x }$, i.e., $2^{ x }$ * ln(2), is always non-negative for any real number x. This means that the function $2^{ x }$ is always increasing or staying constant (it never decreases).
Continuity
The derivative is continuous for all real values of x. There are no abrupt changes, holes, or jumps in the derivative function. This is a reflection of the smooth, continuous growth of the exponential function itself.
Differentiability
The derivative of $2^{ x }$, $2^{ x }$ * ln(2), is differentiable at all points in its domain. This means that we can take the derivative of the derivative, leading to the second derivative, third derivative, and so on.
Exponential Growth
As x increases, the derivative $2^{ x }$ * ln(2) increases exponentially. This means that the rate of change of the function $2^{ x }$ accelerates as x gets larger. This is the characteristic feature of exponential growth: as the quantity grows, the rate at which it grows speeds up.
Dependence on the Base
The derivative of $2^{ x }$ depends on the base ‘2’. If we change the base, the derivative changes accordingly. The base appears in the derivative as a factor of ln(2), making the derivative of $a^{ x }$ equal to $a^{ x }$ * ln(a) for any base ‘a’. This shows the deep connection between exponential functions and logarithms in calculus.
These properties underscore the unique behavior of exponential functions and their derivatives. They help us understand why exponential functions model certain types of growth and change so effectively, and they offer insights into the mathematical structure of the exponential functions themselves.
Applications and Significance
The derivatives of exponential functions, such as the derivative of $2^{ x }$, have widespread applications and profound significance in a variety of fields:
Physics
One of the most important applications of exponential derivatives is in the field of physics, specifically in the study of motion, force, and energy. For instance, radioactive decay and population growth can be modeled by exponential functions, and their rates of change are described by their derivatives.
Biology
In biology, derivatives of exponential functions are used to model population growth, especially for species that reproduce exponentially. They’re also used in modeling the spread of diseases or the growth of cells and bacteria.
Finance and Economics
When it comes to compound interest or the growth of investments, exponential growth is a frequent occurrence in the world of finance. A useful piece of information regarding a return rate or an investment’s susceptibility to changes in market conditions can be found in the derivative of these functions.
Computer Science
In computer science, particularly in the area of algorithms and data structures, the exponential function and its derivative are very important. The analysis of algorithm complexity often involves understanding the behavior of exponential functions.
Engineering
In engineering fields, such as electrical engineering, the behavior of circuits, especially those involving capacitors and inductors, can be modeled using exponential functions, making their derivatives critical for understanding and predicting circuit behaviors.
In a nutshell, the derivative of the function 2^x and other exponential functions offer fundamental insights into the world around us. They help us quantify and predict change, offering a powerful tool for a wide range of disciplines. The deep-seated relationship between exponential functions and their derivatives underscores the interconnected nature of mathematical concepts and their profound impact across diverse fields of study.
Exercise
Example 1
Given the function f(x) = $2^{ x }$, find the derivative at x = 2.
Solution
f´(x) = $2^{ x }$ * ln(2)
Substituting x = 2, we get:
f´(2) = $2^{ 2 }$ * ln(2)
f´(2) = 4 * ln(2)
f´(2) ≈ 2.77259
Example 2
Consider the function g(x) = 3 * $2^{ x }$. Find the derivative of g(x).
Solution
Using the constant multiple rules, we can write g(x) as g(x) = 3 * f(x), where f(x) = $2^{ x }$. Taking the derivative:
g´(x) = 3 * f´(x)
g´(x) = 3 * ($2^{ x }$ * ln(2))
The function g(x) and its derivative can be visualized in Figure-4.
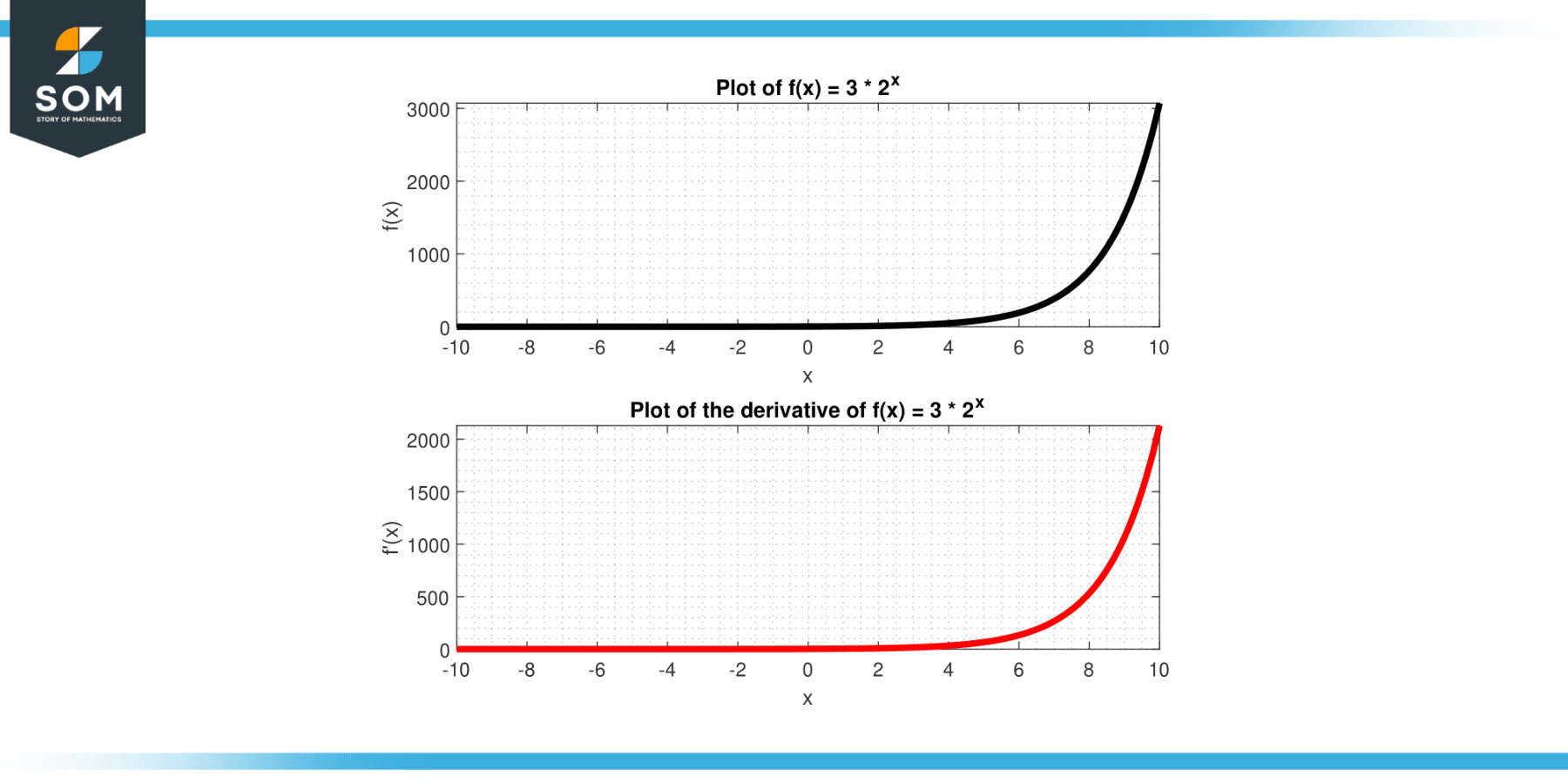
Figure-4.
Example 3
Let’s examine the function h(x) = ($2^{ x }$) / x. Determine the derivative of h(x).
Solution
Applying the quotient rule, we have:
h´(x) = [(x * f´(x)) – (f(x) * 1)] / (x^2)
h´(x) = [(x * ($2^{ x }$ * ln(2))) – (($2^{ x }$) * 1)] / ($2^{ x }$)
Example 4
Compute the slope of the tangent line to the graph of $y = 2^{ x }$ at the point where x=2:
Solution
The slope of the tangent line to the graph at a given point is given by the derivative evaluated at that point. So, we compute the derivative $2^{ x }$ * ln(2) at x=2 to get:
$2^{ 2 }$ * ln(2) = 4*ln(2)
Consequently, the slope of the tangent line to the graph at x=2 is 2.77259.
All figures are generated using MATLAB.
