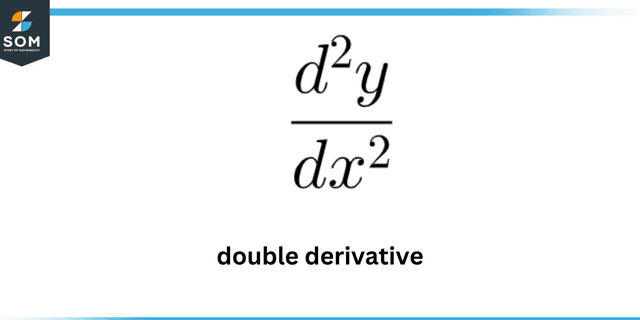JUMP TO TOPIC
The aim of this question is to introduce the local maxima and minima of a curve.
Local maxima are defined as the point where the absolute value of the function is maximum. Local minima are defined as the point where the absolute value of the function is minimum.
Maxima
Minima
To evaluate these values, we need to find the first and second derivatives of the given function. However, to evaluate the curvature maxima we need to follow a different procedure that is elaborated in detail in the following section.
Expert Answer
Given that:
\[ y \ = \ 9 \ ln( x ) \]
Taking derivative:
\[ y^{ ‘ } \ = \ 9 \ \dfrac{ d }{ dx } \bigg ( ln( x ) \bigg ) \]
\[ y^{ ‘ } \ = \ 9 \ \bigg ( \dfrac{ 1 }{ x } \bigg ) \]
\[ y^{ ‘ } \ = \ \dfrac{ 9 }{ x } \]
Taking derivative:
\[ y^{ ” } \ = \ 9 \ \dfrac{ d }{ dx } \bigg ( \dfrac{ 1 }{ x } \bigg ) \]
\[ y^{ ” } \ = \ 9 \ \bigg ( \dfrac{ – 1 }{ x^2 } \bigg ) \]
\[ y^{ ” } \ = \ – \dfrac{ 9 }{ x^2 } \]
Calculating K(x) using the following formula:
\[ k(x) \ =\ \dfrac{ | y^{ ” } | }{ ( 1 \ + \ ( y^{ ‘ } )^2 )^{ \frac{ 3 }{ 2 } } } \]
Substituting values:
\[ k(x) \ =\ \dfrac{ \bigg | – \dfrac{ 9 }{ x^2 } \bigg | }{ \Bigg ( 1 \ + \ \bigg ( \dfrac{ 9 }{ x } \bigg )^2 \Bigg )^{ \frac{ 3 }{ 2 } } } \]
\[ k(x) \ =\ \dfrac{ 9 }{ x^2 } \times \dfrac{ ( x^2 )^\frac{ 3 }{ 2 } }{ ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } } \]
\[ k(x) \ =\ \dfrac{ 9 }{ x^2 } \times \dfrac{ x^3 }{ ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } } \]
\[ k(x) \ =\ \dfrac{ 9 x }{ ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } } \]
Taking derivative:
\[ k^{ ‘ }(x) \ =\ \dfrac{ d }{ dx } \Bigg ( \dfrac{ 9 x }{ ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } } \Bigg ) \]
\[ k^{ ‘ }(x) \ =\ \dfrac{ \dfrac{ d }{ dx } \Bigg ( 9 x \Bigg ) ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } \ – \ ( 9 x ) \dfrac{ d }{ dx } \Bigg ( ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } \Bigg ) }{ \Bigg ( ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } \Bigg )^{ 2 } } \]
\[ k^{ ‘ }(x) \ =\ \dfrac{ 9 ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } \ – \ ( 9 x ) \Bigg ( \frac{ 3 }{ 2 } ( x^2 \ + \ 81 )^{ \frac{ 1 }{ 2 } } ( 2 x ) \Bigg ) }{ ( x^2 \ + \ 81 )^{ 3 } } \]
\[ k^{ ‘ }(x) \ =\ 9 \dfrac{ ( x^2 \ + \ 81 )^{ \frac{ 3 }{ 2 } } \ – \ 3 x^2 \sqrt{ x^2 \ + \ 81 } }{ ( x^2 \ + \ 81 )^{ 3 } } \]
\[ k^{ ‘ }(x) \ =\ \dfrac{ 9 ( – 2 x^2 \ + \ 81 ) }{ ( x^2 \ + \ 81 )^{ \frac{ 5 }{ 2 } } } \]
To proceed further, we need to solve the above equation for $ k^{ ‘ }(x) = 0 $:
\[ \dfrac{ 9 ( – 2 x^2 \ + \ 81 ) }{ ( x^2 \ + \ 81 )^{ \frac{ 5 }{ 2 } } } \ =\ 0 \]
We get the following roots:
\[ x \ = \ \pm \dfrac{ 9 \sqrt{ 2 } }{ 2 } \]
We may conclude that we will have curvature maxima at the following point:
\[ x \ = \ \dfrac{ 9 \sqrt{ 2 } }{ 2 } \]
Calculating the value of y at this value:
\[ y \ = \ 9 \ ln \bigg ( \dfrac{ 9 \sqrt{ 2 } }{ 2 } \bigg ) \]
So the point of maximum curvature is the following:
\[ (x, y) \ = \ \Bigg ( \dfrac{ 9 \sqrt{ 2 } }{ 2 } , \ 9 \ ln \bigg ( \dfrac{ 9 \sqrt{ 2 } }{ 2 } \bigg ) \Bigg ) \]
Numerical Result
\[ (x, y) \ = \ \Bigg ( \dfrac{ 9 \sqrt{ 2 } }{ 2 } , \ 9 \ ln \bigg ( \dfrac{ 9 \sqrt{ 2 } }{ 2 } \bigg ) \Bigg ) \]
Example
In the above question, what will happen if x approaches infinity?
From the above solution:
\[ k^{ ‘ }(x) \ =\ \dfrac{ 9 ( – 2 x^2 \ + \ 81 ) }{ ( x^2 \ + \ 81 )^{ \frac{ 5 }{ 2 } } } \]
Applying limits:
\[ \begin{array}{c} Lim \\ x \rightarrow \infty \end{array} k^{ ‘ }(x) \ =\ \begin{array}{c} Lim \\ x \rightarrow \infty \end{array} \dfrac{ 9 ( – 2 x^2 \ + \ 81 ) }{ ( x^2 \ + \ 81 )^{ \frac{ 5 }{ 2 } } } \]
Since the degree of the denominator is higher than the numerator:
\[ \begin{array}{c} Lim \\ x \rightarrow \infty \end{array} k^{ ‘ }(x) \ =\ 0 \]