JUMP TO TOPIC
 The box method is considered one of the easiest and most fun ways of factoring trinomials because it uses a box to factor a quadratic polynomial completely. You have to place the first and last terms of the quadratic expression in the box and perform the indicated steps to obtain the factors.
The box method is considered one of the easiest and most fun ways of factoring trinomials because it uses a box to factor a quadratic polynomial completely. You have to place the first and last terms of the quadratic expression in the box and perform the indicated steps to obtain the factors.
In this guide, we will discuss the steps in performing the box method to factor quadratic trinomials completely. We will also provide examples with detailed solutions to show how to use the box method.
What Is Box Method?
The box method is a technique used in factoring quadratic trinomials consisting of a box where you need to put the first and last terms of the quadratic polynomial.
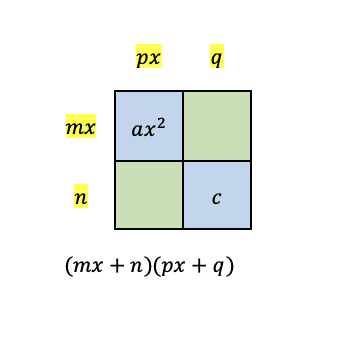
Figure 1 shows what the box method looks like when you factor the polynomial $ax^2+bx+c$. You need to place the first and last terms in the diagonal, then you need to follow the indicated steps to solve the terms that need to be placed in the green cells. Using these cells, you will derive the terms $mx$, $px$, $n$, and $q$. Then the quadratic trinomial can be expressed as factors of $mx+n$ and $px+q$.
How To Use Box Method
Let’s learn the steps in using the box method in this section to learn how to obtain the missing terms and parts of the box.
We can use the box method by performing the following steps. We consider the standard form of a quadratic polynomial:
$$ax^2+bx+c.$$
Step 1

Step 2
Take the product of the coefficients of the first and last terms of the trinomial. Then look for two terms $u$ and $v$ such that the product of $u$ and $v$ is equal to the product of the coefficients of the first and last term, and the sum of $ux$ and $vx$ is the middle term. That is,
$$uv=ac$$
and
$$ux+vx=bx.$$
Step 3
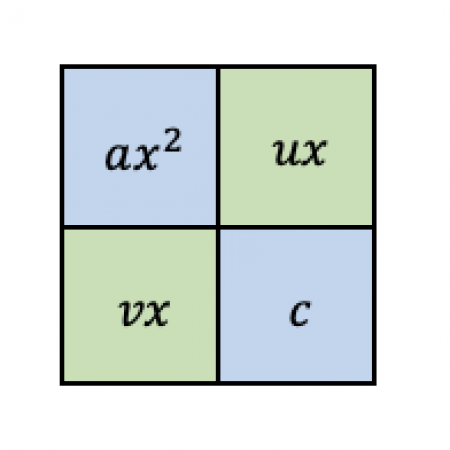
Step 4
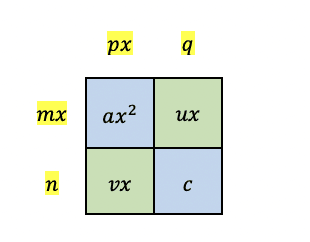
In Figure 4, the highlighted terms are the greatest common factor for each pairing.
\begin{align*}
mx&=gcf(ax^2,ux)\\
n&=gcf(vx,c)\\
px&=gcf(ax^2,vx)\\
q&=gcf(ux,c)
\end{align*}
It is important to note the signs of the terms. For each greatest common factor, take the sign of the closest term. Those are the signs of the terms in the first column and first row.
Step 5
Example 1
Use the box method to find the factors of $3x^2+10x+8$.
- Step 1. We place the first and last terms, $3x^2$ and $8$, in the diagonals in the box.

- Step 2. We take the product of the coefficients of the first and last terms, \begin{align*} 3\times8=24. \end{align*}
- Step 3. Since we now have the two numbers $4$ and $6$, we place the terms $4x$ and $6x$ on the other diagonal.
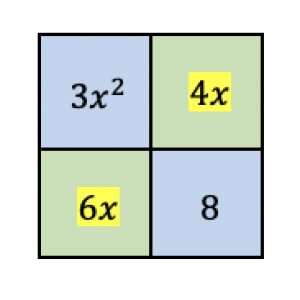
- Step 4. We now solve for the greatest common factor for each row and column.
The terms in the first column are $3x^2$ and $6x$. The greatest common factor of $3x^2$ and $6x$ is $3x$ because
\begin{align*}
gcf(3,6)=3
\end{align*}
and
\begin{align*}
gcf(x,x^2 )&=x\\
\Rightarrow gcf(3x^2,6x)&=3x.
\end{align*}
Then we place $3x$ at the top of the column.
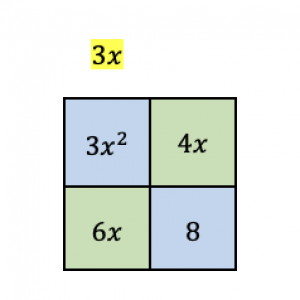
Next, the terms in the second column are $4x$ and $8$ and their greatest common factor is $4$. We write this at the top of the second column.
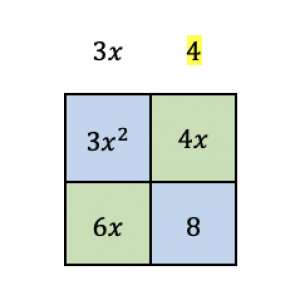
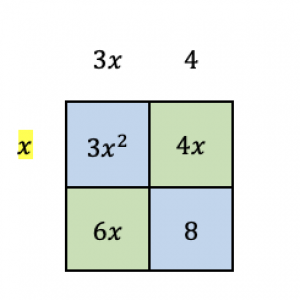
Finally, we find the greatest common factor of $6x$ and $8$, the terms in the bottom row of the box.
\begin{align*}
gcf (6x,8)=2
\end{align*}
Then affix it at the left of the last row.
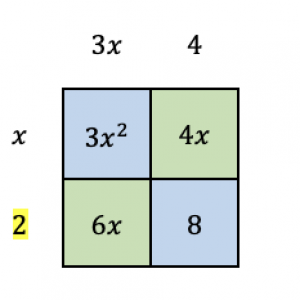
- Step 5. Since we have solved all the greatest common factors for each pair of terms in the rows and columns of the box, we take the sum of the terms at the top of the box
\begin{align*}
3x+4
\end{align*}
and the sum of the terms at the left of the box
\begin{align*}
x+2.
\end{align*}
Thus, the factoring of the polynomial is given by
\begin{align*}
3x^2+10x+8=(3x+4)(x+2).
\end{align*}
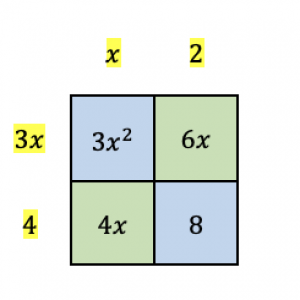
We also mentioned that the placement of the terms in Step 3 will not affect the factors that we will get, so let’s try to interchange the position of $4x$ and $6x$.
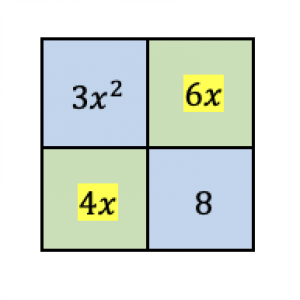
Then,
\begin{align*}
gcf(3x^2,4x)&=x\\
gcf(6x,8)&=2\\
gcf(3x^2,6x)&=3x\\
gcf(4x,8)&=4.
\end{align*}
Notice that the pairings for the columns and rows did not change, so the greatest common factors we obtained remained the same. Placing these common factors outside the box, we have:
Example 2
Factor the expression $2x^2-9x-5$ using the box method.
- Place the $2x^2$ and $-5$ in the diagonals of the box.
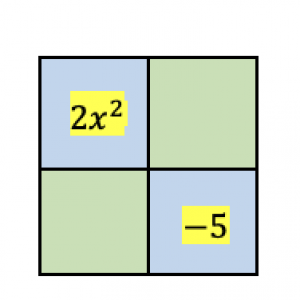
- We look for factors of $2\times-5=-10$ that will give as a sum of $-9$, the coefficient of the middle term. The factors of $10$ are $1$ and $10$, and $2$ and $5$. Since $-10$ is a negative number, then its factors are of opposing signs. Among these pairs, $-10$ and $1$ have a sum of $-9$.
- We place the terms $x$ and $-10x$ in the box.

- We solve for the greatest common factor of each pair of terms.
\begin{align*}
gcf(2x^2,10x)=2x
\end{align*}
Note that since we have negative signs in the box, we take the signs of the closest terms for the factors. Since the $2x^2$ is the closest term at the first column and first row, and its sign is positive, then its greatest common factor is also positive.
\begin{align*}
gcf(2x^2,-10x)&=2x\\
gcf(2x^2,x)&=x.
\end{align*}
Similarly, since $x$ is positive and is the closest term in the second row of the box, then
\begin{align*}
gcf(x,-5)=1.
\end{align*}
For the last row, $-10x$ is the closest term on the left side of the box and has a negative sign, then its greatest common factor is also negative.
\begin{align*}
gcf(-10x,-5)=-5.
\end{align*}
Then we place these terms in their respective positions outside the box.
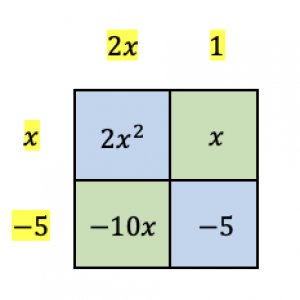
Conclusion
In this guide, we discussed the steps on how to use the box method in factoring quadratic trinomials. We also have applied the steps in the examples where we explored trinomials with positive and negative coefficients.
- The box method is one of the techniques used in factoring trinomials that uses a box where we place the first and last terms of the polynomial in the diagonal cells of the box.
- The factors obtained using the box method are derived from the greatest common factors of the terms inside the box.
- You can place the terms in any cells on the left diagonal. Either way, you will get the same factors after performing the proceeding steps of the box method.
- For trinomials with coefficients of different signs, you must take the sign of the term closest as the sign of the greatest common factor.
The box method is an entertaining way of solving factors of a quadratic trinomial because it goes away from the traditional ways of solving mathematical problems. It helps students remember how to solve these types of problems, and although there are many other ways to solve quadratic equations, this one helps students remember what they learned while still being exciting.
