What Is -b/2a and Why Is It Important in Math?

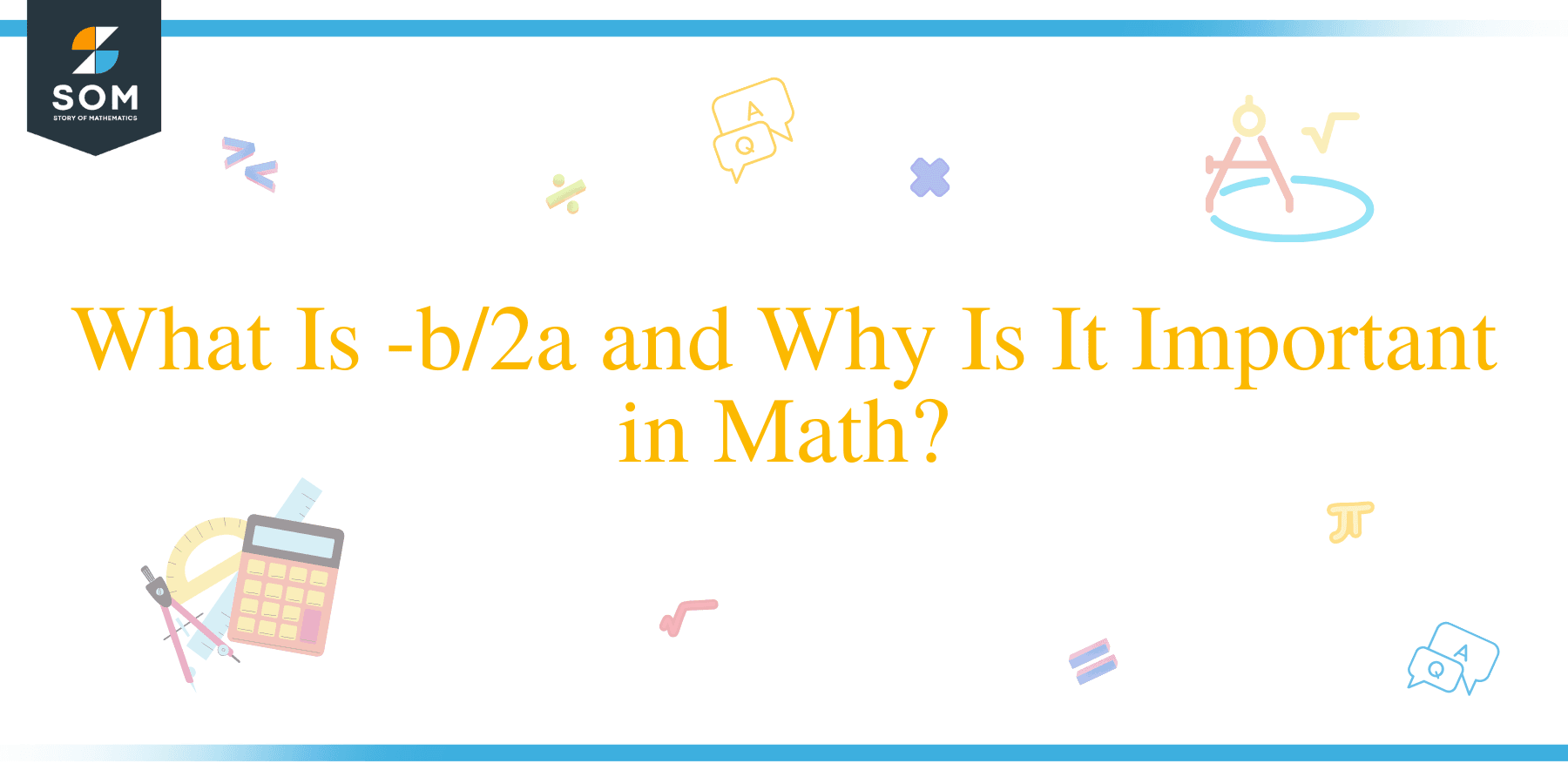The expression -b/2a is based on the constants of a quadratic equation and allows us to identify the vertex of a parabola. If you’re looking for an article that helps you understand the –b/2a and the vertex form, you just reached the right one. This discussion covers everything you need to know about this expression – from finding its value using the quadratic equation to applying it for the vertex form.

What Is -b/2a?

In a quadratic equation, $-b/2a$ represents the $x$-coordinate of the quadratic function’s vertex — this means that $-b/2a$ is the value of $x$ where the quadratic function or equation is at its minimum or maximum. When written in standard form, $a$ and $b$ represent the first two coefficients of the quadratic equation, $ax^2 +bx+c =0$.

Why Is -b/2a Important in Quadratic Equation?

It is important because through the value of $-b/2a$, formally called the vertex formula (or vertex form), it is now much easier to identify the vertex of the quadratic function without graphing its curve first. The variable, $D$, is a crucial element for the vertex’s $y$-coordinate. This represents the discriminant of the quadratic equation: $D = b^2 – 4ac$. In fact, $-b/2a$ is the solution of the quadratic equation when its discriminant is equal to zero.

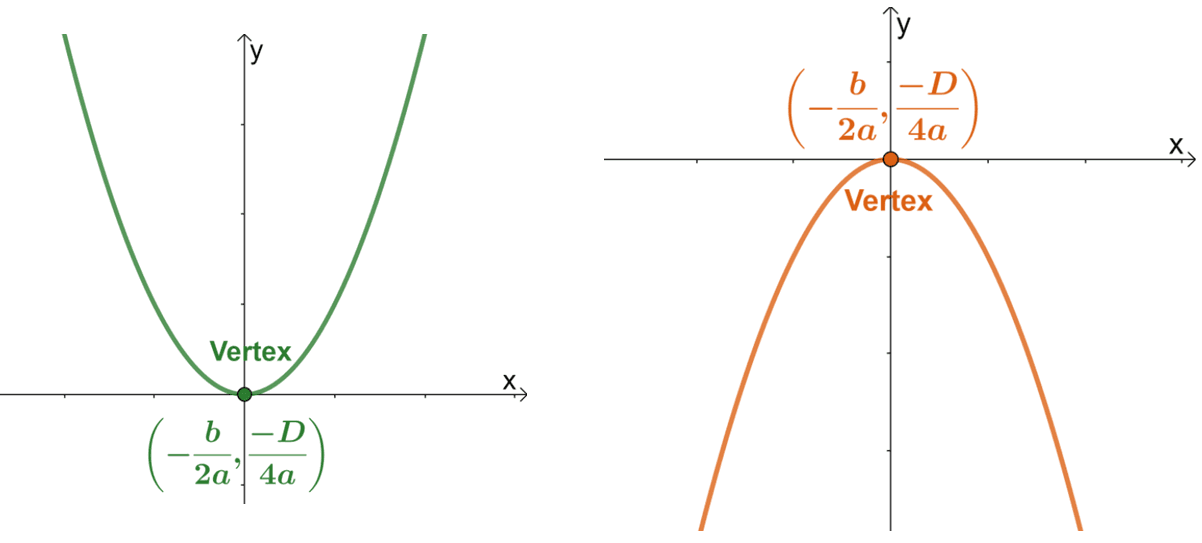
Why Is -b/2a Important in Vertex Formula?

It is important because the vertex form of the quadratic equation and function is an essential formula used to calculate the minimum or maximum point of the function given its quadratic equation’s coefficients.

\begin{aligned}&\textbf{Vertex } \textbf{ Formula}\\\\(h, k)&= \left(-\dfrac{b}{2a}, \dfrac{-D}{4a}\right)\\&= \left(-\dfrac{b}{2a}, \dfrac{4ac – b^2}{4a}\right)\end{aligned}

Similar to the quadratic formula, the values of $a$, $b$, and $c$ will be equal to the coefficients of the given quadratic equation or function’s standard form, $ax^2 + bx +c =0$. In addition, $h$ and $k$ represent the $x$ and $y$ coordinates of the quadratic function’s vertex.

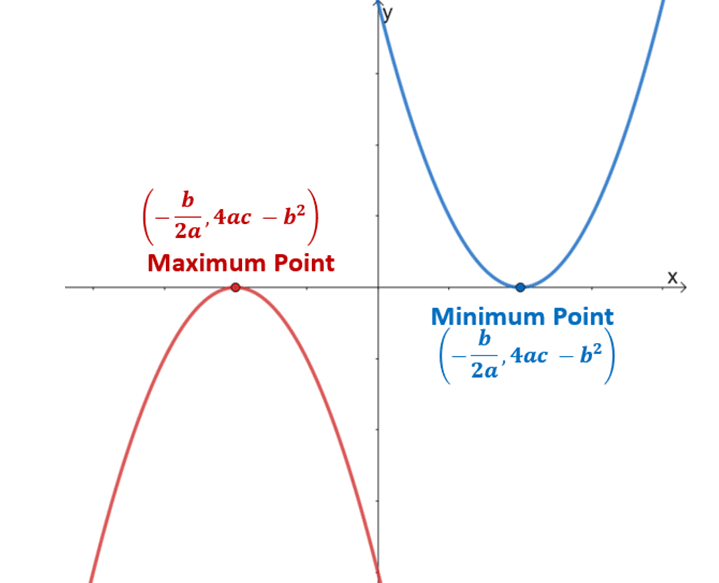
This means that by inspecting the coefficients of the quadratic function, it is now straightforward to determine its vertex and consequently, the minimum or maximum point. Take a look at these examples to better appreciate the vertex form as well.

These three examples highlight the importance of the vertex form. Without graphing the function, it is now easier to simply find the vertex of the function’s parabola. In addition, without using advanced math techniques, it is now possible to determine the quadratic function or the equation’s maximum and minimum point.

Are you curious about how the vertex form is derived? Then the next section is for you. Don’t worry, if you want to try out some examples and learn how to apply the formula, skip over the next section and jump right into the $-b/2a$ and the vertex formula’s application.

How To Prove the Vertex Formula and -b/2a?

When deriving the vertex form, factor the standard form of quadratic equations, $ax^2+ bx+ c = 0$, and apply the completing the square method to prove the vertex formula. This is to rewrite the quadratic equation or quadratic function in its vertex form. Follow through the steps below to understand how $y =ax^2 + bx + c$ is rewritten to its vertex form.

\begin{aligned}ax^2 + bx +c &= y\\ax^2 + bx + \_\_\_&= y-c\\y-c &= ax^2 + bx + \_\_\_\end{aligned}

Now factor out $a$ on the right-hand side of the equation. To rewrite the right-hand side of the equation as a perfect square trinomial, add both sides by $a\left(\dfrac{b}{2a}\right)^2$.

\begin{aligned}y -c + a (\_\_\_) &= a\left(x^2 + \dfrac{b}{a}x + \_\_\_\right)\\y- c +a\left(\dfrac{b}{2a}\right)^2 &= a\left[x^2 + \dfrac{b}{a}x +\left(\dfrac{b}{2a}\right)^2\right]\\y – c + \dfrac{b^2}{4a}&= a\left(x + \dfrac{b}{2a}\right)^2\end{aligned}

Recall that the vertex form of a quadratic function is $y = a(x – h)^2 + k$, where $(h, k)$ represents the vertex of the function.

\begin{aligned}y + \dfrac{b^2 – 4ac}{4a}&= a\left(x + \dfrac{b}{2a}\right)^2\\y – \dfrac{4ac – b^2}{4a}&= a\left(x + \dfrac{b}{2a}\right)^2 + \dfrac{4ac – b^2}{4a}\\\textbf{Vertex } &:\left(-\dfrac{b}{2a}, \dfrac{4ac – b^2}{4a}\right)\end{aligned}

This confirms that the vertex of any quadratic function can be expressed in terms of its coefficients. This leads to the vertex formula showing the $x$ and $y$ coordinates of the vertex as the following: $\left(-\dfrac{b}{2a}, \dfrac{4ac – b^2}{4a}\right)$.

In the next section, learn how to use $-b/2a$ in finding the vertex of a parabola, the maximum and minimum points of functions, as well using it in optimization problems.

How To Use -b/2a in Vertex Formula?

To use the expression $-b/2a$ in the vertex formula, identify the coefficients of the quadratic function immediately. Use these values to find the exact value for $-b/2a$ then use this result to solve the given problem. The expression $-b/2a$ and the vertex formula have a wide range of applications, including:

1. Finding the vertex of a parabola given the quadratic function’s equation.

2. Identifying a parabola’s axis of symmetry using the equation $x = -b/2a$.

3. Solving optimization problems involving quadratic functions.

This section highlights the many uses of $-b/2a$ in the context of the vertex formula. 

How To Use -b/2a in Finding the Vertex of a Parabola

The expression $-b/2a$ represents the $x$-coordinate of the parabola’s vertex. This means that another way of finding the parabola’s $y$-coordinate is to evaluate the function at $x =-b/2a$. Given the quadratic function, $f(x) =ax^2 +bx +c$, the vertex of a parabola can be determined using either of the two formulas:

The two methods should return the same value for the vertex. Students can choose to apply either of the methods and it now all boils down to preference. The good thing about the first one is that it’s a straightforward approach as long as the correct formula is applied. If you’re already familiar with the quadratic formula, remembering the vertex formula will not be as challenging.

Meanwhile, the second method is more intuitive and only focuses on the easier expression: $-b/2a$. After finding the $x$-coordinate, simply evaluate the function at $x = -b/2a$ to find the vertex’s $y$-coordinate.

Example of Using -B/2A in Finding the Parabola’s Vertex

As an example, find the vertex of the parabola from the quadratic equation $y= x^2 – 6x + 13$.

Solution

For this problem, we should first use the expression $-b/2a$ and use the corresponding function’s coefficients to find the value of the vertex’s $x$-coordinate.

\begin{aligned}a&= 1\\b&= -6\\\\h &= -\dfrac{b}{2a}\\&=-\dfrac{-6}{2\cdot 1}\\&=3\end{aligned}

At this point, you have two options: evaluate the vertex’s $y$-coordinate using the first method or use the function and evaluate it when $x =3$. Here are two ways to find the $y$-coordinate of the vertex:

Hence, this example shows how, thanks to $-b/2a$, it’s now possible to find the parabola’s vertex using its corresponding quadratic equation. Take a look at the graph of the quadratic function $y= x^2 – 6x + 13$ below.

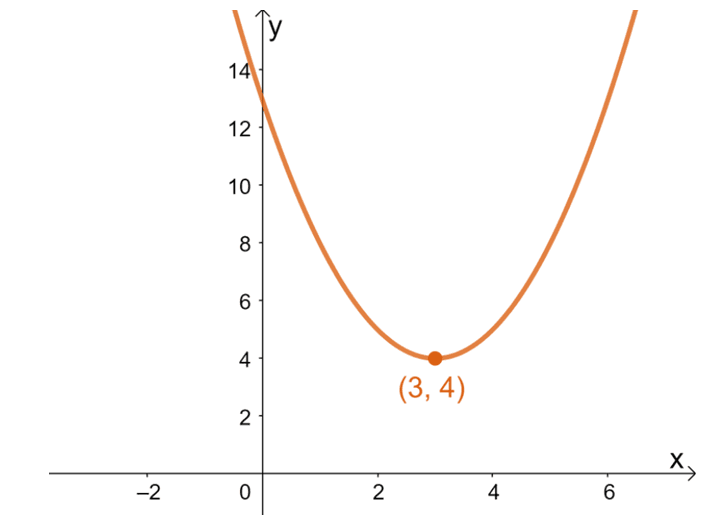
The graph also confirms the fact that the quadratic function’s vertex is $(3, 4)$. In fact, its vertex also represents the minimum point of the function. By using the vertex form and $-b/2a$, there is no need to graph the quadratic functions’ curves each time.

Here are some quadratic functions with their corresponding vertex. Try to work these out on your own to test your understanding.

Now $-b/2a$ is also essential when looking for the parabola’s axis of symmetry. The next section covers this to highlight the second application of the vertex formula and $-b/2a$.

Using -B/2A in Finding the Axis of Symmetry Example 1

The expression, $-b/2a$, is also crucial in finding the parabola’s axis of symmetry without graphing the function. When given a parabola or a quadratic function, the axis of symmetry is the line of symmetry passing through the parabola’s vertex. The general form of the axis of symmetry is $x = h$, where $h$ represents the parabola’s $x$-coordinate.

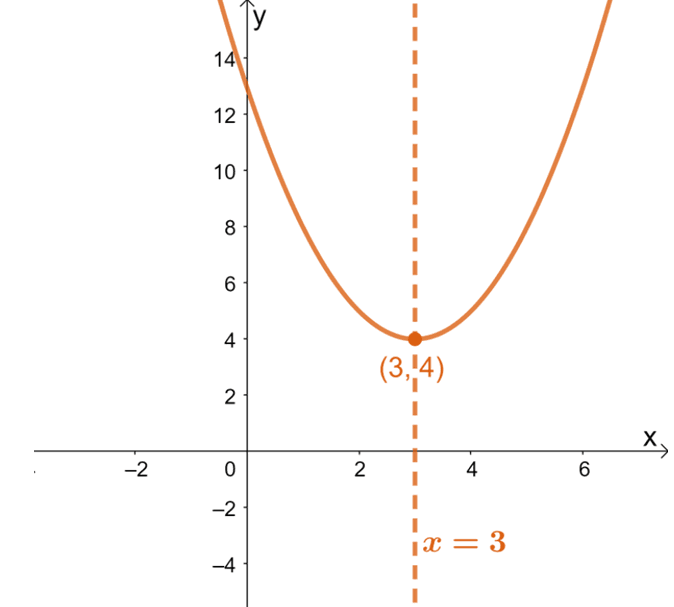
This means that the axis of symmetry of a quadratic function (and its parabola) can be defined by $-b/2a$. In fact, the axis of symmetry is $\boldsymbol{x = -\dfrac{b}{2a}}$. Here are some examples of quadratic functions with their corresponding axis of symmetry.

This also means that when given the quadratic function’s axis of symmetry, it is easy to find the coordinates of the function’s parabola. This is when the second method of finding the vertex’s $y$-coordinate comes in: given the axis of symmetry’s equation, evaluate the quadratic function at the given value of $x$.

Using -B/2A in Finding the Axis of Symmetry Example 2

Try this example where the vertex form of the quadratic function is given. Find the axis of the symmetry of the quadratic function $f(x) = 2(x – 2)^2 +5$.

Solution

Since the quadratic function is already in its vertex form, identify its parabola’s vertex first. Recall that given a quadratic function’s vertex form $y = a(x – h)^2 +k$, its vertex has coordinates at $(h, k)$. This means that the function $f(x) = 2(x – 2)^2 +5$ has a vertex at $\boldsymbol{(2, 5)}$.

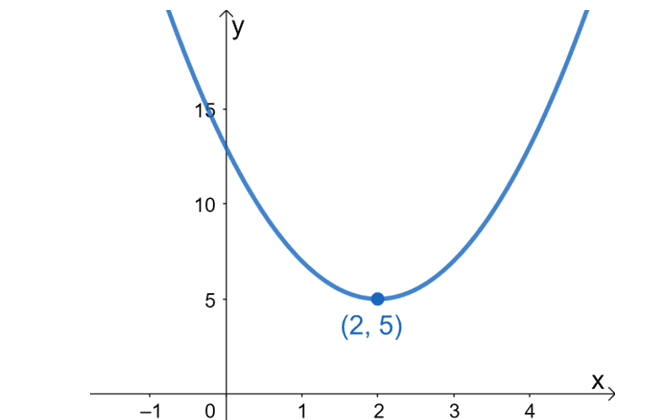
The $x$-coordinate of $f(x)$’s vertex is $2$, so using this, the axis of symmetry of the quadratic function has an equation of $x =2$.

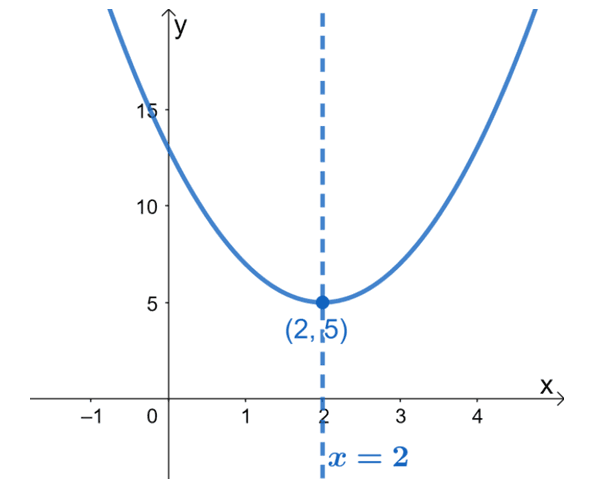
The graph of the quadratic function along with its axis of symmetry reflects that. As can be seen, the axis of symmetry divides the two sections of the parabola equally. This means that when given the vertex form of the quadratic function, it’s now easier to determine its axis of symmetry without graphing its curve.

-b/2a in Finding the Axis of Symmetry Example 3

Of course, not all quadratic functions are written in their vertex forms. When this happens, go back to the vertex formula to find the $x$-coordinate of the parabola. Use this approach (and the value of $-b/2a$) to find the axis of symmetry of $y = 3x^2 – 8x + 4$.

Solution

When the given quadratic function is in standard form, use the coefficients of the equation to find the value of $-b/2a$. For the quadratic function $y = 3x^2 – 8x + 4$, the coefficients are as follows:

\begin{aligned}y &= 3x^2 – 8x + 4\\a&= 3\\b&= -8\\c&= 4\\\\-\dfrac{b}{2a} &= -\dfrac{-8}{2\cdot3}\\&= \dfrac{4}{3}\end{aligned}

Since the axis of symmetry is defined by the vertex’s $x$-coordinate for quadratic functions of the form, $y = ax^2 + bx + c$, the axis of symmetry for $y= 3x^2 – 8x + 4$ is equal to $x = \dfrac{4}{3}$.

Aside from identifying the core components of the quadratic function and its parabola, the vertex formula and $-b/2a$ are also essential when it comes to solving problems that involve minimum and maximum points.

Why Is -b/2a Important in Common Optimization Problems?

The vertex formula, including the value of $-b/2a$, is essential in solving optimization problems involving quadratic functions because a parabola’s vertex reflects either the minimum or maximum point of the function, so the vertex’s coordinates are crucial when working on optimization problems.

Suppose that $y= ax^2 +bx +c$, use the value of $-b/2a$ and the vertex formula to find the value of the following:

1. The input value that returns the minimum or maximum value of the function. This is the vertex’s $x$-coordinate or the very topic of this article: $-b/2a$.

2. The maximum or minimum value of the function by evaluating the function at $x = -b/2a$ or using the vertex formula to find the $y$-coordinate.

Here are some examples of optimization problems that will benefit from the vertex formula.

This shows that as long as the optimization problem’s model returns a quadratic function, the vertex formula (and $-b/2a$) can be applied to find the values that you need. Try out these optimization problems to better appreciate the vertex formula and $-b/2a$.

Example of Using – b/2a in Finding the Optimum Point

The quadratic function $y =2(x -1)^2 +3$ is in vertex form. What is the minimum value of the function?

Solution

The function is already in its vertex form, so it’s much easier to find the value of the parabola’s vertex. Given the vertex form of the quadratic function $y= a(x -h)^2 + k$, the parabola’s vertex is $(h, k)$. This means that the vertex of the quadratic function $y= 2(x -1)^2+ 3$, is $(1, 3)$.

Take a look at the function’s graph and its parabola – this confirms that $(1, 3)$ is the vertex of the function as well as the minimum point of the graph. The $y$-coordinate of the function represents the optimal point (minimum or maximum point) of the function. For the case of $y =2(x -1)^2 +3$, its minimum value is equal to $y =3$.

Example of Using – b/2a in Finding the Maximum Profit

Suppose that the function $P(x)=-10x^2+ 20x +45$ represents the profit, in thousands, that Anna’s local café earns in a month. If $x$ represents the total number of customers, in thousands, each month, a) how many customers must enter Anna’s café so it enjoys a maximum profit? b) What is the maximum possible profit?

Solution

When finding the value of the maximum point, look for the function’s vertex. When the quadratic function is in its standard form, apply the vertex formula (that includes $-b/2a$) to find its parabola’s vertex. To find the number of customers that Anna’s café must entertain to meet the maximum profit, find the $x$-coordinate of $P(x)$’s vertex.

\begin{aligned}P(x)&=-10x^2+ 20x +45\\a&=-10\\b&=20\\c&=45\end{aligned}

This is where $-b/2a$ comes in because it represents the $x$-coordinate of the $P(x)$’ vertex.

\begin{aligned}-\dfrac{b}{2a} &= -\dfrac{20}{2\cdot-10}\\&= 1\end{aligned}

From this, $P(x)$ is at its highest value when $x =1$. What does this mean for Anna’s café? a) This means that Anna’s café must serve $1000$ customers to meet the maximum profit. Now, to calculate the maximum profit of the café using either of the two methods: 1) applying the vertex formula to find the $y$-coordinate or 2) evaluating $x =1$ into $P(x)$.

Method 1: Using the Vertex Formula Method 2: Evaluating the Quadratic Function

\begin{aligned}\dfrac{4ac – b^2}{4a}&=\dfrac{4\cdot-10\cdot 45- (20)^2}{4 \cdot -10}\\&= 55\end{aligned} \begin{aligned}x &= 1\\P(1) &= -10(1)^2+ 20(1) +45\\&=55\end{aligned}

Using any of the two methods leads to the same values, so the maximum value of $P(x)$ is $55$. b) Hence, the maximum profit that Anna’s café earns in a month is $\$ 55, 000$. Again, this only happens when they can serve $1000$ customers that month.

Example of Using -b/2A in Finding the Maximum Area

Harry is refurbishing his farm by building a fence around a plot of the rectangular area. One side does not require a fence since Harry is planning to use a wall as the fourth fence. If Harry invested in $1300$ feet of fence materials, a) what are the dimensions of the fenced plot to maximize its area? b) What is the largest area that the rectangular plot can have?

Solution

When working with word problems that involve geometric figures, it’s helpful to sketch an illustration to guide you in setting up the right expression for the plot’s area.

The dashed line represents the segment that does not need fencing. By taking a look at the illustration, it shows that the total amount fencing materials, in feet, is equal to $(2h + w)$. Rewrite $w$ in terms of $h$ by equating $(2h + w)$ to the total amount of fencing materials that Harry has.

\begin{aligned}(2h + w)&= 1300\\w&= 1300 – 2h\end{aligned}

Recall that the area of the rectangle is equal to the product of its length and width, so the function of its area can be defined in terms of $h$ (or $w$) as well.

\begin{aligned}A(h) &= h(1300 -h)\\&=1300h – h^2\\&=-h^2 + 1300h\end{aligned}

To find the dimensions of the rectangle that returns the maximum area for the plot, look for $A(h)$’s vertex by using the vertex formula starting with $-b/2a$. Find the height of the rectangle by calculating the value of $h = -b/2a$.

\begin{aligned}a&=-1\\b&=1300\\c&=0 \\-\dfrac{b}{2a} &= -\dfrac{1300}{2\cdot-1}\\&=650\end{aligned}

This means that for the plot to maximize its area, its height (or length) must be equal to $650$ feet. Now, use $w = 1300 -2h$ to finds the plot’s width.

\begin{aligned}w &= 1300-2h\\&= 1300 – 2\cdot 650\\&=650\end{aligned}

Hence, it would be smart if Harry fences a plot that is a square (which is a special type of rectangle) that measures a)$650$ by $650$ feet. Now, to find the measure of the area, either use the vertex formula for the $y$-coordinate or evaluate the $A(h)$ at $h = 650$. Let’s use the second method for this problem:

\begin{aligned}A(h) &= 650 \cdot 650\\&= 422, 500\end{aligned}

This shows that the largest area possible for the rectangular plot is b) $422, 500$ squared feet.

Conclusion

The expression $-b/2a$ plays a great role when working on parabolas, quadratic functions, and optimization problems. After going through this article, you can now feel more confident when finding the parabola’s vertex as well as solving problems involving quadratic functions. Why don’t we sum up everything we’ve discussed to ensure that you’re now ready and confident to use the vertex formula?

• When a quadratic function is in its vertex form, $y =a(x –h)^2 +k$, the vertex is located at $(h, k)$.

• When it is in standard form, $y = ax^2 +bx+c$, the vertex’s $x$-coordinate is equal to $-b/2a$ and its $y$-coordinate is equal to $\dfrac{4ac – b^2}{4a}$.

• This means that the parabola’s vertex is equivalent to $(h, k) =\left(-\dfrac{b}{2a}, \dfrac{4ac –b^2}{4a}\right)$.

• When finding the minimum or maximum value from an optimization problem, the parabola’s vertex plays an important role.

• Given the function’s vertex, its $x$-coordinate represents the input value that returns the optimum point.

With all these concepts in mind, you can now feel confident when dealing with problems involving quadratic functions, $-b/2a$, and the vertex of the function.