When Does a Quadratic Function Have No Real Solution?

A quadratic equation has no real solution if the value of the discriminant is negative.

When we find the roots of a quadratic equation, we usually come across one or two real solutions, but it is also possible that we don’t get any real solutions. In this article, we will discuss quadratic equations in detail and what happens when they don’t have real solutions, along with numerical examples.

When Does a Quadratic Function Have No Real Solution?

There are three different ways to tell whether the solution to a given quadratic equation is real or not, and these methods are calculating the discriminant, looking at the graph, and looking at the coefficients.

Calculating the Discriminant

The easiest way to tell that the given quadratic equation or function has no real roots is to calculate the value of the discriminant. If it is negative, then the quadratic equation does not have any real solutions. If the quadratic equation is given as $ax^{2}+bx +c = 0$, then we can write the standard form of the quadratic formula as:

$x = \dfrac{-b \pm \sqrt{b^{2}-4ac }}{2a}$

In this formula, the term $b^{2}- 4ac$ is called discriminant, denoting it as “$D$”. The quadratic equation can have three solutions depending on the value of “$D$”.

1. The solution is real if “$D$” is > 0. This means we have two distinct solutions.

2. If “$D$” is equal to zero, then we have a single real solution.

3. If “$D$” < 0, we will have two complex solutions. In this case, we do not get a real solution.

So, for a quadratic equation with complex solutions, the value of $b^{2}-4ac$ will be less than zero or $b^{2}< 4ac$. Let us compare examples for each case of the discriminant.

You can verify these solutions by putting the values of a, b, and c in the quadratic formula. From the above table, we can deduce that whenever $b^{2}< 4ac$, we will only get complex roots.

Looking at the Graph

The second method to tell whether the quadratic equation or function has any real solution or not is by looking at the graph of the function or equation. The graph of any quadratic equation will be a parabola or bell-shaped, and we know the most important feature of a parabola is its vertex.

The shape of the vertex of the parabola depends upon “$a$”; if the value of “$a$” is negative, then the shape of the vertex is like a mountain top or peak. If the value of “$a$” is positive, then the shape is like a valley bottom at the bottom of the mountain. A quadratic equation graph with complex solutions will not touch the x-axis.

The parabola can be completely above or below the x-axis if the equation has complex solutions. When the value of $a<0$, the parabola will be below the x-axis; when $a>0$, the parabola will be above the x-axis. Let us draw the graph for three equations discussed in the previous section.

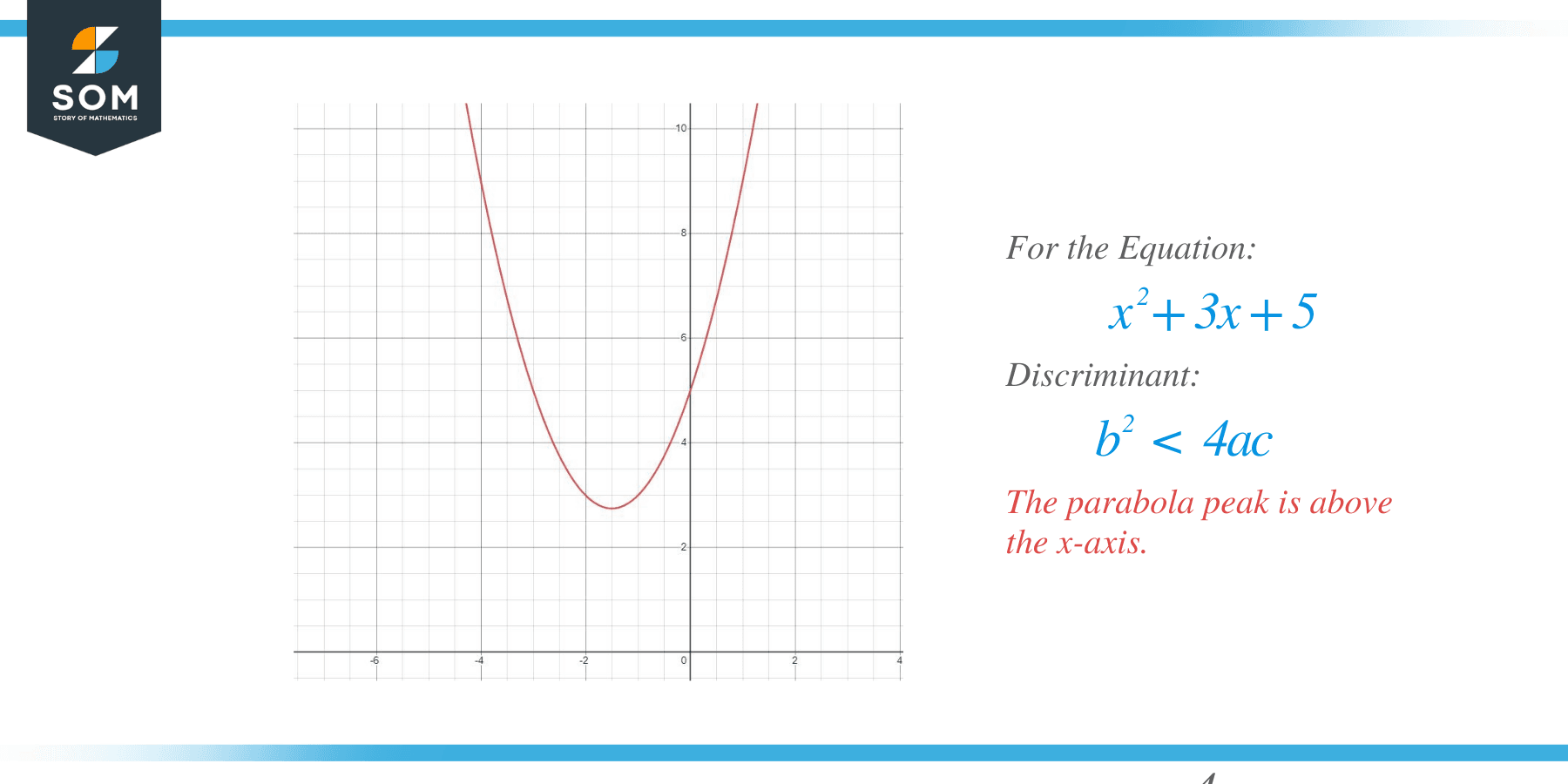
For the equation $x^{2}+ 3x + 5$, we know all solutions are complex, and as we can see below, the graph is above the x-axis as “a” is greater than zero. The graph is not touching the x-axis, so if you are provided with a graph and you are asked to tell whether the function has real solutions or not, you can instantly tell if the graph is not touching the x-axis then it will only have complex solutions.

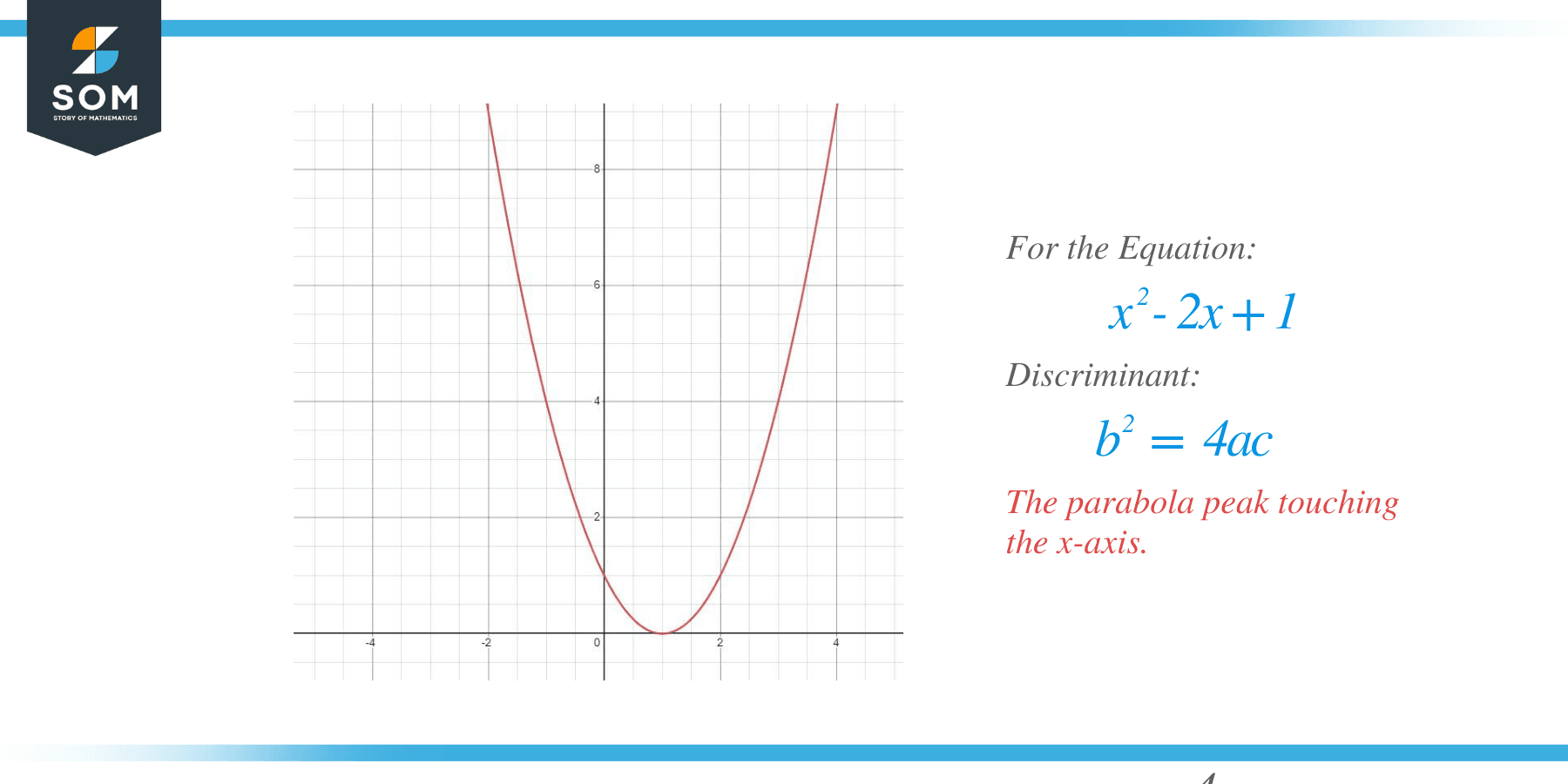
For the equation $x^{2}-2x +1$, we know the value of the discriminant is equal to zero; for this case, the parabola peak will always touch the x-axis. It will not go across the x-axis; the peak will land on the x-axis, as shown in the figure below.

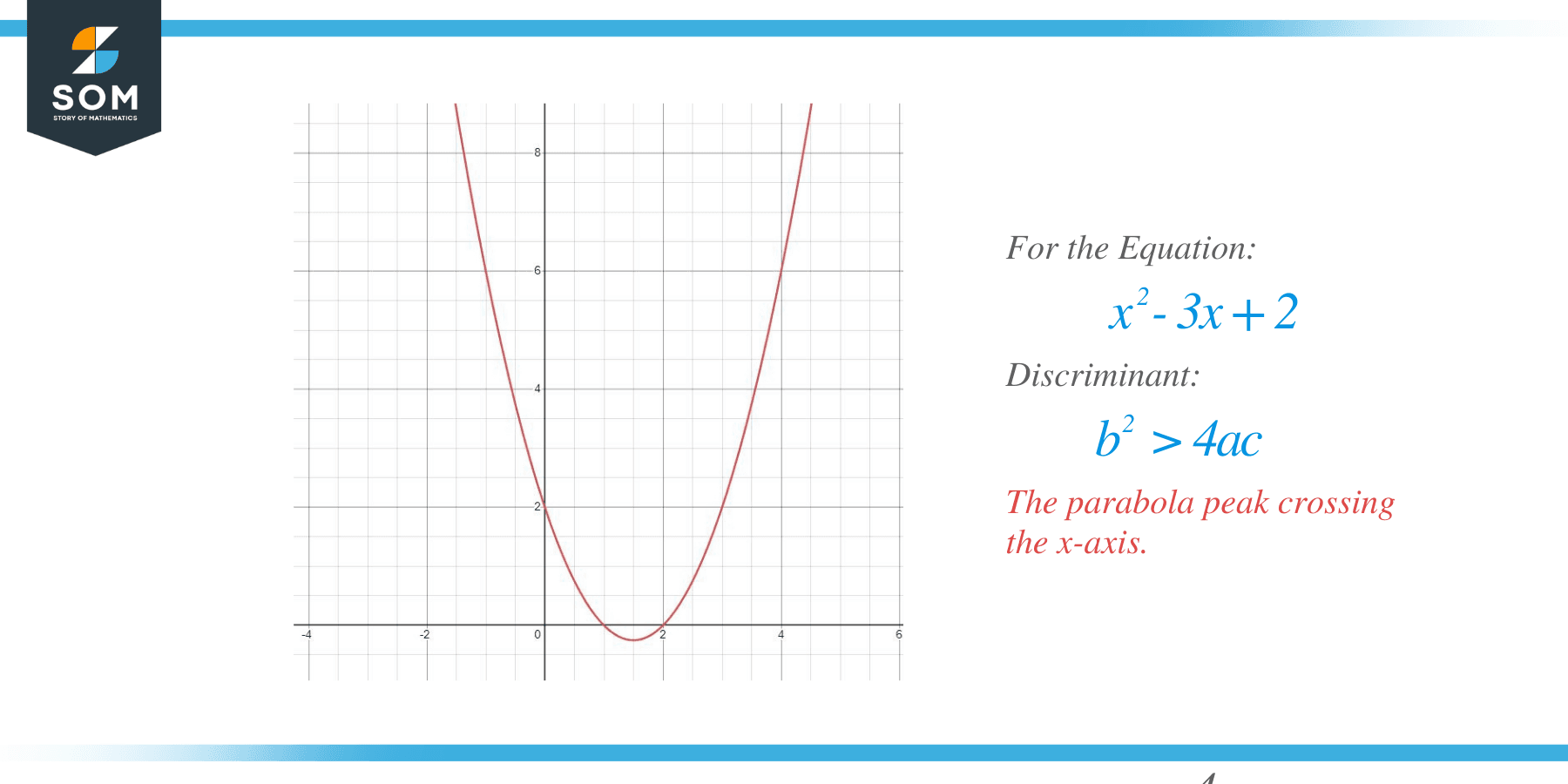
For the equation $x^{2}-3x +2$, we know the value of the discriminant is greater than zero; for this case, the parabola peak will cross the x-axis. If the value of $a > 0$, then the peak value or mountain top will be going down the x-axis and if the value of $a < 0$, then the peak value or mountain top will be above the x-axis. We show the graph below.

Looking at the Coefficients

In the third method, we look at the coefficients of the given equation. Remember the equation should be given in the normal quadratic equation form as $ax^{2}+bx + c = 0$.

We can only use this method in special circumstances, for example, when we are not provided with the value of “$b$” or the value of “$b$” is equal to zero. Furthermore, the sign of the coefficients “$a$” and “$c$” must also be the same. For $b = 0$, if both “c” and “a” are positive then $\dfrac{c}{a}$ is positive and -\dfrac{c}{a} is negative and similarly if both “c” and “a” are negative then $\dfrac{c}{a}$ is positive and $-\dfrac{c}{a}$ is negative. In both cases, taking the square root will give us two complex solutions.

Let us take an example of the quadratic equation $x^{2}+ 6 = 0$, we can see that in this equation $a = 1$, $b = 0$ and $c = 6$. The roots for given equation are $2.449i$ and $-2.449i$.

Similarly, if we take the example of quadratic equation $-3x^{2}- 6 = 0$, we can see that in this equation $a = -3$, $b = 0$ and $c = -6$. The roots for the given equations are $1.41i$ and $-1.41i$. So, we can see that when signs of coefficients “$a$” and “$c$” were the same and b was equal to zero, we only get complex solutions.

Does the Quadratic Equation Always Have a Solution?

Yes, the quadratic equation will always have a solution that can either be complex or real. The quadratic equation can have a maximum of $2$ real solutions. So the real solution for a quadratic equation can be $0$,$1$, or $2$, depending upon the type of quadratic equation. Similarly, the quadratic equations’ complex roots can be $2$ or zero. We can summarize the roots of the quadratic equation as follows:

• When the value of the discriminant is positive, then we will have two real solutions.

• When the value of the discriminant is equal to zero, we will have a single real solution.

• When the value of the discriminant is negative, we will have two complex solutions.

Examples of Quadratic Equations

Let us now study examples by solving quadratic equations having real or complex solutions. We will study no real solution quadratic equation examples and real solution quadratic equation examples.

Example 1: Solve the quadratic equation $x^{2}+ 2x + 2$

Solution:

We know for the given quadratic equation the value of $a =1$, $b = 2$ and $c =24$

The value of $b^{2}= 2^{2}= 4$

$4ac = 4 (1)(2) = 8$

$b^{2}- 4ac = 4 – 8 = -4$.

As the value of discriminant is less than zero, then this equation will only have complex solutions. Let us put the value of a, b and c in quadratic formula and solve for the roots to verify.

$x = \dfrac{-2 \pm \sqrt{-4 }}{2(1)}$

$x = -1 \pm 1i$

Example 2: Will the quadratic equation $-2x^{2}+4 = 0$ have real roots or not?

Solution:

We know for the given quadratic equation the value of $a = -2$, $b = 0$ and $c =4$.

We have studied that if a quadratic equation does not have the coefficient “$b$” or the value of “$b$” is equal to zero and the sign of coefficient “$a$” and “$b$” are the same as well, then it will not have a real solution. But in this case, the sign of “$a$” and “$b$” are opposite, so this equation should have real roots.

$b = 0$

$4ac = 4 (-2)(4) = -32$

$b^{2}- 4ac = 0 – (-32) = 32$.

As the value of the discriminant is positive, it is the second indicator that tells us that this quadratic equation will have real roots. Let us put the value of a, b, and c in the quadratic formula and solve for the roots to verify.

$x = \pm\dfrac{ \sqrt{32 }}{2(-2)}$

$x = \pm \sqrt{2}$

Hence, we have proved the equation has real roots.

Example 3: Will the quadratic equation $-2x^{2}- 4 = 0$ have real roots or not?

Solution:

We can tell by just looking at the equation that it is a no real roots.

We know for the given quadratic equation the value of $a = -2$, $b = 0$ and $c = – 2$.

As discussed earlier, if the value of $b = 0$ and “$a$” and “$b$” have same sign, then there will be no real roots for the given equation and this equation fulfills all the criteria.

$b = 0$

$4ac = 4 (-2)(-4) = 32$

$b^{2}- 4ac = 0 – (32) = -32$.

As the value of the discriminant is negative, it is the second indicator that this quadratic equation will not have real roots. Let us put the value of a, b and c in the quadratic formula and solve for the roots to verify.

$x = \pm\dfrac{ \sqrt{-32 }}{2(-2)}$

$x = \pm \sqrt{2}i$

Hence proved the equation has no real roots

Example 4: Solve the quadratic equation $x^{2}+ 5x + 10 = 0$

Solution:

We know for the given quadratic equation the value of $a =1$, $b = 5$ and $c = 10$

The value of $b^{2}= 5^{2}= 25$

$4ac = 4 (1)(10) = 40$

$b^{2}- 4ac = 25 – 40 = -15$.

As the value of discriminant is less than zero, then this equation will not have any real solutions. Let us put the value of a, b and c in quadratic formula and solve for the roots to verify.

$x = \dfrac{-5 \pm \sqrt{-15 }}{2(1)}$

$x = -2.5 \pm 1.934i$

You can verify your answer quickly by using a no-real solution calculator online.

How To Write a Quadratic Equation Using the Complex Roots

It is quite easy to write a quadratic equation if you are provided with the complex roots. Suppose we are given the roots of the equation as $4i$ and $-4i$ and we are asked to find the original quadratic equation. We can do that by using the formula $(x-a) (x-b)$ let $a = 4i$ and $b = -4i$.

$(x- 4i) (x-(-4i)$

$(x-4i) (x+4i)$

$x^{2}- 16i^{2}$

$x^{2}-16(-1) = x^{2}+ 16$. So the quadratic equation for roots $4i$ and $-4i$ is $x^{2} +16$.

Frequently Asked Questions

What Is a Real Solution?

A real solution is a solution to an equation that only contains real numbers. In literature, you will often learn that if a quadratic equation discriminant is less than zero, it does not have a solution. It means that it does not have a real solution.

What Is a Non-real Solution?

A solution that contains imaginary numbers or is written in the form $a+bi$ is called a non-real or complex solution. Here, “a” is real, and the coefficient “b” has iota attached to it, which makes the term imaginary.

How Can a Quadratic Equation Have No Solution?

The quadratic equation will always have a solution. It will either be real or complex, but there will always be roots for the equation.

Conclusion

Let us conclude our topic discussion and summarize what we have learned so far.

• Quadratic equation will always have a solution, and it can either be real or complex depending upon the value of the discriminant.

• There will be no real roots if the value of discriminant is less than zero or $b^{2}-4ac < 0$ or $b^{2} < 4ac$.

• When the value of the discriminant is less than zero, we will have two complex solutions and no real roots

After studying this guide, we hope you can quickly identify when a quadratic has real solutions and when it only has complex solutions.