JUMP TO TOPIC
 To find the volume of a composite solid, we add the volumes of all the solid figures combined that make the composite solid.
To find the volume of a composite solid, we add the volumes of all the solid figures combined that make the composite solid.
The calculated volume then can also be used to calculate the surface area of the solid further. In this guide, we will learn what a solid is, how you calculate its volume, what it means by a composite solid, and how we calculate the volume of a composite solid. We will study various numerical examples so that you can grasp the concept of composite solids. At the end of the topic, you will be equipped with techniques to calculate the volume of composite solid figures.
What Is Composite Solid?
A composite solid is a solid that consists of two or more solids. If we combine two or more solids such that one solid is at the bottom and the other is at the top or if one solid is inside the other solid, then such figures are termed as composite solids.
A solid is a geometrical figure that can only be drawn in a three-dimensional plane. For example, cones, pyramids, right prims, rectangular prisms, cylinders, and spheres are all considered solid figures.
How To Calculate the Volume of a Composite Solid
We can calculate the volume of a composite solid by adding the individual volume of all the solid figures that combine to form the composite solid. For example, suppose a sphere and a prism combine so that the sphere is at the bottom and the prism is at the top to form a composite solid. In that case, we will add the individual volumes of both figures, and the resulting amount will be the volume of the composite solid.
A question arises: Do we always add the volumes of two or more figures combined to form a composite solid? The answer is no. If a solid figure is given inside another figure, then to calculate the volume of the composite solid, we subtract the figure with the larger volume from the figure having a smaller volume (as the volume of a figure cannot be negative). The steps to find the volume of a composite solid are given below.
Step 1: The first step is to measure the dimensions or write down the given solid figures’ dimensions.
Step 2: In the second step, calculate the volume of the individual solids. For example, if you are a composite solid consisting of a cone and cylinder, you have to individually find out the volume of the cone and the cylinder first.
Step 3: Determine whether you have to add the volume of both figures or subtract them. If one figure is at the top of the other, you add the volume of both figures, but if one figure is inside the other figure, you subtract the smaller figure’s volume from the larger one.
Volume Formulae for Different Solids
It is essential that you must know the volume formulas for each solid figure because without knowing the formula, you cannot solve questions related to composite solids. We can also use the volume of a composite figure to determine the surface area. This section will present the volume formulas for several solids mostly used in composite solid numerical.
Volume of a cylinder: The cylinder, if examined microscopically, can be seen as the stacking of numerous circular discs one over another. If we calculate the space acquired by each disc in the stack and add them up, it will give us the volume of the cylinder. Simply put, the volume of the cylinder is, therefore, the product of the area of the base of the cylinder and the height of the cylinder, and it is written as:
Volume of the cylinder $= Area \hspace{1mm} base \times height$
Volume of the cylinder $= \pi.r^{2}.h$
Volume of a cone: The cone is a three-dimensional figure, and its volume defines its full capacity. The cone has a circular base, and two-line segments from this base are combined at a common point called the apex point. We can write the formula for the cone as:
Volume of the cone $= \dfrac{1}{3}\pi.r^{2}.h$
Volume of a prism: The prism is a three-dimensional figure, and the prism’s volume is equal to the total amount of space inside a prism. Prism has various types, so the formula for the volume of the prism depends upon the type of the prism that is given in the numerical. Some of the types of a prism are:
1. Triangular prisms
2. Rectangular Prisms
3. Square prisms
4. Trapezoidal prisms
The volume of the prism will depend upon the base, if it is a square prism, then the area of the square will be multiplied by the height of the prism, and similarly, if it is a triangular prism, then the area of the triangle will be multiplied with the height of the prism. We can write the general formula for the volume of the prism as:
Volume of the prism $= Area (base\hspace{1mm} area) \times height$
Volume of a sphere: The sphere is a three-dimensional solid figure, and the volume of a sphere is equal to the total space within a sphere. The sphere may look like a circle, but a circle is a two-dimensional figure. Suppose we rotate a circle in a three-dimensional plane. In that case, it will give us a sphere as each point on the surface of the sphere is equidistant from the center of the sphere, similar to the case of a circle where each point on the boundary is equidistant from the center of a circle. We can write the formula for the volume of a sphere as:
Volume of the sphere $= \dfrac{4}{3}\pi.r^{3}$
Volume of a pyramid: The volume of a pyramid is equal to the total space inside a pyramid. A pyramid is considered a part of a prism since the volume of the pyramid is one-third of the prism’s volume. The bases of a prism and pyramid are considered congruent, while their height is considered the same. So, if we add three similar types of pyramids, it will give us a prism; similarly, combining three rectangular pyramids will provide us with a rectangular prism. We can write the formula for the volume of a pyramid as:
Volume of a pyramid $= \dfrac{1}{3}Base \times height$
Volume of a Composite Solid Examples
Let us now study various examples of finding the volume of different composite figures.
Example 1: Determine the volume of the composite solid given below.
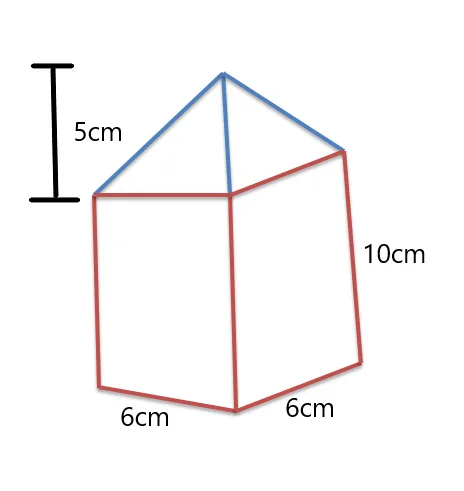
Solution:
We are given a square prism, and the bases are all square. We are also given the square prism’s height and the pyramid’s height at the top.
The formula for the volume of the square prism is:
Volume $= area\hspace{1mm} of\hspace{1mm} square \times height\hspace{1mm} of\hspace{1mm} the \hspace{1mm}prism$
Area of the square $= 6^{2} = 36 cm^{2}$
Volume of the prism $= 36 \times 10 = 360 cm^{3}$
Now, we calculate the volume of the pyramid at the top, it has a square base, so the area of the base is the same as $36^{2}cm^{2}$.
Volume of the pyramid $= Area \hspace{1mm} of\hspace{1mm} the \hspace{1mm}base \times height\hspace{1mm}of\hspace{1mm} pyramid$
Volume of pyramid $= 36 \times 5 = 180 cm^{3}$
Composite solid formula for volume $= volume\hspace{1mm} of\hspace{1mm} prism + volume\hspace{1mm} of\hspace{1mm} the\hspace{1mm} pyramid$
Volume of the composite solid $= 360 + 180 = 540 cm^{3}$
Example 2: The figure given ( composite solid) below has square bases. You are required to determine the volume of the composite solid.
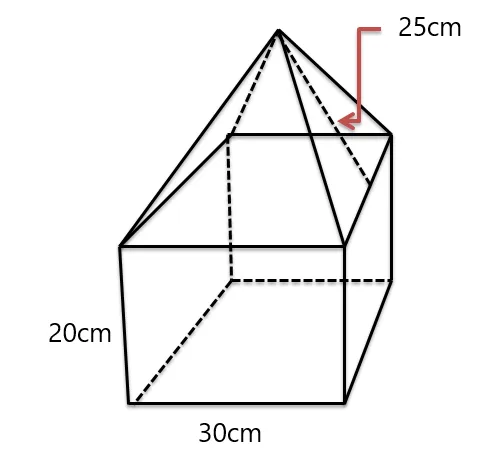
Solution:
First of all, we have to determine the types of figures which we are provided with. As the shape suggests, the top figure is a pyramid with a square base, and the bottom figure is a square pyramid.
The formula for the volume of the square prism is:
Volume $= area \hspace{1mm} of\hspace{1mm} square \times height\hspace{1mm} of \hspace{1mm}the\hspace{1mm} prism$
We know that we can calculate the area of the square by multiplying two sides of the square. As all the sides of the square are the same, the length of one side is given in the figure as 30cm.
Area of the square $= 30 \times 30 = 900cm^{2}$
Volume of the square prism $= 900 \times 20 = 18,000 cm^{3}$
The next step is to calculate the volume of the square pyramid, and to do that, we need the height of the pyramid. We will use the Pythagoras theorem to determine the pyramid’s height. We can see the perpendicular dotted line drawn on the pyramid so its divides the base into two halves of 15 cm each, so the height of the pyramid is:
Height $= \sqrt{25^{2}-15^{2}} = 20 cm$
Volume of the pyramid $= \dfrac{1}{3}Area\hspace{1mm} of\hspace{1mm} square \hspace{1mm}(base) \times height$
V $= \dfrac{1}{3}\times 30^{2}\times 20 = 6000 cm^{3}$
So we can calculate the volume of the composite solid by adding the volume of the square prims and pyramid:
Volume of the composite solid $= 18000 + 6000 = 24,000 cm^{3}$
Example 3: You are given a tissue roll with dimensions shown in the figure below. Determine the volume of the tissue roll.
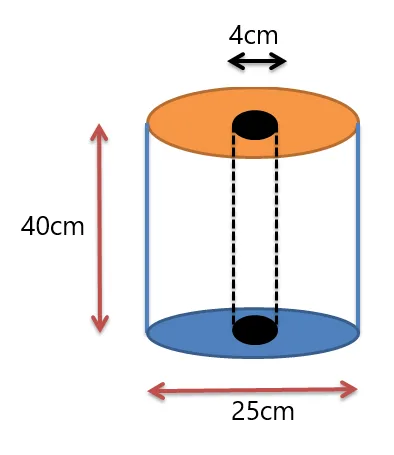
Solution:
We are given two cylinders. One cylinder is the roll and the second cylinder is the hole in the center of the roll. So we will determine the volume of both cylinders and then subtract the volume of the hole from the volume of the outer roll.
Volume of a cylinder $= \pi.r^{2} \times height$
The volume of the big cylinder $= \pi. (\frac{25}{2})^{2} \times 40$
The volume of the big cylinder $= \pi. (12.5)^{2} \times 40$
The volume of the big cylinder $= 6250 \pi cm^{2}$
Now we calculate the volume of the hole or smaller cylinder
Volume of the hole $= \pi. (\frac{4}{2})^{2} \times 40$
Volume of the hole $= \pi. 4 \times 40 = 160 \pi cm^{3}$
Volume of the composite solid $= \pi(6250 -160) = 6090 \pi cm^{3}$
Example 4: Suppose you are given a picture of a tree with a tiny cylindrical trunk while the bushes form a sphere at the top. You are required to calculate the volume of the tree as a whole.
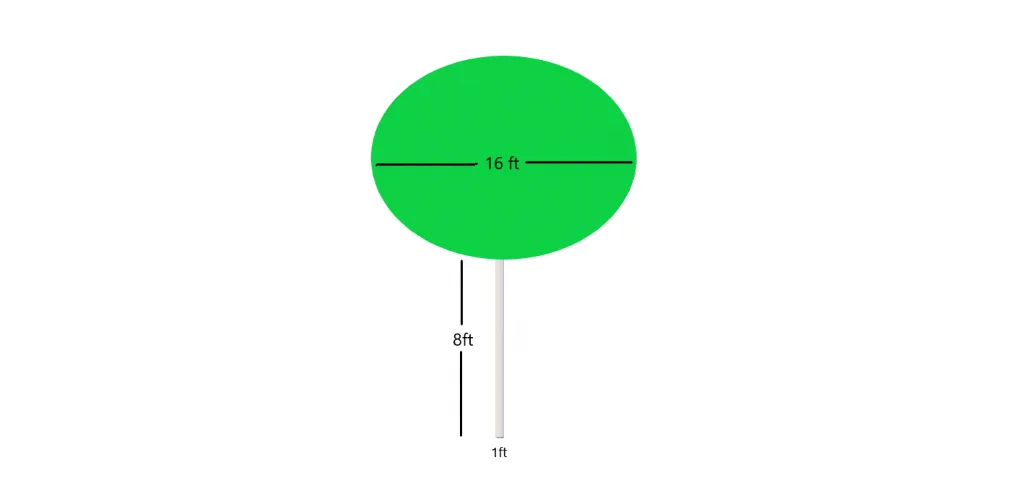
Solution:
The lower part or trunk of the tree is a cylinder and we know:
Volume of a cylinder $= \pi.r^{2} \times height$
The volume of the big cylinder $= \pi. (\frac{1}{2})^{2} \times 8$
The volume of the big cylinder $= \pi. 0.25 \times 8$
The volume of the big cylinder $= 2 \pi cm^{3}$
The bushes of the tree form a sphere, and the volume for the sphere is given as
Volume of the bush $= \dfrac{4}{3}\pi.r^{3}$
Volume of the bush $= \dfrac{4}{3}\pi.(8)^{3}$
Volume of the bush $= 682.6\pi$
The volume of the tree $= \pi (682.6 + 2) = 684.6 \pi cm^{3}$
Example 5: Find out the volume of the composite solid figure given below.
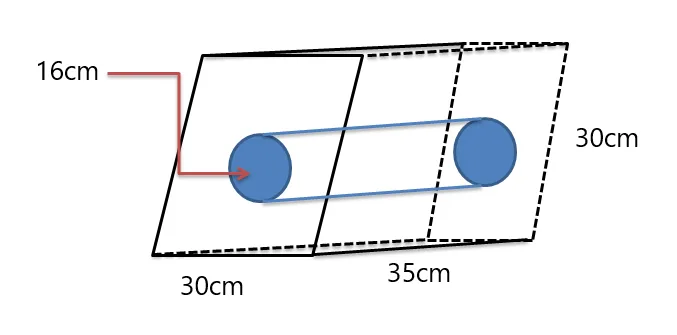
Solution:
We are given parallelogram prims while a cylinder is cut out in the middle of the prism. So, we will first find out the volume of both solids, then we will subtract the volume of the cylinder from the volume of the prism (as the prism has the larger volume as seen in the figure).
Volume of the prism $= 30^{2} \times 35$
Volume of the prism $= 900 \times 35 = 31,500 cm^{3}$
Volume of the cylinder $= \pi. (8)^{2} \times 35$
The volume of the big cylinder $= 2240 \pi cm^{3}$
Volume of the composite solid $= 31,500 – 2240.\pi \cong 24462 cm^{3}$
Conclusion
Let us summarize the key points that we have learned from this guide.
• A composite solid is a three-dimensional figure.
• A composite solid is a collection of two or more solid figures.
• To determine the volume of a composite solid, we must find out the individual volume of the combined figures. If one figure is on the top of the other figure, we add the volume of both figures, and if one figure is inside the other, then we subtract the smaller volume from the bigger or higher volume.
After studying this guide, you should now feel more confident that you understand the different types of composite solids, and you can also determine the volume of each type.
