The Cavalieri’s Principle relates the volumes of two solids given their cross-sections and heights. This principle is also helpful when comparing the areas of two solids given their respective bases and heights. Understanding Cavalieri’s Principle leads to a wide range of properties shared by two and three-dimensional figures.
Cavalieri’s Principle states that when the two solids share identical cross-sections and heights, their volumes are equal. These solids must meet the conditions set for the principle before making this conclusion.
This article covers the conditions needed to apply Cavalieri’s Principle and how the principle extends to surfaces and solids. This discussion also covers examples and applications of Cavalieri’s Principle.
What Is Cavalieri’s Principle?
Cavalieri’s Principle is a principle stating that the volumes of two or more solids are equal when they share the same areas and lengths for their cross-sections and heights, respectively. This principle is also applicable for two-dimensional figures — the concept behind how areas of parallelograms and triangles are established relies on Cavalieri’s Principle.
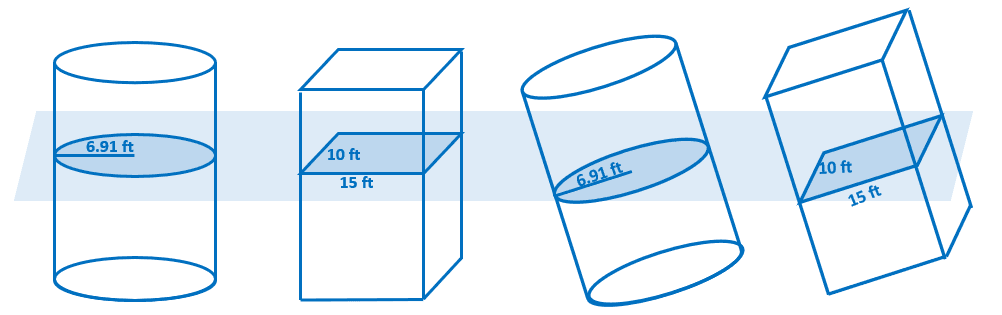
Take a look at the four solid figures shown above and suppose that each solid has a height of $h$. The Cavalieri’s Principle states that if their cross-sectional areas and heights are the same, the volumes of four solid figures are going to be the same.
Starting from the left, label the upright cylinder’s volume as $V_A$, the second rectangular prism as $V_B$, and so on.
\begin{aligned}\boldsymbol{V_A}\end{aligned} | \begin{aligned}\boldsymbol{V_A} &= \pi(6.91^2)(h)\\&\approx 150h\end{aligned} |
\begin{aligned}\boldsymbol{V_B}\end{aligned} | \begin{aligned}\boldsymbol{V_B} &= 10(15)(h)\\&= 150h\end{aligned} |
\begin{aligned}\boldsymbol{V_C}\end{aligned} | \begin{aligned}\boldsymbol{V_C} &= \pi(6.91^2)(h)\\&\approx 150h\end{aligned} |
\begin{aligned}\boldsymbol{V_D}\end{aligned} | \begin{aligned}\boldsymbol{V_D} &= 10(15)(h)\\&= 150h\end{aligned} |
Calculating the individual volumes of the solids confirm the fact that with cross-sections having identical areas ($150$ square feet) and heights, their volumes are going to be equal. Explore the fundamentals of Cavalieri ‘s Principle by understanding how it applies to two-dimensional and three-dimensional figures.
Understanding the Cavalieri’s Principle and Area
When given two flat surfaces, the Cavalieri’s Principle still applies when the two surfaces meet the following conditions:
- The two surfaces that are being observed are contained within a pair of parallel lines lying along the plane.
- The additional parallel lines that intersect within the two regions divide the segments with equal lengths.
When two surfaces meet these conditions, Cavalieri’s Principle states that their areas are equal. Imagine that a quadrilateral similar to the figure shown below is cut into stacks. The second image is the result when the rectangle’s stacks are slightly pushed to the right, forming a more slanted shape. Now the question is, will their areas be the same?
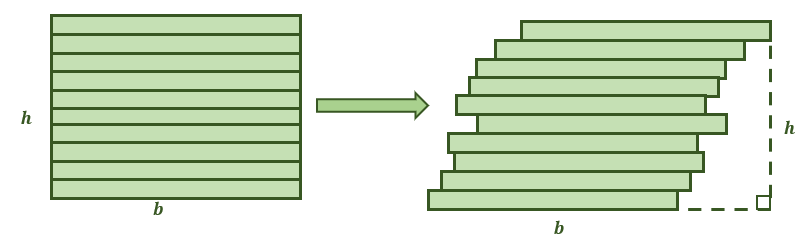
This is when Cavalieri’s Principle comes in handy for two-dimensional figures and their areas. The two planes’ opposite sides are parallel to each other.
In addition, if each of the figures is divided into smaller stacks by additional parallel lines, each of the segments is congruent. This means that the conditions are met for Cavalieri’s Principle, so their areas are expected to be equal.
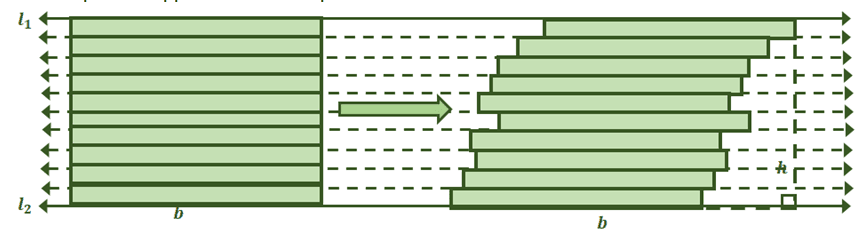
Extending this concept for parallelograms and rectangles, we now know that when they share the same bases and height, their areas will also be equal.
Understanding the Cavalieri’s Principle and Volume
The Cavalieri’s Principle is often associated with equating the volumes of two solids that share identical cross-section areas and heights.
Suppose that two solids meet the following conditions:
- Each of the three-dimensional figures is contained within two parallel planes.
- The solid is divided into identical surfaces by every additional parallel plane and these surfaces’ areas are equal.
The Cavalieri’s Principle applies, so the volumes of these two solids will be equal. To understand how this is possible, begin by imagining two stacks of coins with the second stack of coins arranged more neatly.
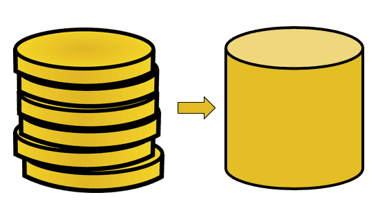
Suppose that all the coins share the same volume, regardless of how neatly stacked these coins are, the volume of the six coins will remain constant.
What do these two arrangements have in common?
- The cross-section or area of the coin’s face will always be equal.
- Since they are stacked with the same number of coins, the height of the two stacks is equal.
These sound familiar, right?
These are similar to the conditions set by Cavalieri’s Principle. When the two solids’ cross-sectional areas and heights are the same, their volumes are also identical.
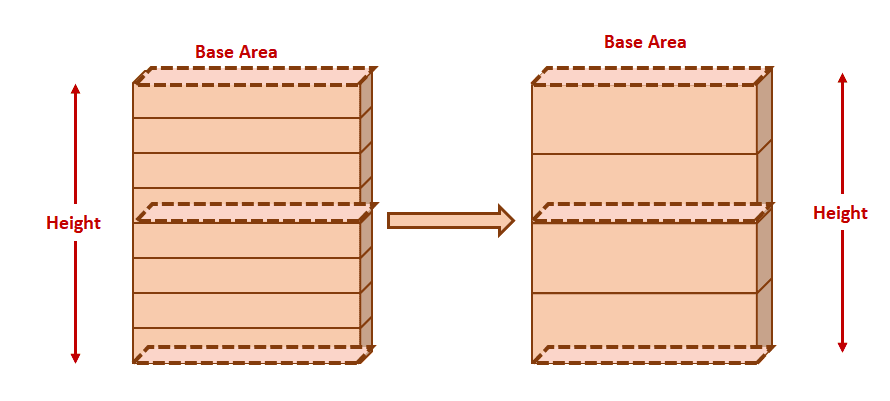
Take a look at the solid figures shown above — the parallel planes cutting the solids each have equal areas. These two solids are also contained by parallel planes, so Cavalieri’s Principle applies.
This means that the volumes of the two solids are equal.
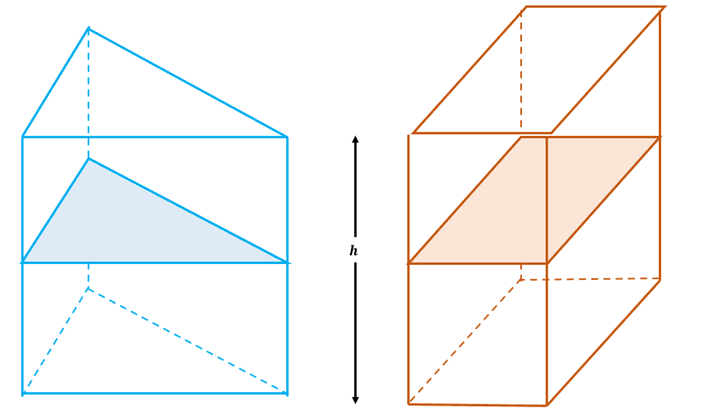
When given two three-dimensional figures with different shapes, the Cavalieri’s Principle will still come in handy.
\begin{aligned}\text{Base Area}_1 &= \text{Base Area}_2\\\text{height} &= h\\(\text{Base Area}_1)(h)&=(\text{Base Area}_1)(h)\\\text{Volume}_1 &=\text{Volume}_2\end{aligned}
As long as the height and the base area of each of the solids’ cross-sections are the same, their volumes are equal. Now that the Cavalieri’s Principle has been established, learn how to apply them when working with two-dimensional and three-dimensional figures.
Cavalieri’s Principle Example
There are different examples of applications involving Cavalieri’s Principle such as 1) deriving formulas for the figures’ areas, 2) finding the volume of solids, and 3) applying the principle in calculus!
When applying Cavalieri’s Principle, always observe whether the cross-sections are identical for each level. When the height and the cross-sectional areas are equal, see whether Cavalieri’s Principles will be helpful for the particular problem.
Cavalieri’s Principle in 2D Figures
When applying Cavalieri’s Principle in 2D figures, review the conditions needed for two dimensions. These come in handy when confirming the areas of two particular figures or the general formulas for the areas of surfaces.
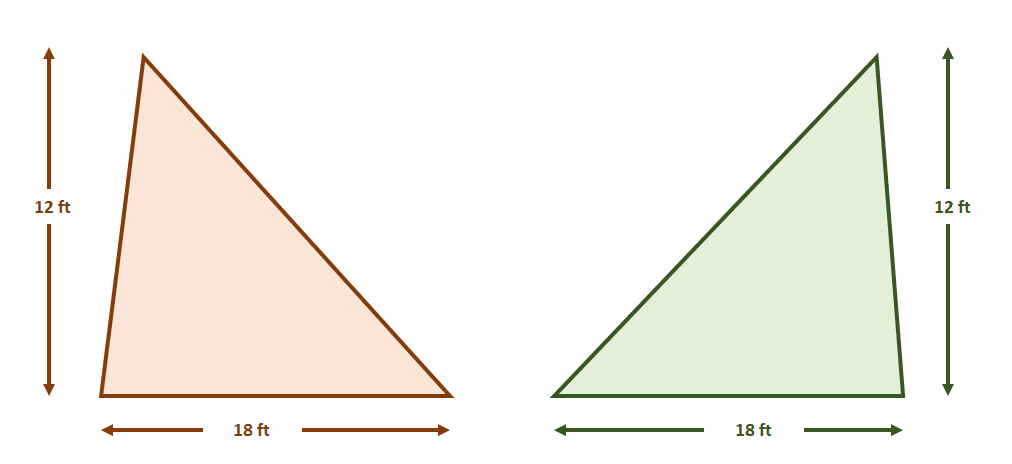
Now construct the pair of parallel lines that contain both triangles. Divide each of the figures with equal segment lengths using additional parallel lines as shown below. The triangles’ heights are also equal.
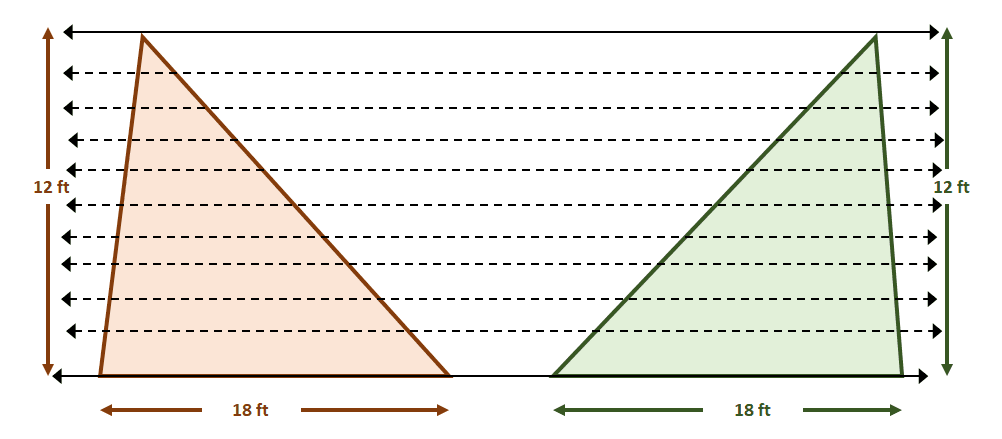
Since the figures meet the conditions for Cavalieri’s Principle, the areas of the two figures are equal. This makes sense since $A_{\text{Triangle}} = \dfrac{1}{2}bh$, so both triangles will have areas of $108$ square feet each.
Cavalieri’s Principle in 3D Figures
Cavalieri’s Principle is helpful when working with problems involving 3D figures. The two solids must meet the conditions of Cavalieri’s Principle before using it to solve these problems.
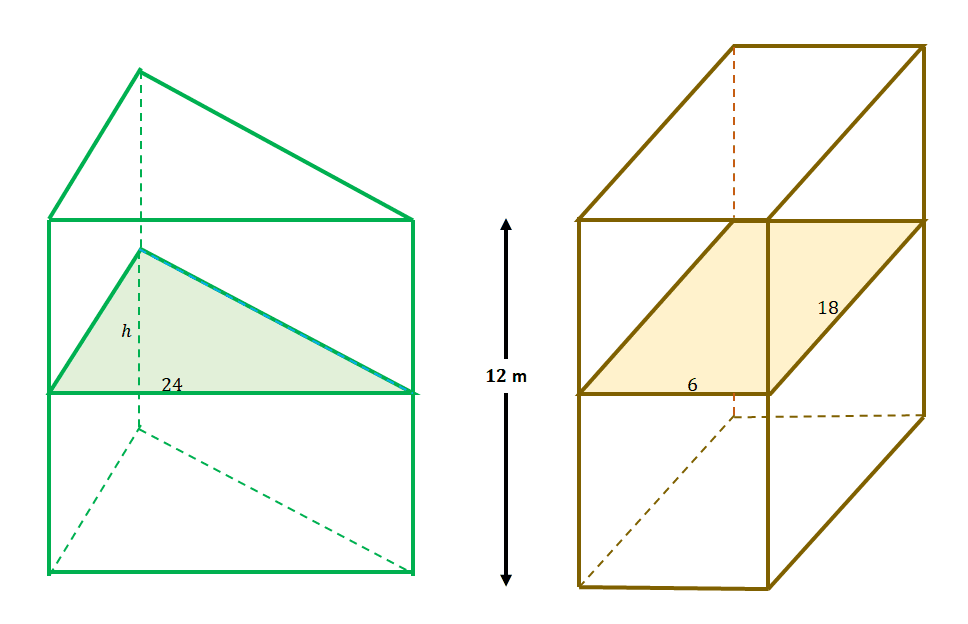
For example, these two solids meet the conditions of Cavalieri’s Principle: 1) they are contained between parallel planes and 2) the additional planes divide the cross-sections equally as shown from the previous problem.
This means that the cross-sectional areas are equal for the two solids. Equate the expression for each of the cross-section’s areas to solve for $h$.
\begin{aligned}A_{\text{Triangle}} &= A_{\text{Rectangle}}\\\dfrac{1}{2}(h)(24) &= 6(18)\\h&= \dfrac{2(6)(18)}{24}\\&= 9\end{aligned}
This means that the height of the triangle $h$ is $9$ meters long.
Cavalieri’s Principle in Integral Calculus
Integral calculus deals with slices and partitioned portions of surfaces and solids, so the Cavalieri Principle applies even for advanced topics such as integrals and volumes of solids. The Cavalieri’s Principle is most helpful when the cross-sectional areas of the solid are all equal.
Finding the Volume Using Cavalieri’s Principle
\begin{aligned}\text{Volume}_{S} = \int_{a}^{b} A(x) \phantom{x} dx\end{aligned}
This formula shows that when a given solid, $S$, is composed of slices or cross-sections, $C_x$, $a \leq x \leq b$. In addition, the solid $S$ lies between $C_a$ and $C_b$, which are parallel planes. The area of the cross-sections is defined by the function $A(x)$.
The Cavalieri’s Principle is applied here to calculate the volume of the solid $S$. This is simply an introduction to the concept, so for the rest of the problems shown below, the focus will still be on finding areas and volumes of figures in 2D or 3D.
Example 1
The two solids shown below share the same base area and height as reflected by the parallel plane cutting through each solid. If the rectangular cross-section has a width of $12$ feet and a height of $27\pi$ feet, what is the diameter of the circular base?
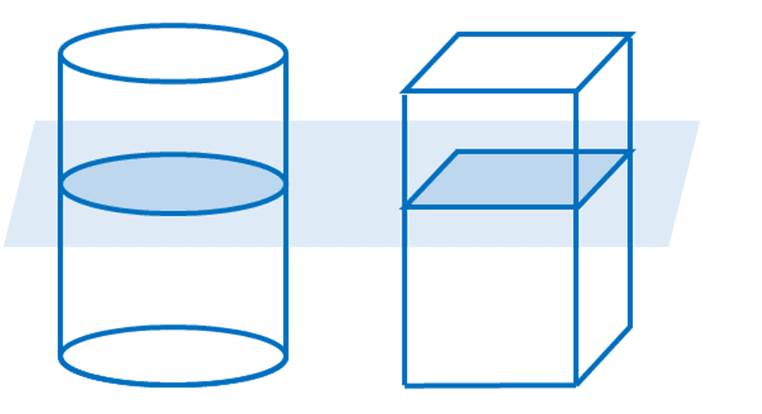
Solution
Both solids can be contained within a pair of parallel planes and the cross-sections divided by the plane are equal, so Cavalieri’s Principle applies. This means that the base areas of the two solids and their heights are equal. First, find the radius of the cylinder’s circular base by equating the bases’ areas.
\begin{aligned}A_{\text{Circle}} &= A_{\text{Rectangle}}\\\pi(r^2) &= l(w)\\\pi r^2 &= 12(27\pi)\\r^2 &= \dfrac{324\pi}{\pi}\\r&= 18\end{aligned}
This means that the radius of the cylinder is $18$ feet long, so its diameter is equal to $2 \times 18 = 36$ feet.
Practice Question
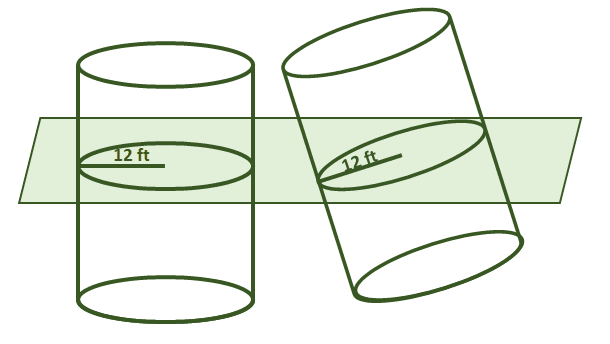
1. True or False: Suppose that the two cylinders shown below share the same heights. Through Cavalieri’s Principle, their volumes are also equal.
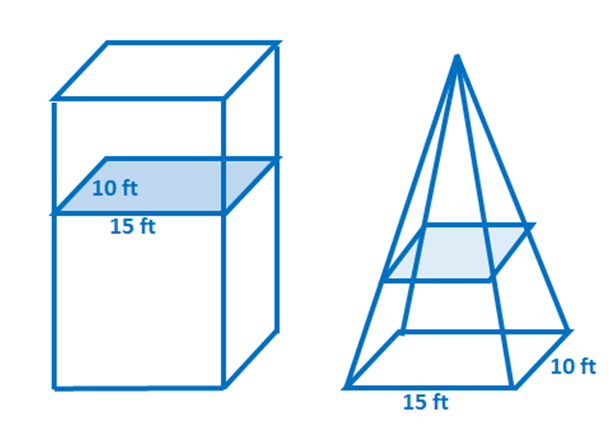
2. True or False: Suppose that the two solids shown below share the same heights. Through Cavalieri’s Principle, their volumes are also equal.
3. What is the volume of the slanted cylinder shown below?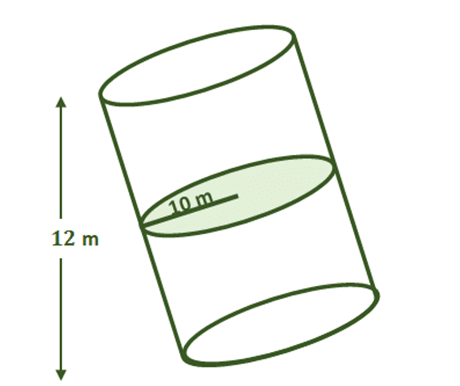
A. $600\pi$ square meters
B. $1200\pi$ square meters
C. $1800\pi$ square meters
D. $2400\pi$ square meters
4. If a rectangular prism with a base length of $40\pi$ shares the same cross-section area and height as the cylinder from the previous problem, what is its base’s width?
A. $15$ meters
B. $20$ meters
C. $30$ meters
D. $45$ meters
Answer Key
1. True
2. False
3. B
4. C
