Chain Rule Integration – Definition and Examples

In this article, we’ll dive deep into the world of ‘Chain Rule Integration,’ illuminating its importance, mechanics, and the various techniques that hinge on its use.

Whether you’re a calculus newbie or an established mathematician looking for a refresher, this comprehensive guide aims to demystify the complexities and equip you with the essential tools to effectively wield the chain rule in your mathematical arsenal.

Definition of Chain Rule Integration

In calculus, the chain rule is predominantly mentioned in the context of differentiation. However, the chain rule can also be applicable to integration via the method known as u-substitution or the substitution method, which is essentially the reverse process of the chain rule in differentiation.

In a nutshell, the chain rule integration, or the substitution method, allows us to transform a complicated integral into a simpler one by substituting a part of the integral (often the inner function of a composite function) with a new variable. This rule is usually expressed as follows:

If u = g(x) is a differentiable function whose range is an interval I and f is continuous on I, then:

∫f(g(x)) * g'(x) dx = ∫f(u) du

Where g'(x) is the derivative of g with respect to x.

By using the substitution method, we can integrate complex expressions that would be difficult or impossible to integrate directly. It is particularly useful when dealing with composite functions, where one function is nested within another.

Figure-1.

Properties

The method of integration by substitution, which is essentially the application of the chain rule Integration, relies on the following properties:

Function Substitution

The central idea behind the chain rule for integration is to substitute a part of the integral (usually the inner function of a composite function) with a new variable. This technique simplifies complex integrals and makes it possible to integrate functions that might otherwise be difficult or impossible to handle.

For example, if we have a function of the form f(g(x)) where g(x) = u, then the integral becomes ∫f(u) * g'(x) dx.

The Differential dx

In the substitution method, we replace a part of the function and its differential with the new variable and its differential. So if u = g(x), then the differential du is equal to g'(x) dx. This replacement allows us to express the original integral entirely in terms of the new variable.

Inverse Substitution

After performing the integration in terms of the new variable, we substitute the original function back into the result to express it in terms of the original variable. This is because the original integral was in terms of x, so the result must also be in terms of x.

Definite Integrals

For definite integrals, we must also change the limits of integration. If the original limits of integration were a and b in terms of x, then the new limits will be g(a) and g(b) in terms of u.

Nested Functions

The chain rule integration is especially useful when dealing with nested or composite functions. This is where we have a function within a function, like sin(x^2) or (e^x)^2. These are usually prime candidates for the substitution method.

Integration Techniques

Sometimes, the chain rule integration is combined with other integration techniques, like integration by parts or partial fractions. This can make it possible to solve even more complex integrals.

Choice of Substitution

The effectiveness of the substitution method often depends on the choice of substitution. It’s often an art as much as a science, and with practice, it becomes easier to identify the best substitution to simplify an integral.

These properties together form the basis of the chain rule integration, a powerful tool for solving a wide range of integrals in calculus.

Ralevent Formulas

In the context of chain rule integration or integration by substitution, there are a few key formulas and principles to keep in mind:

Basic Formula

The fundamental concept of chain rule integration, or integration by substitution, is represented by the formula:

∫f(g(x)) * g'(x) dx = ∫f(u) du

Where u = g(x). The right-hand side of the formula shows the simplified integral after the substitution.

Differential Substitution

An important aspect of substitution is translating the dx term to the new variable. If u = g(x), then the differential of u (du) is calculated as:

du/dx = g'(x)

Which can be rearranged as:

du = g'(x) dx

This du replaces the g'(x) dx in the integral, which assists in transforming the integral into terms of u.

Definite Integrals

In the case of definite integrals, when the limits of the original integral are a and b (with respect to x), after the substitution, the new limits of integration are u(a) and u(b), where u = g(x). So the definite integral becomes:

∫f(g(x)) * g'(x) dx; from a to b = ∫f(u) du; from g(a) to g(b)

Inverse Substitution

After performing the integration, we typically need to substitute back to express the answer in terms of the original variable. If the integral has been calculated to be F(u), where F'(u) = f(u), then the integral in terms of x is given by:

∫f(g(x)) * g'(x) dx = F(u) + C = F(g(x)) + C

Where C is the constant of integration. The result is in the same variable as the original problem.

Computation Process of Chain Rule Integration 

The process of evaluating or computing the chain rule integration, commonly known as u-substitution, is typically as follows:

Choose Your Substitution (u)

Identify a function within the integral that will simplify the integral when substituted out. Often, this will be a function within another function or part of a function whose derivative is also in the integral.

Compute du/dx and dx

Differentiate the function you chose for u with respect to x to get du/dx. Then, solve for dx by rearranging the equation: dx = du / (du/dx).

Make the Substitution

Substitute u into the function and dx into the integral.

Solve the Integral

Now that you have a simpler integral, solve it as you would any other integral. This may require additional techniques, such as integration by parts or trigonometric substitution, for more complex integrals.

Back-Substitute

Once the integral is solved, substitute the original function back in for u to express the solution in terms of the original variable.

Include Constant of Integration

Don’t forget to include the constant of integration, typically denoted as “C,” at the end of your solution. This accounts for the fact that the derivative of a constant is zero and thus doesn’t show up in the original integral.

For Definite Integrals

If you’re solving a definite integral, you’ll need to change the limits of integration to match your u-substitution. When you substitute back in step 5, replace u with its original expression in terms of x, but leave the limits of integration in their substituted form. Then, simply evaluate the antiderivative at the upper limit and subtract the antiderivative evaluated at the lower limit.

This method can dramatically simplify integrals, especially when dealing with composite functions or functions that contain their own derivatives. Practice and familiarity with different types of integrals can help you quickly identify the best function to choose for u in the substitution method.

Exercise 

Example 1

Integrate ∫x * sin(x²) dx

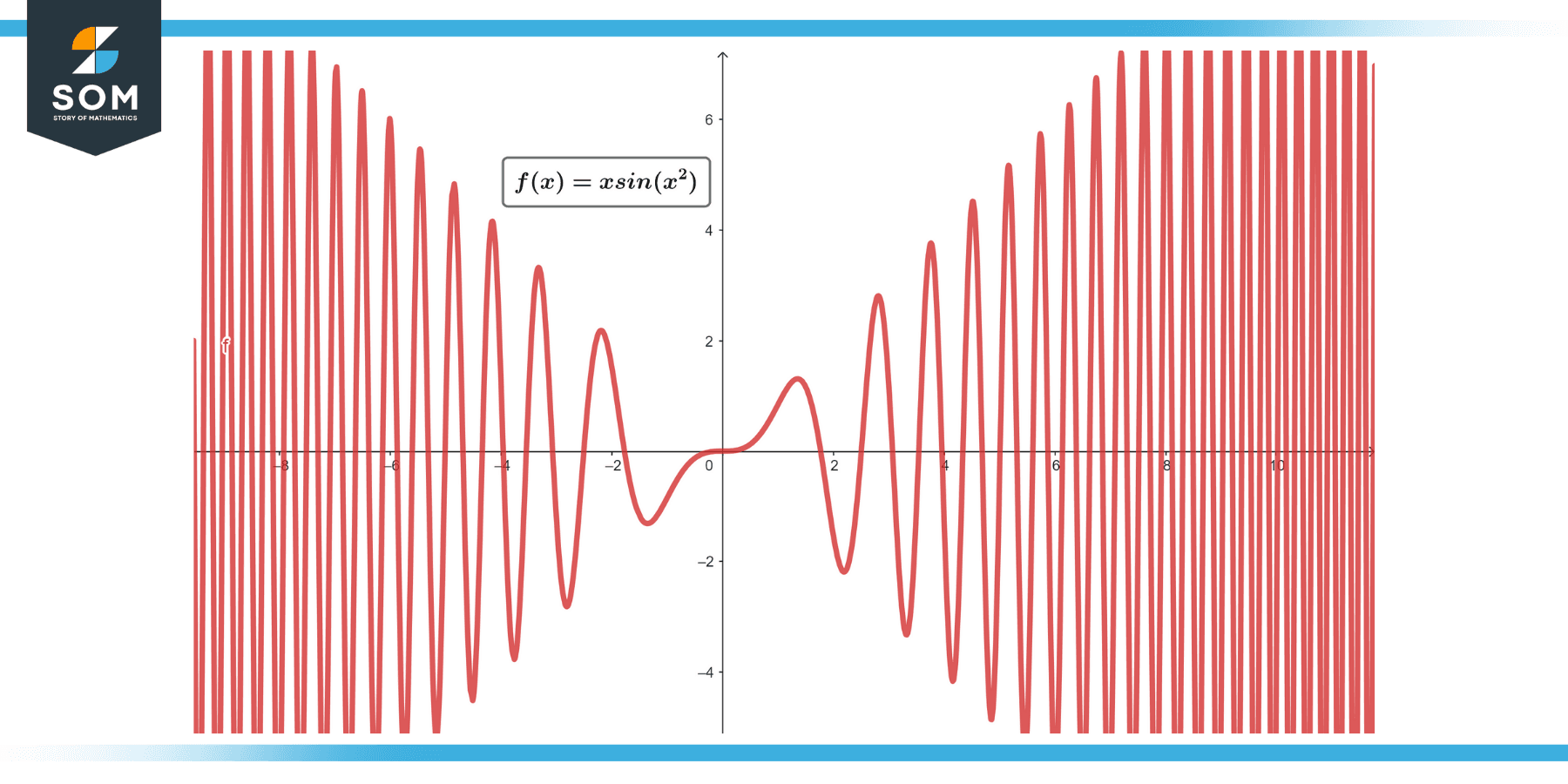
Figure-2.

Solution

Let u = x². Then du/dx = 2x, so dx = du/(2x).

Substitute u and dx into the integral:

∫(1/2) * sin(u) du = -(1/2) * cos(u) + C

= -(1/2) * cos(x²) + C

Example 2

Evaluate ∫(2x) / (1 + x²) dx

Solution

Let u = 1 + x². Then du/dx = 2x, so dx = du/(2x).

Substitute u and dx into the integral:

∫1/u du = ln|u| + C

= ln|1 +x²| + C

Example 3

evaluate ∫$e^(3x)$ dx

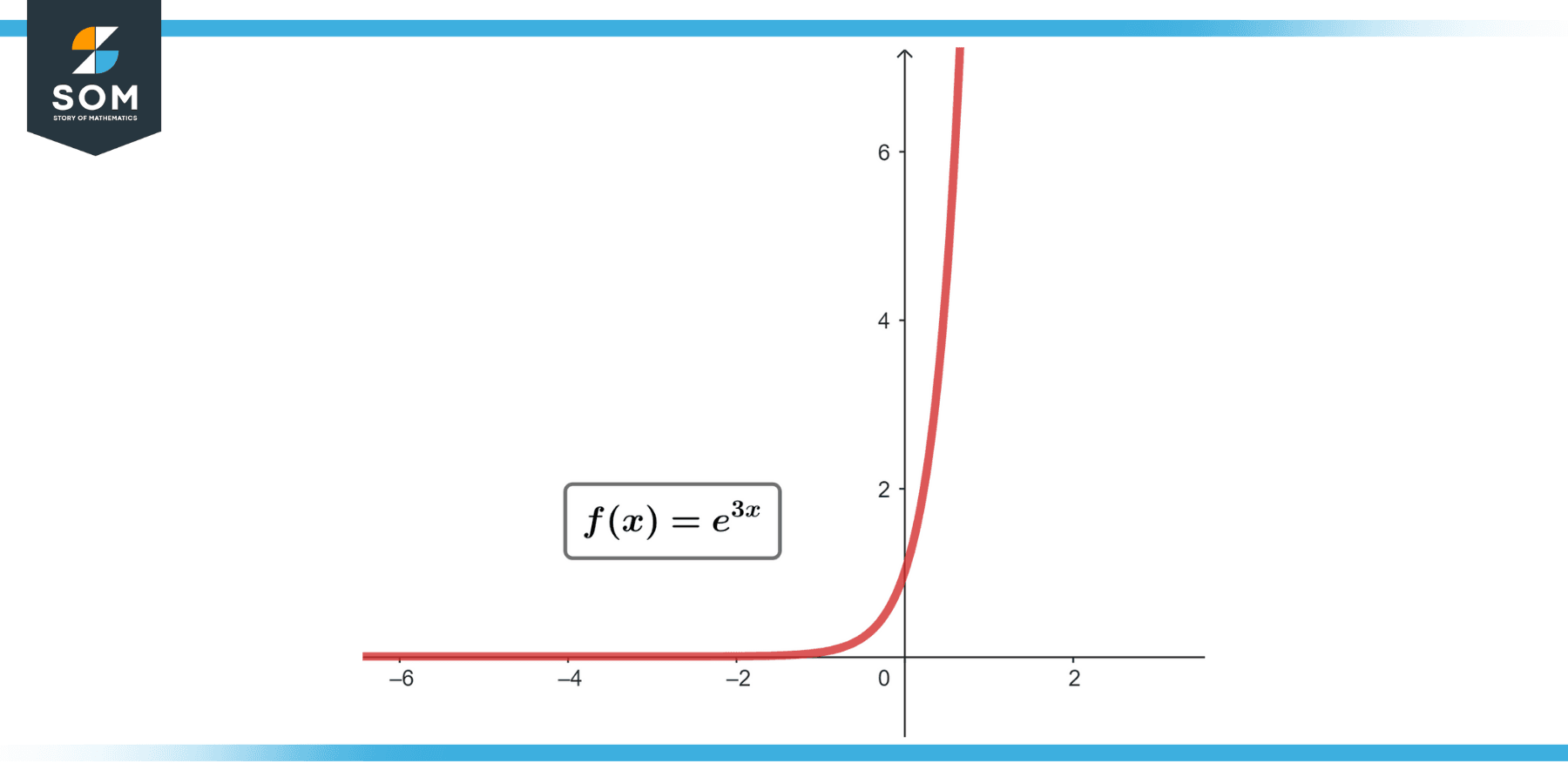
Figure-3.

Solution

Let u = 3 * x. Then du/dx = 3, so dx = du/3.

Substitute u and dx into the integral:

∫(1/3) * $e^u$ du = (1/3) * $e^u$ + C

= (1/3) * $e^{(3x)}$ + C

Example 4:

Evaluate ∫ cos(√(x)) dx

Solution

Let u = √(x), so x = u². Then dx/du = 2u, so dx = 2u du.

Substitute u and dx into the integral:

∫2u * cos(u) du

This is an integration by parts problem. If we let dv = cos(u) du, v = sin(u), and w = 2u, dw = 2 du. Then the integral becomes:

∫w dv = w * v – ∫v dw

∫w dv  = 2u * sin(u) – ∫2sin(u) du

∫w dv  = 2u * sin(u) + 2cos(u) + C

Substitute u back in for √(x):

= 2√(x) * sin(√(x)) + 2cos(√(x)) + C

Example 5:

Evaluate ∫x³ * √(x⁴ + 1) dx

Solution

Let u = x⁴ + 1. Then du/dx = 4x³, so dx = du/(4x³).

Substitute u and dx into the integral:

∫(1/4) *√(u) du = (1/4) * (2/3) * $u^{(3/2)}$ + C

= (1/6) * $(x⁴ + 1)^{(3/2)}$ + C

Example 6:

Evaluate ∫ln(x)/x dx

Solution

Let u = ln(x). Then du/dx = 1/x, so dx = x du.

Substitute u and dx into the integral:

∫u du = (1/2) * u² + C

= (1/2) * (ln(x))² + C

Example 7:

Evaluate ∫sin³(x) cos(x) dx

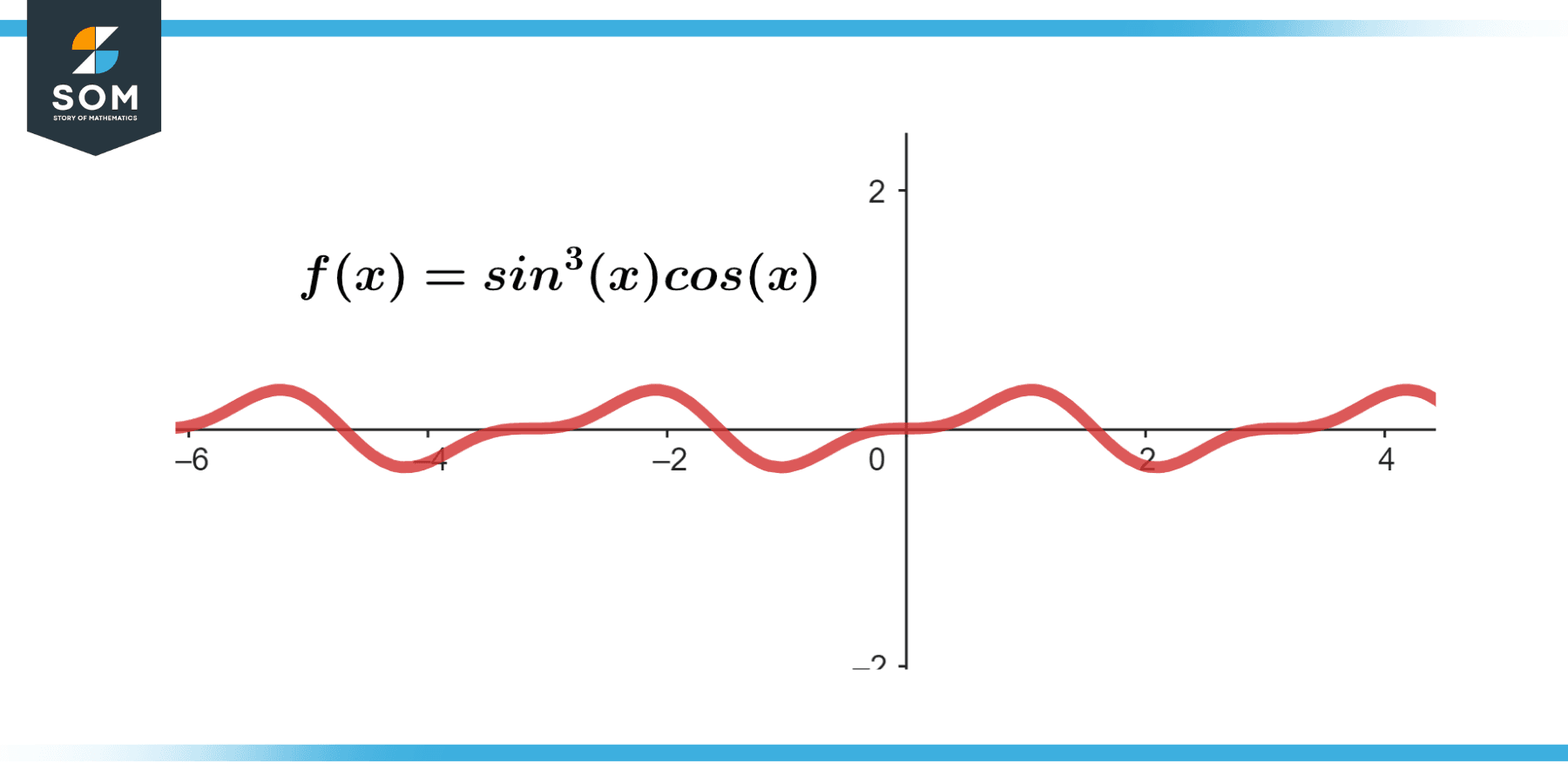
Figure-4.

Solution

Let u = sin(x). Then du/dx = cos(x), so dx = du/cos(x).

Substitute u and dx into the integral:

∫u³ du = (1/4) * u⁴ + C

= (1/4) * sin⁴(x) + C

Applications 

The chain rule integration, or integration by substitution, is a fundamental concept in calculus with a variety of applications in many fields. Here are a few notable examples:

Physics

In physics, chain rule integration is used extensively, especially in the fields of kinematics, quantum mechanics, and electromagnetism. It helps in solving complex integrals that describe physical phenomena like the movement of particles, the interaction of electromagnetic fields, or the behavior of waves.

Engineering

Engineers frequently use calculus, including chain rule integration, to model and solve real-world problems. It can be used to determine the stress and strain distribution in materials, solve electrical circuit problems, calculate fluid flow in pipes, and much more.

Economics and Finance

In economics and finance, integration plays a crucial role in solving problems related to cost, revenue, and profit functions. It can also be used in modeling economic growth, calculating the present value of cash flows, and optimizing resource allocation, among other applications.

Biology

In biology and related fields, chain rule integration is used in modeling population dynamics (like the growth and decay of populations over time), chemical kinetics (like the rate of reactions), and the spread of diseases, to name a few.

Computer Science

Chain rule integration is applied in computer graphics to model continuous change and to render curves and surfaces. It’s also used in machine learning algorithms, particularly in backpropagation in neural networks, which requires both the chain rule for differentiation and its integration counterpart.

Statistics and Probability

In statistics and probability theory, chain rule integration is used to calculate the expected value, variance, and other statistical parameters. It’s also used in the formulation of continuous probability distributions.

All images were created with GeoGebra and MATLAB.