JUMP TO TOPIC

The circumscribed and inscribed circles of triangles play a crucial role in their properties. With their distinct positions and relationships to the triangle’s sides and angles, these circles offer fascinating insights into the nature of triangles and the interplay between their geometric elements.
In this article, we explore the captivating realms of the circumscribed and inscribed circles, uncovering their defining characteristics and the hidden secrets they unveil within the realm of triangles.
Definition of Circumscribed and Inscribed Circles of Triangles
The circumscribed circle passes through all three vertices. It is a unique circle that encompasses the entire triangle within its circumference. The center of the circumscribed circle is equidistant from the three vertices of the triangle, and its radius is known as the circumradius.
On the other hand, the inscribed circle is a circle that is tangent to all three sides of the triangle. The inscribed circle lies entirely within the triangle, with its center coinciding with the intersection point of the angle bisectors of the triangle. The radius of the inscribed circle is referred to as the inradius.
The circumscribed and inscribed circles provide valuable geometric insights and properties of triangles, influencing various aspects such as angle relationships, side lengths, and perimeters. Exploring the characteristics and interplay between these circles sheds light on triangles’ intrinsic geometry and symmetries.
Below we present a generic representation of circumscribed and inscribed circles of triangles in Figure-1.
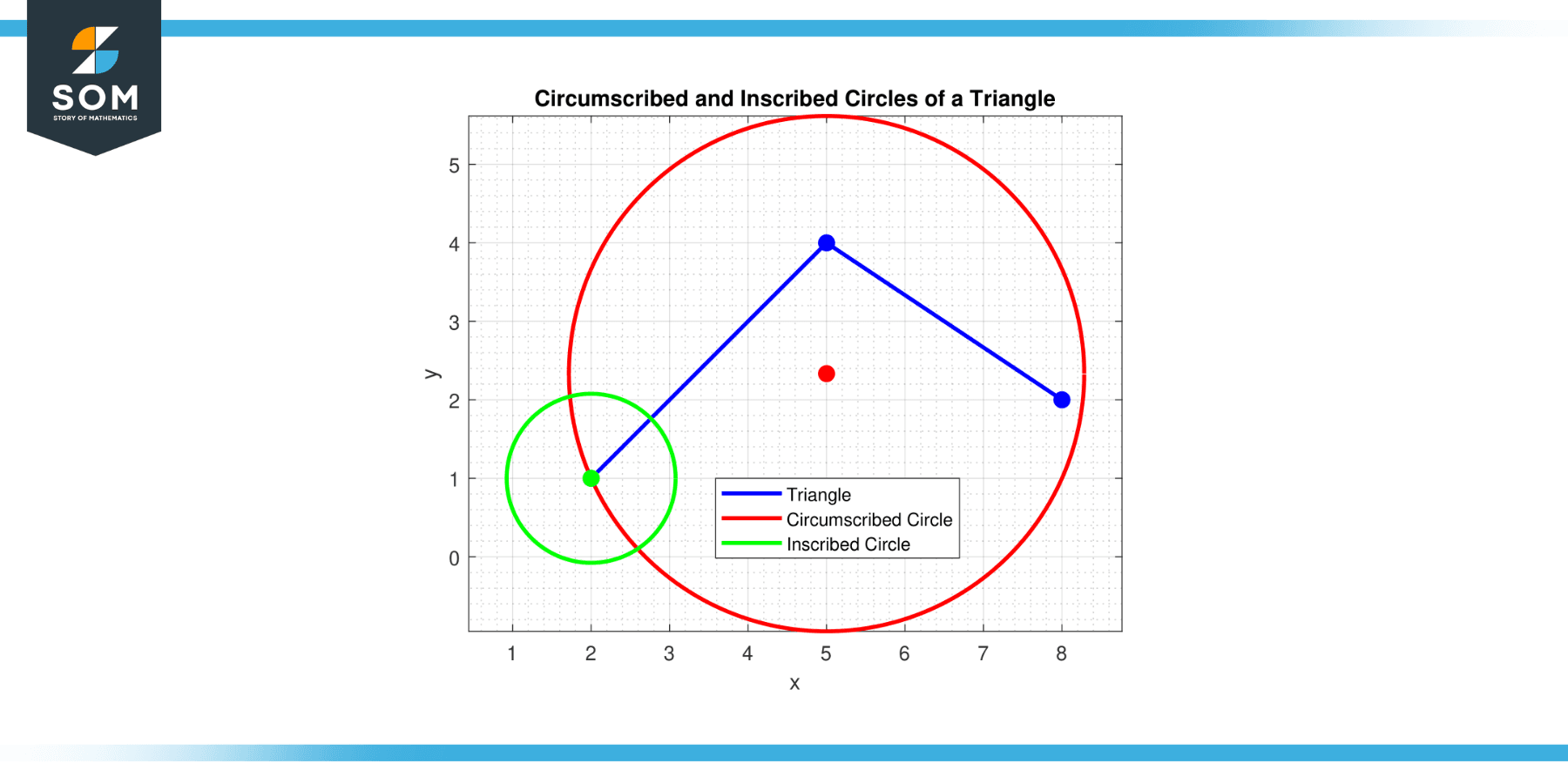
Figure-1.
Properties
Properties of the Circumscribed Circle:
Existence and Uniqueness
Every non-degenerate triangle (a triangle with non-collinear vertices) has a unique circumscribed circle.
Concurrency
The three perpendicular bisectors of the sides of a triangle intersect at a single point, the center of the circumscribed circle. This point is equidistant from the three vertices of the triangle.
Relationship with Angles
The angles subtended by the same arc on the circumcircle are equal. In other words, the measure of an inscribed angle is half the measure of the central angle intercepting the same arc.
Relationship with Sides
The length of a side of the triangle equals the diameter of the circumscribed circle multiplied by the sine of the angle opposite that side.
Circumradius
The radius of the circumscribed circle, known as the circumradius, can be calculated using the formula: R = (abc) / (4Δ), where a, b, and c are the lengths of the triangle’s sides, and Δ represents the area of the triangle.
Maximum Circle
The circumscribed circle has the largest possible radius among all circles drawn around the triangle.
Properties of the Inscribed Circle
Existence and Uniqueness
Every non-degenerate triangle has a unique inscribed circle.
Concurrency
The three angle bisectors of the triangle intersect at a single point, which is the center of the inscribed circle. This point is equidistant from the three sides of the triangle.
Relationship With Angles
The angles formed between the tangent lines from the inscribed circle’s center, and the triangle’s sides are equal.
Relationship With Sides
The radius of the inscribed circle, known as the inradius, can be calculated using the formula: r = Δ / s, where Δ represents the area of the triangle, and s is the semi-perimeter (half the sum of the lengths of the triangle’s sides).
Tangency
The inscribed circle is tangent to each side of the triangle at a single point. These points of tangency divide each side into two segments with lengths proportional to the adjacent sides.
Minimum Circle
The inscribed circle has the smallest possible radius among all circles that can be inscribed within the triangle.
Applications
Trigonometry and Geometry
The properties of circumscribed and inscribed circles are fundamental to trigonometric relationships and geometric constructions involving triangles. They provide a basis for angle measurements, side-length calculations, and establishing geometric proofs.
Surveying and Navigation
The circumscribed circle is applied in the triangulation process in land surveying and navigation. By measuring the angles and distances between known points, the position of an unknown point can be determined by constructing a circumscribed circle around the triangle formed by the known points.
Architecture and Civil Engineering
The circumscribed and inscribed circles are essential in architectural and civil engineering design. For instance, in the construction of circular or polygonal buildings, the circumscribed circle helps determine the ideal size and shape of the structure. The inscribed circle aids in the placement of columns, pillars, or supports within a triangular layout.
Circuits and Electronics
Circumscribed and inscribed circles are employed in circuit analysis and design in electrical engineering. For example, when constructing filters or resonant circuits, the properties of the inscribed circle are used to determine optimal component values and impedance matching.
Computer Graphics and Animation
In computer graphics and animation, the circumscribed and inscribed circles play a role in rendering curved shapes and smooth animations. Algorithms that generate curved surfaces or interpolate points along a curve often utilize the properties of these circles to ensure accuracy and smoothness.
Robotics and Kinematics
The circumscribed and inscribed circles are employed in robotics and kinematics for path planning and motion control. By using the properties of the inscribed circle, robots can navigate tight spaces and calculate optimal trajectories while avoiding collisions.
Pattern Recognition and Image Processing
The properties of circumscribed and inscribed circles are utilized in image processing and pattern recognition algorithms. For instance, in shape recognition, these circles can be used as features to identify and classify objects based on their enclosed shapes.
Exercise
Example 1
Given a triangle with side lengths a = 5 cm, b = 7 cm, and c = 9 cm, find the circumradius (R).
Solution
To find the circumradius, we can use the formula: R = (abc) / (4Δ), where Δ represents the area of the triangle.
First, calculate the area of the triangle using Heron’s formula:
s = (a + b + c) / 2
= (5 + 7 + 9) / 2 = 10 Δ
Δ = √(s(s-a)(s-b)(s-c))
Δ = √(10(10-5)(10-7)(10-9))
Δ = √(1053*1)
Δ = √150
Now, substitute the values into the formula:
R = (abc) / (4Δ)
R = (5 * 7 * 9) / (4 * √150)
R ≈ 6.28 cm
Therefore, the circumradius of the triangle is approximately 6.28 cm.
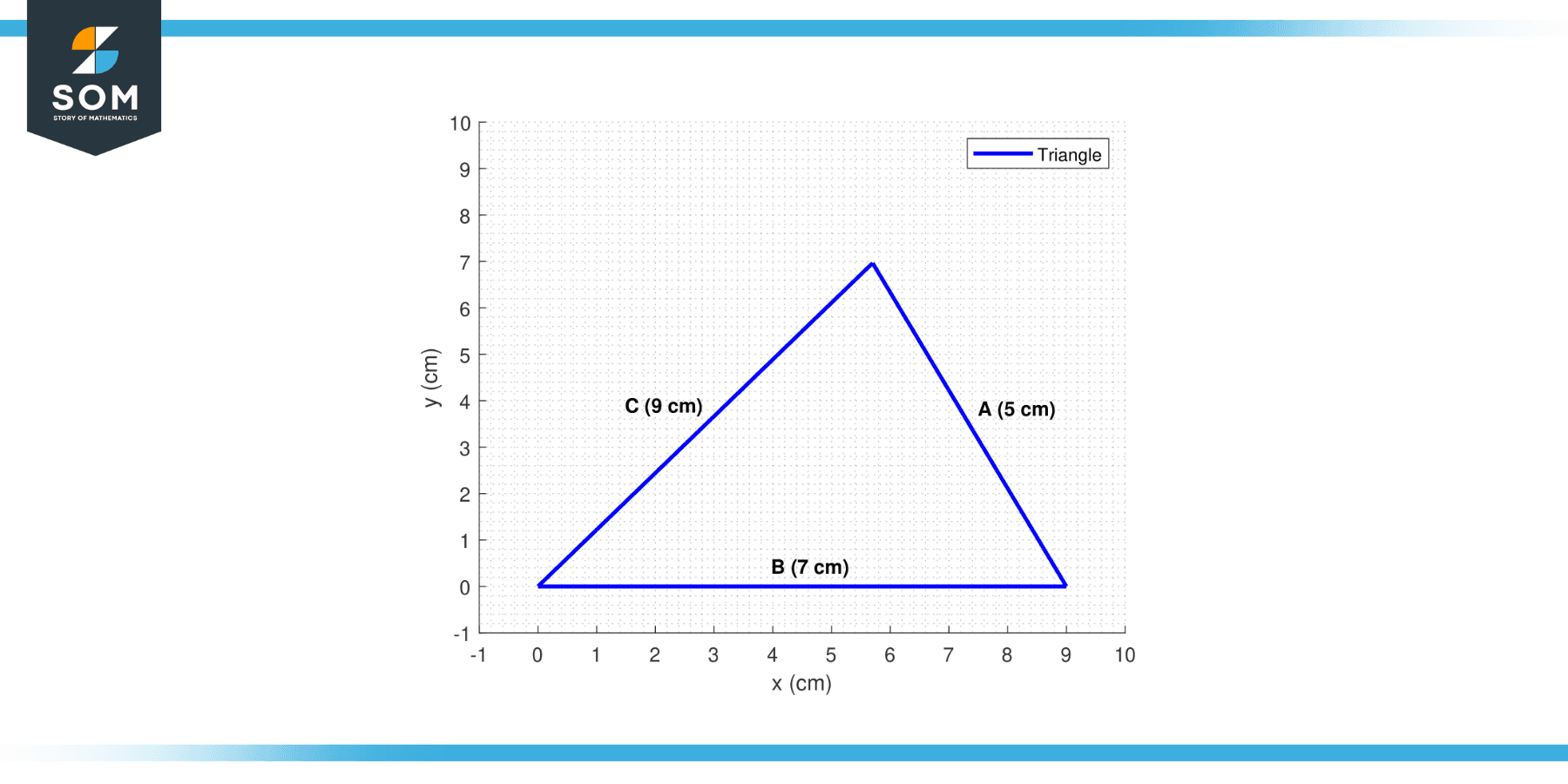
Figure-2.
Example 2
Finding the Inradius of a Triangle Given a triangle with side lengths a = 8 cm, b = 10 cm, and c = 12 cm, find the inradius (r).
Solution
To find the inradius, we can use the formula: r = Δ / s, where Δ represents the area of the triangle and s is the semi-perimeter.
First, calculate the area of the triangle using Heron’s formula:
s = (a + b + c) / 2
s = (8 + 10 + 12) / 2 = 15 Δ
Δ = √(s(s-a)(s-b)(s-c))
Δ = √(15(15-8)(15-10)(15-12))
Δ = √(1575*3)
Δ = √1575
Now, substitute the values into the formula:
r = Δ / s
r = √1575 / 15
r ≈ 7.35 cm
Therefore, the inradius of the triangle is approximately 7.35 cm.
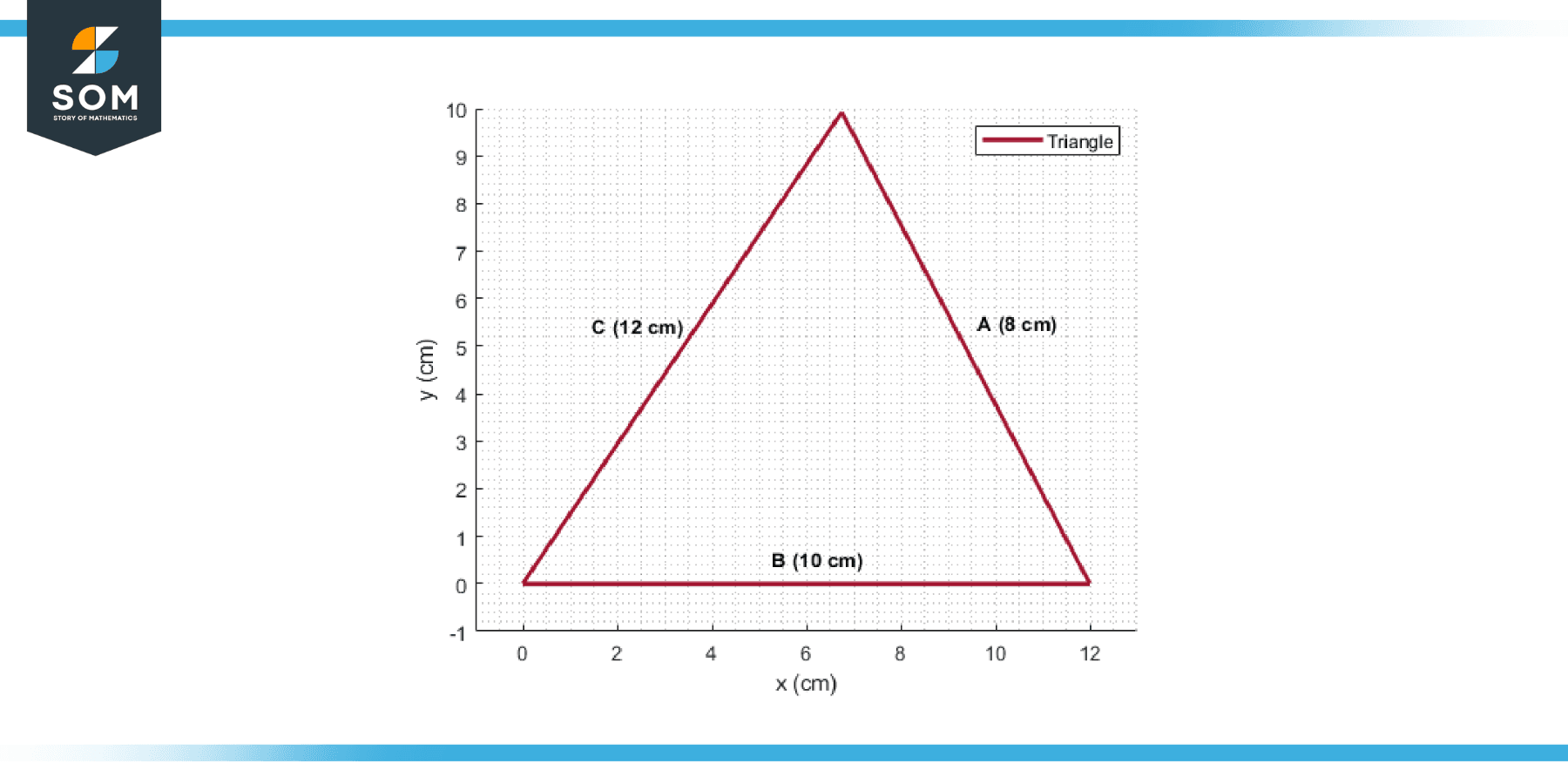
Figure-3.
All images were created with MATLAB.
