JUMP TO TOPIC
This article invites you to explore the cone net, its properties, application, and examples.
Definition of Cone Net
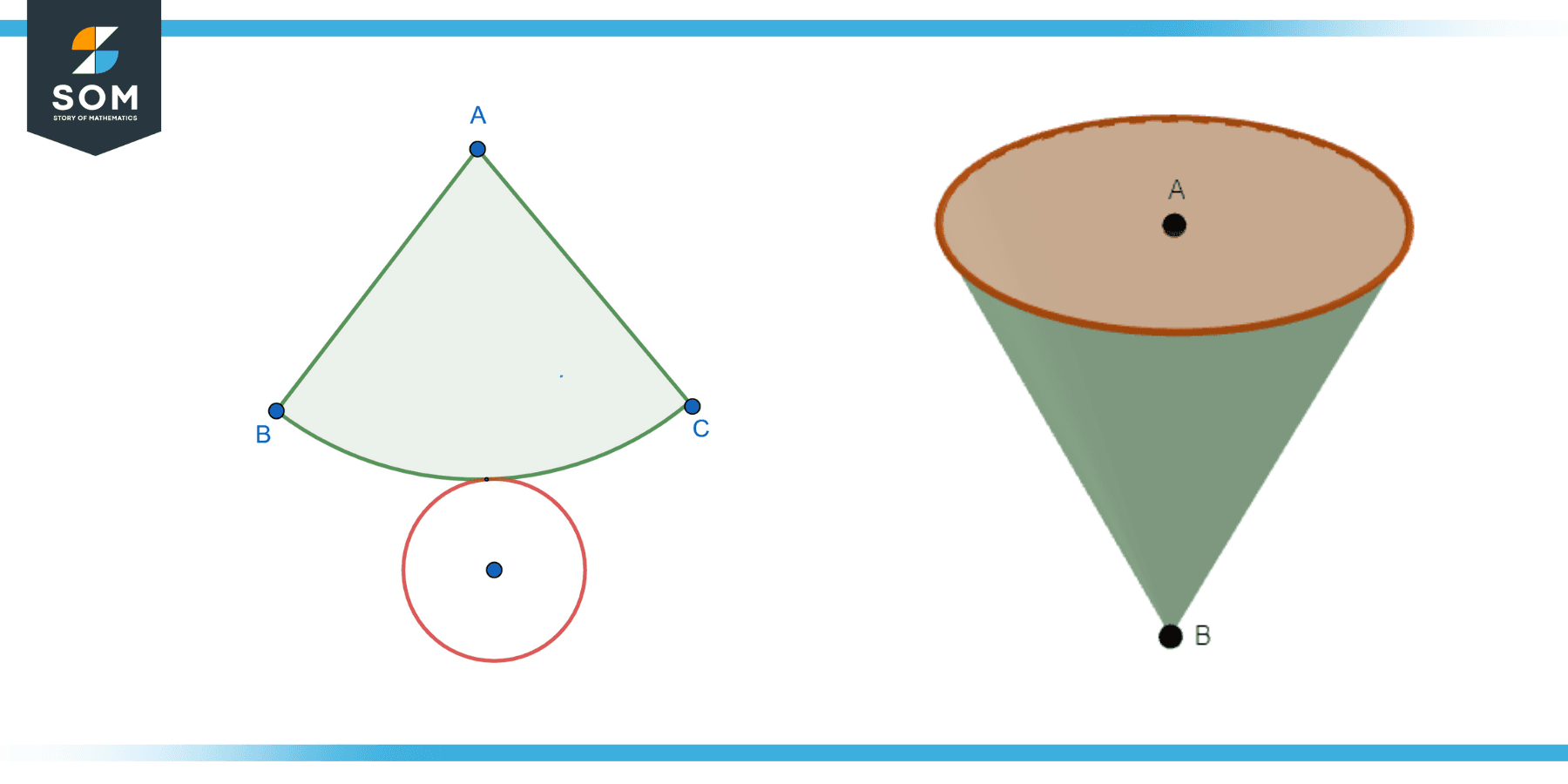
The cone net refers to a two-dimensional pattern that can be folded along its edges to create a three-dimensional shape, in this case, a cone.
The cone net generally consists of a circle (representing the base of the cone) and a sector of a larger circle (representing the lateral or side surface of the cone).
When this net is folded along its edges or boundaries, the sector wraps around to form the curved surface of the cone, and the circle forms the base of the cone.
The point where the sector comes together forms the apex, or tip, of the cone. This is a basic way to understand how two-dimensional shapes can represent and construct three-dimensional objects.
Properties of Cone Net
A net is a two-dimensional figure that can be folded into a three-dimensional object. In the case of a cone, its net has two distinct parts:
Circle
This part forms the base of the cone. The properties of this part of the net include:
- It is a perfect circle, meaning all points on the circle’s edge are equidistant from the center.
- The distance from the center to any point on the edge is the radius of the base of the cone.
- The diameter is the longest distance across the circle, passing through the center. The diameter is twice the length of the radius.
- The total area of the circle can be calculated using the formula πr² (where r is the radius).
- The circle’s perimeter (or circumference) can be calculated using the formula 2πr.
The sector of a Circle
This part forms the cone’s lateral surface area (the side). Its properties include:
- It is a ‘slice’ of a larger circle. The radius of this larger circle is the slant height of the cone.
- The angle of the sector corresponds to the amount of ‘curve’ in the cone. In a right circular cone (a cone where the line from the apex to the center of the base is perpendicular to the base), this angle would be 360 degrees, meaning the sector is a complete circle. This angle would be less than 360 degrees in a non-right circular cone.
- The length of the arc of the sector (the curved edge) is equal to the circumference of the base of the cone. This can be calculated using the formula 2πr, where r is the radius of the base of the cone.
- The area of the sector can be calculated by (θ/360) x πL², where L is the slant height, and θ is the angle of the sector. In the case of a right circular cone, since θ is 360 degrees, the formula simplifies to πL².
When the sector and the circle are folded along their boundaries to form a cone, the circle forms the base, and the sector forms the curved lateral surface of the cone. The point at which the two straight sides of the sector meet forms the cone’s apex.
Exercise
Example 1
The slant height of a cone is 15 cm, and the base has a radius of 9 cm. What is the area of the sector that forms this cone?
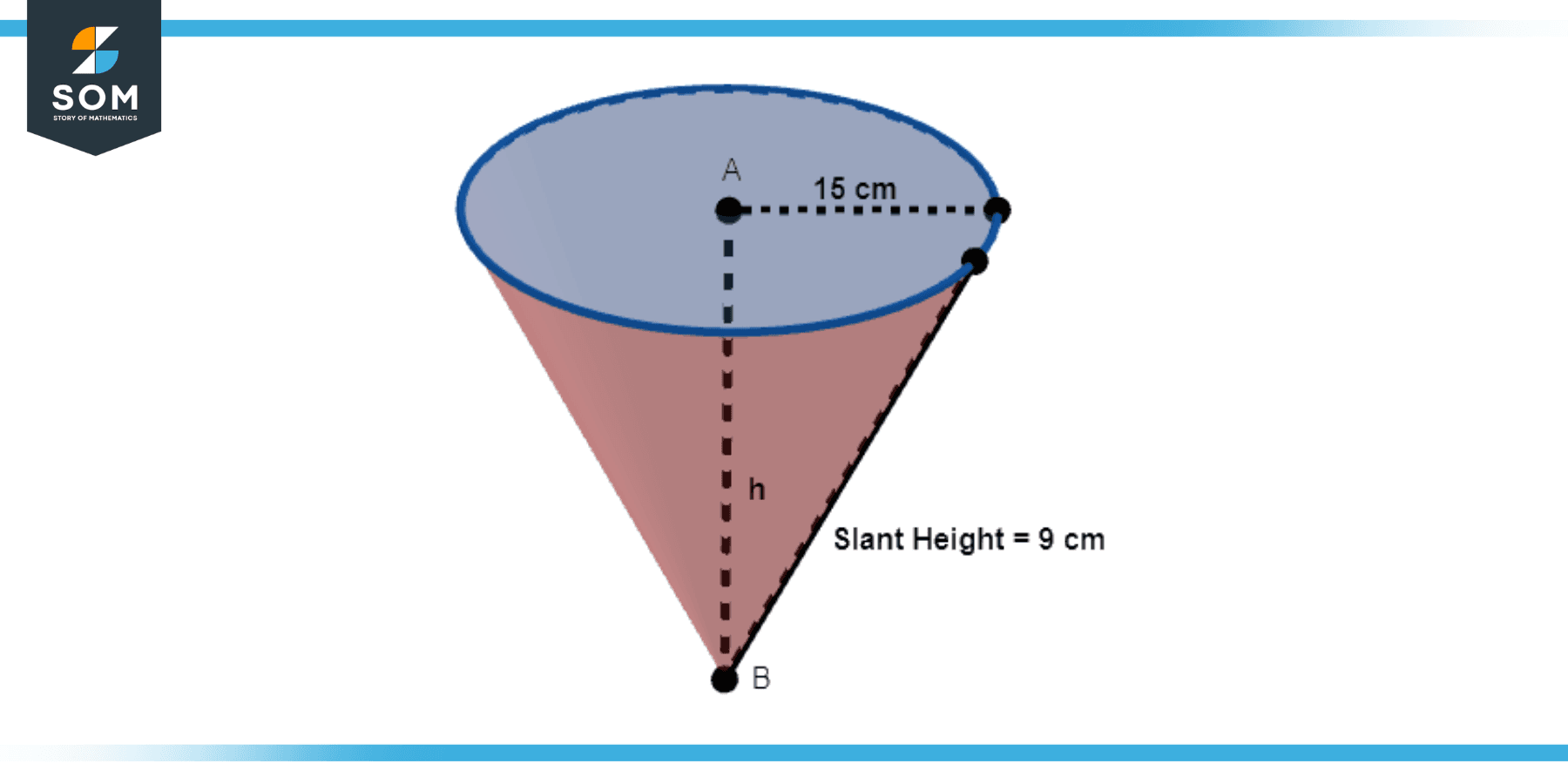
Figure-2.
Solution
The area of the sector is given by:
A = πrL
A = π915
A = 135π cm²
Example 2
A cone has a base circumference of 18π cm and a slant height of 10 cm. What is the radius of the sector used to create this cone?
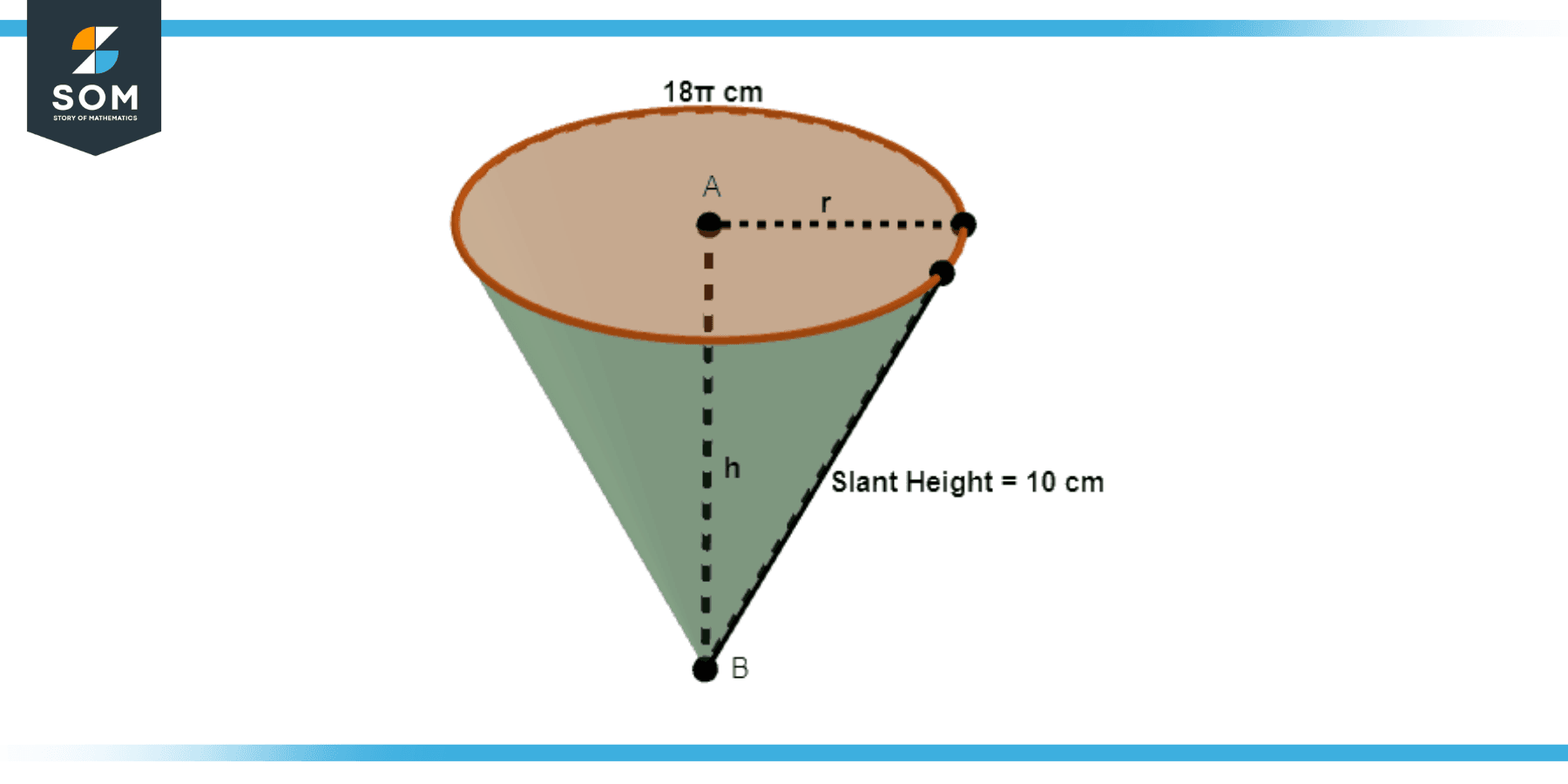
Figure-3.
Solution
The circumference of the base of the cone is equal to the length of the arc of the sector. So, the radius of the sector, which is the slant height of the cone, is 10 cm.
Example 3
A cone has a base area of 25π cm² and a slant height of 10 cm. What is the area of the sector used to create this cone?
Solution
The area of the base of the cone is given by πr², so:
r = √(25π/π)
r = 5 cm
The area of the sector is given by:
A = πrL
A = π510
A = 50π cm²
Applications
The concept of the cone nets, or net of a cone, can be used in various fields. Here are some examples:
Mathematics and Geometry Education
The most direct application of cone nets is in teaching geometry. Understanding the net of a cone can help students visualize and understand three-dimensional shapes. It can also teach mathematical concepts related to surface area and volume.
Engineering and Architecture
Cone nets can be used to design and construct various structures and systems. Architects and engineers often have to work with complex three-dimensional shapes, and understanding the net of those shapes can help with their design process.
Packaging Design
In the field of packaging design, cone nets are used to create packaging that is cone-shaped. For example, the packaging for certain types of food items like ice cream cones or certain types of gift boxes.
Arts and Crafts
Cone nets can be used in a variety of arts and crafts projects. They can be used to create three-dimensional shapes from paper or other materials.
3D Modeling and Printing
Understanding how to create a cone net can be useful in 3D modeling software, where you might need to create a cone-shaped object. Similarly, when 3D printing, understanding the net of a cone can be useful for deconstructing complex shapes into printable components.
Astronomy and Physics
Cone nets can also be used in certain fields of science. For example, in astronomy, cone-shaped zones are often used to represent fields of view.
All images were created with GeoGebra.

