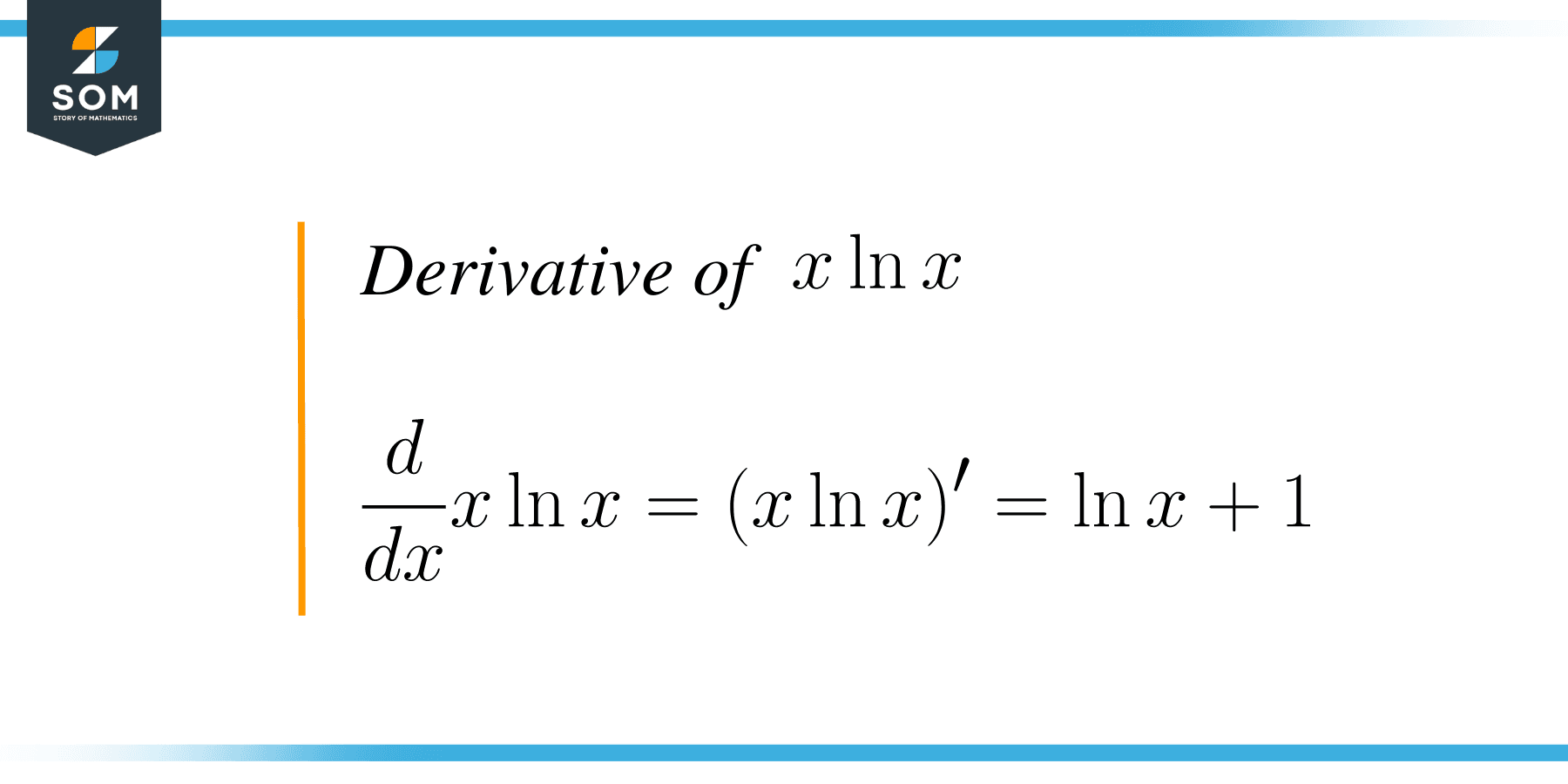What Is the Derivative of xln x?

The derivative of $x\ln x $ is $\ln x+1$. In mathematics, a derivative is the rate of change of a function with respect to a parameter. Derivatives are essential for solving differential equations and calculus problems. Throughout this complete guide, we will go over the steps for calculating the derivative of $x\ln x$.

What Is the Derivative of x ln x?

The derivative of $x\ln x $ is $\ln x+1$. The product rule can be used to determine the derivative of $x\ln x $ concerning $x$. The product rule is a calculus methodology that is used to work out the derivatives of the products of two or more functions.

Let $w$ and $z$ be two functions of $x$. The product rule for $w$ and $z$ can be written as:

$(wz)’=wz’+zw’$ or $\dfrac{d}{dx}(wz)=w\dfrac{dz}{dx}+z\dfrac{dw}{dx}$.

When the functions are multiplied by each other and the derivative of their product is taken, then this derivative will be equal to the sum of the product of the first function with the derivative of the second function and the product of the second function with the derivative of the first function, according to the equation above. If more than two functions are present, the product rule can be utilized there as well. Each function’s derivative is multiplied by the other two functions and summed up together.

The first step in finding the derivative of $x\ln x $ is to suppose that $y=x\ln x$ for simplification. Next, take the derivate of $y$ with respect to $x$ as: $\dfrac{dy}{dx}=\dfrac{d}{dx}(x\ln x)$. The derivative of $y$ can be denoted by $y’$. Moreover, it is well known that $\dfrac{dx}{dx}=1$ and $\dfrac{d(\ln x)}{dx}=\dfrac{1}{x}$.

Steps Involved in the Derivative of x ln x

The above results used in the product rule will result in the derivative of $x\ln x$ with respect to $x$. The steps involved in this case are:

Step 1: Rewrite the equation as:

$y=x\ln x$

Step 2: Take the derivative:

$\dfrac{dy}{dx}=\dfrac{d}{dx}(x\ln x)$

Step 3: Apply the product rule:

$y’=x\dfrac{d}{dx}(\ln x)+\ln x\dfrac{d}{dx}(x)$

Step 4: Use the derived forms of $x$ and $\ln x$:

$y’=x\cdot \dfrac{1}{x}+\ln x\cdot 1$

Step 5: The final answer:

$y’=\ln x+1$

How To Find the Derivative of x ln x by First Principle

By definition, a derivative is the use of algebra to obtain a general definition for the slope of a curve. It is additionally referred to as the delta technique. The derivative expresses the instantaneous rate of change and is equivalent to:

$f'(x)=\lim\limits_{h\to 0}\dfrac{f(x+h)-f(x)}{h}$

To find the derivative of $x\ln x$ using the First Principle, assume that $f(x)=x\ln x$ and so that $f(x+h)=(x+h)\ln(x+h)$. By replacing these values in the derivative definition, we get:

$f'(x)=\lim\limits_{h\to 0}\dfrac{(x+h)\ln(x+h)-x\ln x}{h}$

Rearrange the denominators as follows:

$f'(x)=\lim\limits_{h\to 0}\dfrac{x\ln(x+h)-x\ln x+h\ln(x+h)}{h}$

$f'(x)=\lim\limits_{h\to 0}\dfrac{x[\ln(x+h)-\ln x] + h\ln(x+h)}{h}$

By the property of logarithms, $\ln a -\ln b=\ln\left(\dfrac{a}{b}\right)$. Utilizing this property in the preceding definition, we obtain:

$f'(x)=\lim\limits_{h\to 0}\dfrac{x\ln\left(\dfrac{x+h}{x}\right)+h\ln(x+h)}{h}$
$f'(x)=\lim\limits_{h\to 0}\dfrac{x\ln\left(1+\dfrac{h}{x}\right)}{h}+\ln(x+h)$

Let us suppose that $\dfrac{h}{x}=u$, so that, $h=ux$. The change in limits can take place as $h\to 0$, $u\to 0$. Replacing these numbers in the above formula, we get:

$f'(x)=\lim\limits_{u\to 0}\dfrac{x\ln\left(1+u\right)}{ux}+\ln(x+ux)$

The above expression needs to be simplified in the following way:

$f'(x)=\lim\limits_{u\to 0}\left[\dfrac{\ln\left(1+u\right)}{u}+\ln(x(1+u))\right]$

Now to proceed further, use the logarithmic property $\ln(ab)=\ln a+\ln b$.

$f'(x)=\lim\limits_{u\to 0}\left[\dfrac{\ln\left(1+u\right)}{u}+\ln x+\ln(1+u)\right]$

$f'(x)=\lim\limits_{u\to 0}\left[\dfrac{1}{u}\ln(1+u)+\ln x+\ln(1+u)\right]$

Next, make use of the property $a\ln b=\ln b^a$.

$f'(x)=\lim\limits_{u\to 0}\left[\ln(1+u)^{\frac{1}{u}}+\ln x+\ln(1+u)\right]$

The limit can be applied to terms containing $u$ because $x$ is independent of the variable of the limit.

$f'(x)=\ln\lim\limits_{u\to 0}(1+u)^{\frac{1}{u}}+\ln x+\ln\lim\limits_{u\to 0}(1+u)$

Using the limit definition $\lim\limits_{u\to 0}(1+u)^{\frac{1}{u}}=e$ on first term, we get:

$f'(x)=\ln e+\ln x+\ln(1+0)$

It is well known that $\ln(1)=0$ and $\ln e=1$, so we have:

$f'(x)= \ln x + 1 $

Hence, the derivative of $x\ln x$ using the first principle is $ \ln x + 1$.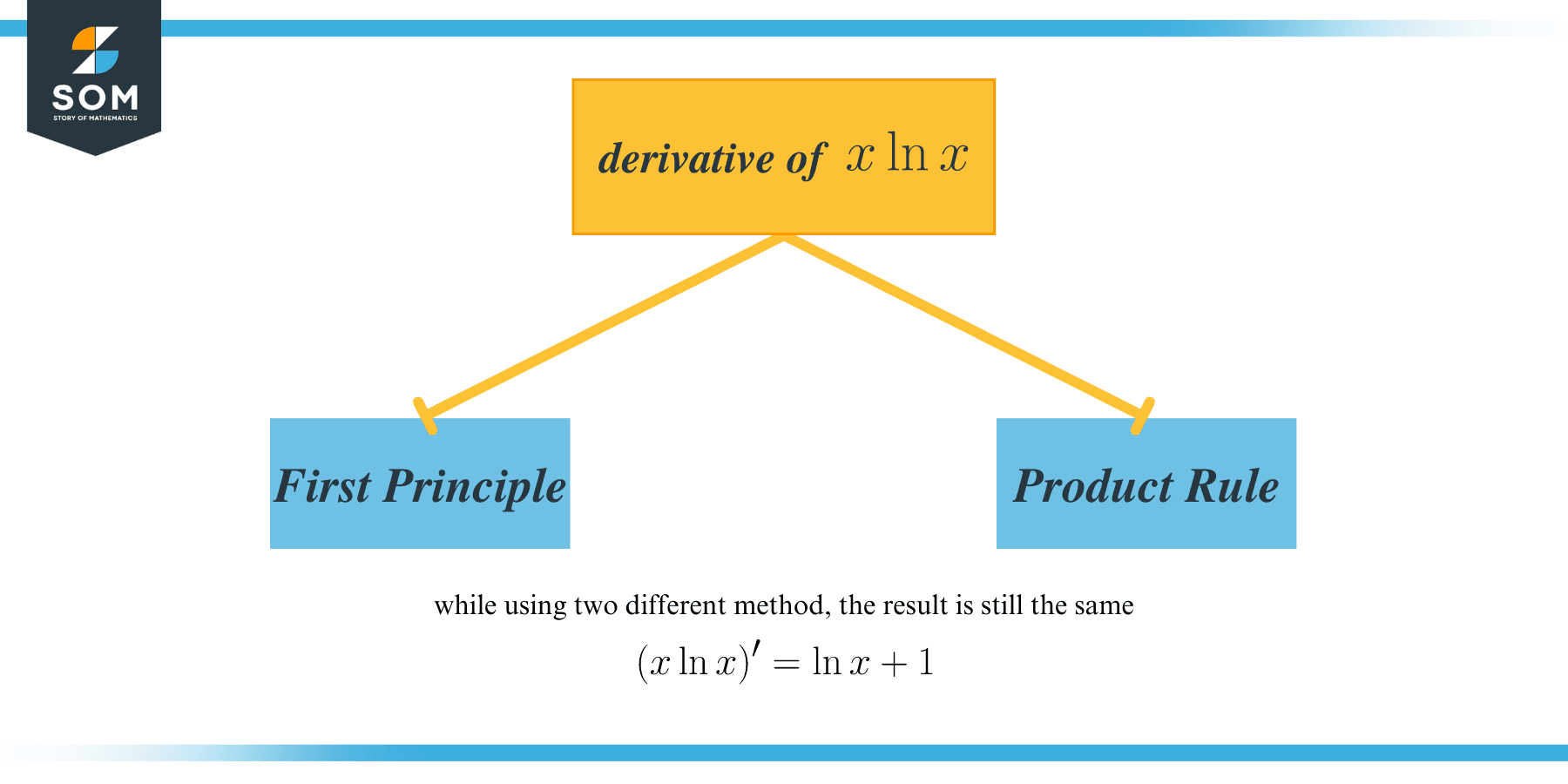

Why x log x and x ln x Do Not Have the Same Derivative

The reason behind the functions $x\log x$ and $x\ln x$ having dissimilar derivatives is because of the different definitions of the $\log$ and $\ln$. The distinction between $\log$ and $\ln$ is that $\log$ is for the base $10$ and $\ln$ is for base $e$. The natural logarithm can be identified as the power to which we can raise the base $e$, also known as its log number, where $e$ is referred to as an exponential function.

On the other hand, $\log x$ generally refers to the logarithm of the base $10$; it could also be written as $\log_{10}x$. It tells you up to which power you need to raise $10$ to get the number $x$. This is known as a common logarithm. The common logarithm’s exponent form is $10^x =y$.

What Is the Derivative of x log x?

Unlike the $x\ln x$, the derivative of $x\log x$ is $\log(ex)$. Let us figure out its derivative using some interesting steps. Initially, assuming that $y=x\log x$ is the first step. As the next step, use the product rule as follows:

$y’=x\dfrac{d}{dx}(\log x)+\log x\dfrac{d}{dx}(x)$

Now it is well known that the derivative of $x$ with respect to $x$ is $1$. To find the derivative of $\log x,$ use the change of base law first:

$\dfrac{d}{dx}(\log x)=\dfrac{d}{dx}\left(\dfrac{\log x}{\log 10}\right)=\dfrac{d}{dx}\left(\dfrac{\ln x}{\ln 10}\right)=\dfrac{1}{\log 10}\dfrac{d}{dx}(\ln x)$

Since we have obtained the derivative of $\ln x$ as $\dfrac{1}{x}$, so $\dfrac{d}{dx}(\log x)=\dfrac{1}{x\ln 10}$. As a next step, we will substitute these derivatives into the product rule formula which will then have the form:

$y’=\dfrac{x}{x\ln 10}+\log x$

$y’=\dfrac{1}{\ln 10}+\log x$

$y’=\dfrac{\log e}{\log 10}+\log x$

Use the fact that $\log 10=1$ to have $y’=\log e+\log x$. As the last step, you need to use the logarithmic property that is $\log a+\log b=\log(ab)$. Finally, you will get the result as: $y’=\log(ex)$ or $\dfrac{d}{dx}(x\log x)=\log(ex)$. In this way, you can show that the derivatives of $x\log x$ and $x\ln x$ are different.

The Second Derivative of x ln x

The second-order derivative can simply be defined as the derivative of a function’s first-order derivative.  The $n$th order derivative of any given function can be found in the same way as the second derivative. When the derivative of a polynomial function is taken up to a certain degree, it becomes zero. Functions with negative powers, such as $x^{-1},x^{-2},\cdots$, on the other hand, do not vanish when the higher-order derivatives are taken.

You can find the second derivative of $x\ln x$ by taking the derivative of $\ln x + 1$. Since previously it was obtained that $y’=\ln x+1$, we can denote the second derivative by $\dfrac{d^2}{dx^2}{(y)}=y”$. Also, there are two separate terms due to which you do not have to use the product rule. The derivative will be directly applied to each term as follows:

$\dfrac{d}{dx}(y’)=\dfrac{d}{dx}(\ln x)+\dfrac{d}{dx}(1)$

The derivative of $\ln x=\dfrac{1}{x}$ and the derivative of a constant is always zero, therefore, the second derivative of $x\ln x$ is:

$y”=\dfrac{1}{x}+0$ or $y”=\dfrac{1}{x}$

From the second derivative, you can see that this derivative will not vanish as we take the higher-order derivatives of $x\ln x$. The $n$th derivative of $x\ln x$ will result in higher powers of $x$ in the denominator.

Conclusion

We’ve covered a lot of ground in our search for the derivative of $x\ln x$, so to ensure that you can easily find the derivative of the functions involving natural logarithm, let us summarize the guide:

• The derivative of $x\ln x$ is $\ln x+1$.
• Finding the derivative of this function requires the application of the product rule.
• You will get the same result regardless of the method used in finding the derivative of $x\ln x$.
• The derivatives of $x\log x$ and $x\ln x$ are not the same.
• The higher order derivatives of $x\ln x$ will result in the higher powers of $x$ in the denominator.

The derivative of the functions involving the product of two terms having the independent variable can be found using the product rule. Other rules, such as the power rule, sum and difference rule, quotient rule, and chain rule are present to make the differentiation easier. So search for some interesting functions involving natural and common logarithms or the product of two terms having the independent variable to have a nice command on the derivatives using the product rule.