JUMP TO TOPIC
This article explores the enthralling world of function addition, diving into its definition, properties, and varied applications.
Whether you’re a math enthusiast seeking to enrich your understanding or a curious reader venturing into the captivating depths of calculus, this exploration of function sums aims to unravel its complexity, shedding light on how this concept helps shape our understanding of the mathematical world and its practical implications.
Defining Sum of Functions
In mathematics, the sum of two functions is a new function that results from adding the outputs of the two functions for each corresponding input.
If we have two functions, f(x) and g(x), the sum of these functions, often denoted as (f + g)(x), is defined as:
(f + g)(x) = f(x) + g(x)
This means for every input x into your new function (f + g)(x), you calculate the value of f(x) and g(x) separately and then add those two results together.
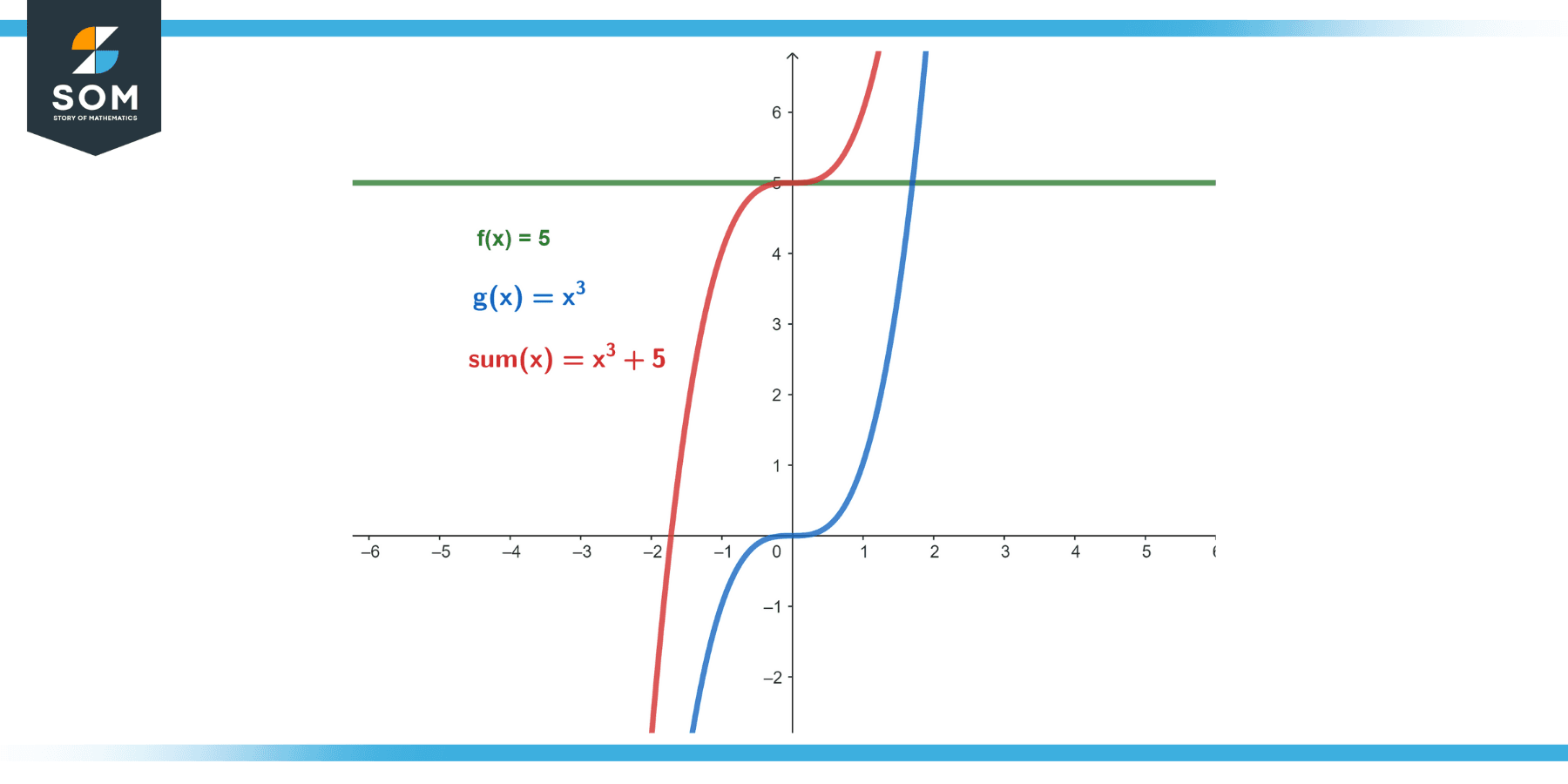
Figure-1.
It’s important to note that the sum of functions concept extends beyond just two functions. We can define the sum of any number of functions similarly.
Properties
The sum of functions, as a basic operation in mathematics, possesses certain key properties that are rooted in the principles of function theory and algebra. Here are the primary properties:
Commutativity
The sum of two functions is commutative, meaning the order in which the functions are added does not change the result. If f(x) and g(x) are two functions, then (f + g)(x) = (g + f)(x).
Associativity
The sum of functions is also associative. This means that if f(x), g(x), and h(x) are three functions, then ((f + g) + h)(x) = (f + (g + h))(x).
Identity
The zero function, denoted as 0, where 0(x) = 0 for all x in the domain, acts as the identity for function addition. If f(x) is a function, then (f + 0)(x) = f(x).
Inverse
Every function f(x) has an additive inverse -f(x), such that when the function and its inverse are added, the result is the zero function: (f + (-f))(x) = 0(x).
Distributivity
The sum of functions also has distributivity property over scalar multiplication (real or complex numbers). If f(x) and g(x) are functions and c is a scalar, then c * (f + g)(x) = (c*f)(x) + (c*g)(x).
Distributivity over Function Multiplication
Function addition is also distributive over function multiplication. This means that (f * (g + h))(x) = (f*g)(x) + (f*h)(x).
Exercise
Example 1
Sum the following two functions:
f(x) = x²
g(x) = x + 3
Solution
The sum of these two functions is:
(f + g)(x) = f(x) + g(x) = x² + x + 3
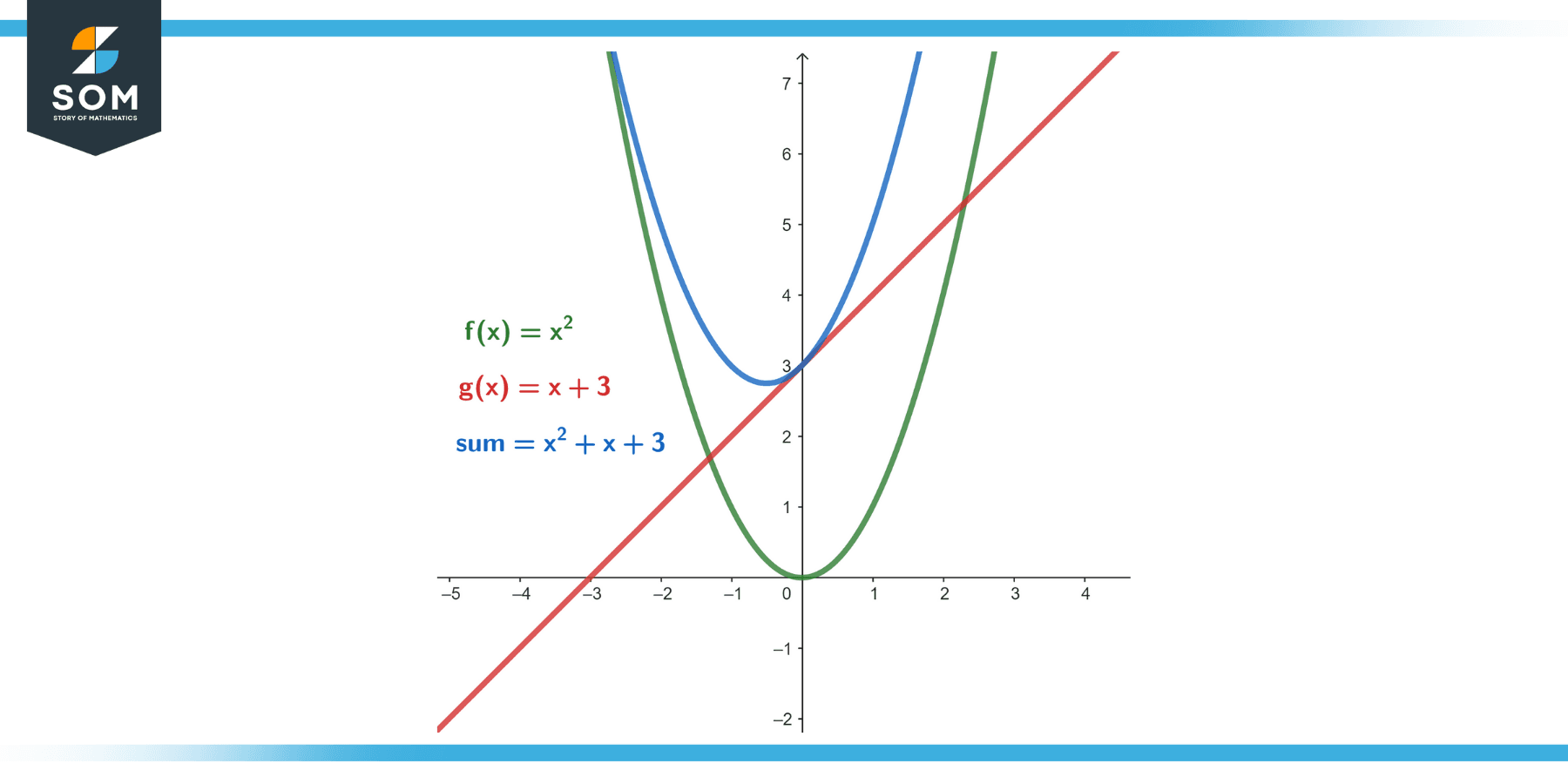
Figure-2.
Example 2
Sum the following two polynomial functions:
f(x) = 3x³ – 2x + 1
g(x) = 4x² + 3x – 1
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = 3x³ + 4x² + x
Example 3
Sum the following two trigonometric functions:
f(x) = sin(x)
g(x) = cos(x)
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = sin(x) + cos(x)
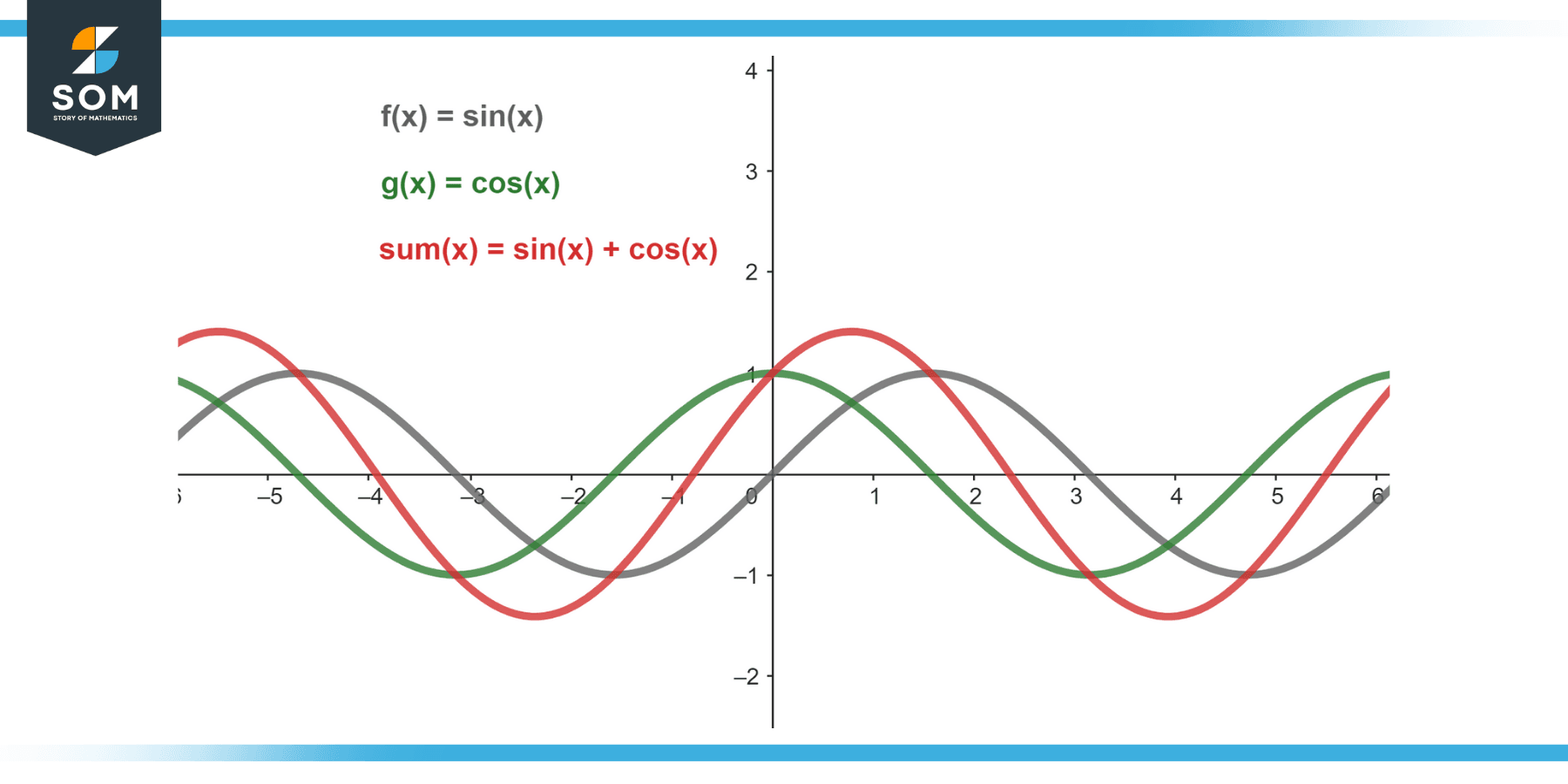
Figure-3.
Example 4
Sum the following linear function and a quadratic function:
f(x) = 2x + 1
g(x) = x² – 3
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = x² + 2x – 2
Example 5
Sum the following exponential function and a logarithmic function:
f(x) = eˣ
g(x) = ln(x) (Natural logarithm)
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = eˣ + ln(x)
Example 6
Sum the following two rational functions:
f(x) = 1/x
g(x) = 1/(x²)
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = 1/x + 1/(x²)
Example 7
Sum the following two radical functions:
f(x) = √x
g(x) = √(2x)
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = √x + √(2x)
Example 8
Suppose we have a function that is constant and a cubic function:
f(x) = 5
g(x) = x³
Solution
The sum of these functions is:
(f + g)(x) = f(x) + g(x) = x³ + 5
Applications
The sum of functions concept, which lies at the heart of many mathematical operations, finds use in various fields due to its inherent utility. Here are some notable applications:
Physics
In physics, multiple forces often act on an object simultaneously. Each of these forces can be represented as a function of position, time, or other variables, and the net force acting on the object is the sum of these individual force functions. The concept of the sum of functions also plays a crucial role in wave superposition, where multiple waves combine to form a resultant wave.
Engineering
Engineers often need to analyze the combined effect of different factors. For example, in electrical engineering, the total current or voltage in a circuit can be the sum of the currents or voltages from multiple sources, represented as functions of time.
Economics
In economics, a firm’s total cost function is often the sum of different cost functions such as fixed costs, variable costs, etc. Similarly, a market demand function can be represented as the sum of individual demand functions.
Computer Science
In machine learning and artificial intelligence, an ensemble of models (like a neural network or a decision forest) can be seen as the sum of simpler functions or models. Each model makes a prediction (a function of the input), and these predictions are combined (often by summing) to make a final prediction.
Statistics
In statistics, the concept of the sum of functions is employed when dealing with the probability density function of the sum of independent random variables.
Medicine
In medicine, different risk factors can contribute to the overall disease risk. Each risk factor can be modeled as a function of various health metrics (like age, BMI, cholesterol level, etc.), and the overall risk can be modeled as the sum of these individual risk functions.
These examples illustrate that function addition is ubiquitous and immensely useful in diverse scientific fields. By understanding and applying this concept, one can analyze complex systems piecewise, breaking them down into simpler components that can be individually understood and combined.
All images were created with GeoGebra.

