JUMP TO TOPIC
The curvature formula an expressed equation gives us a way to quantitatively understand how shapes bend and reveal their inherent properties.
In this article, we will dive into the intricacies of the curvature formula examine how it was derived, and highlight its importance in disciplines such, as architecture and theoretical physics.
Definition of the Curvature Formula
Mathematically, the curvature formula (k) of curve r(t) = (x(t), y(t)) at a point (x0, y0) is defined as:
k = (x'(t) y”(t) – y'(t) x”(t)) / ( $x'(t)^2 + y'(t)^2)^{3/2}$)
In this formula, x'(t) and y'(t) represent the first derivatives of x and y with respect to t, and x”(t) and y”(t) represent their second derivatives.
In geometry and calculus, the curvature of a curve at a given point is defined as, how much the curve deviates from being a straight line at that point.
The curvature essentially measures the rate of change of the tangent angle to the curve, giving a sense of how sharply the curve bends at any given point. For instance, a straight line has a curvature of zero, as it does not bend, whereas circles have a constant curvature.
The curvature formula is used to measure the degree of bending at a point on a curve. It does this by considering the rates at which the curve’s derivatives change and their magnitudes.
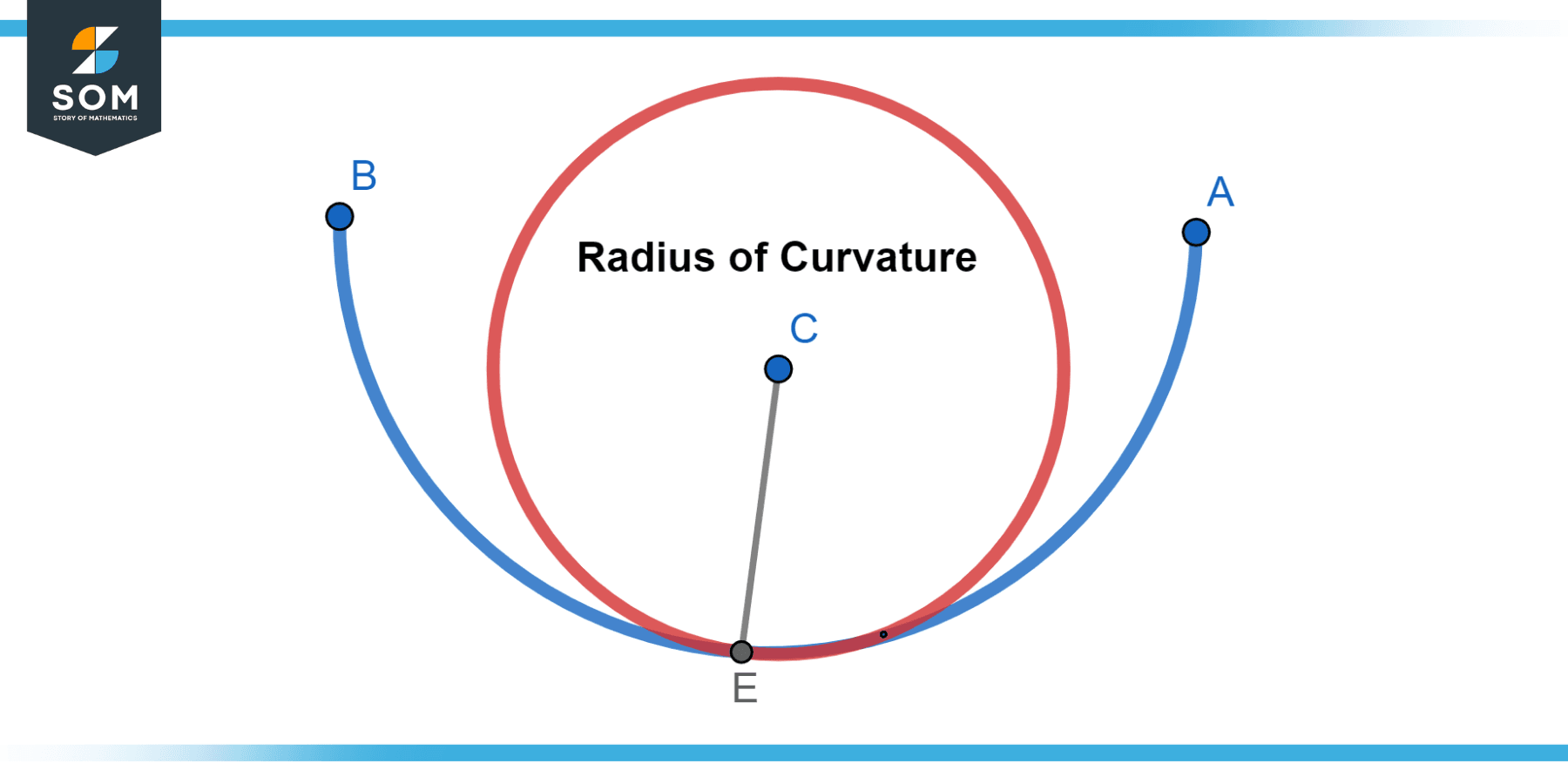
Figure-1.
Properties
Magnitude of Curvature
The magnitude of curvature ∣k∣ measures the sharpness of the curve’s bend. Larger ∣k∣ values mean sharper bends, while smaller values indicate gentler curves.
Direction of Curvature
The sign of curvature indicates the bend’s direction. Positive k (k > 0) signifies a leftward bend when observed from the tangent direction, while negative k (k < 0) signifies a rightward bend.
Circle and Curvature
Circles have constant positive curvature. Curvature , where is the circle’s radius. Larger circles have smaller curvature.
Straight Lines
Straight lines have zero curvature () as they don’t bend.
Inflection Points
Inflection points have changing curvature signs, indicating a change in bending direction.
Local Analysis
The curvature formula examines a curve’s behavior at a single point, not global properties.
Higher Dimensions
The concept extends to higher dimensions, like surfaces in 3D space, using normal vectors.
Applications
Curvature is crucial in geometry, physics, and graphics. It helps design curves, analyze roads, and more.
Parametrization Independence
The curvature formula remains constant for different curve parametrizations. Curvature is intrinsic.
Exercise
Example 1
The Curvature of a Circle
Consider a circle with radius . Find the curvature at any point on the circle.
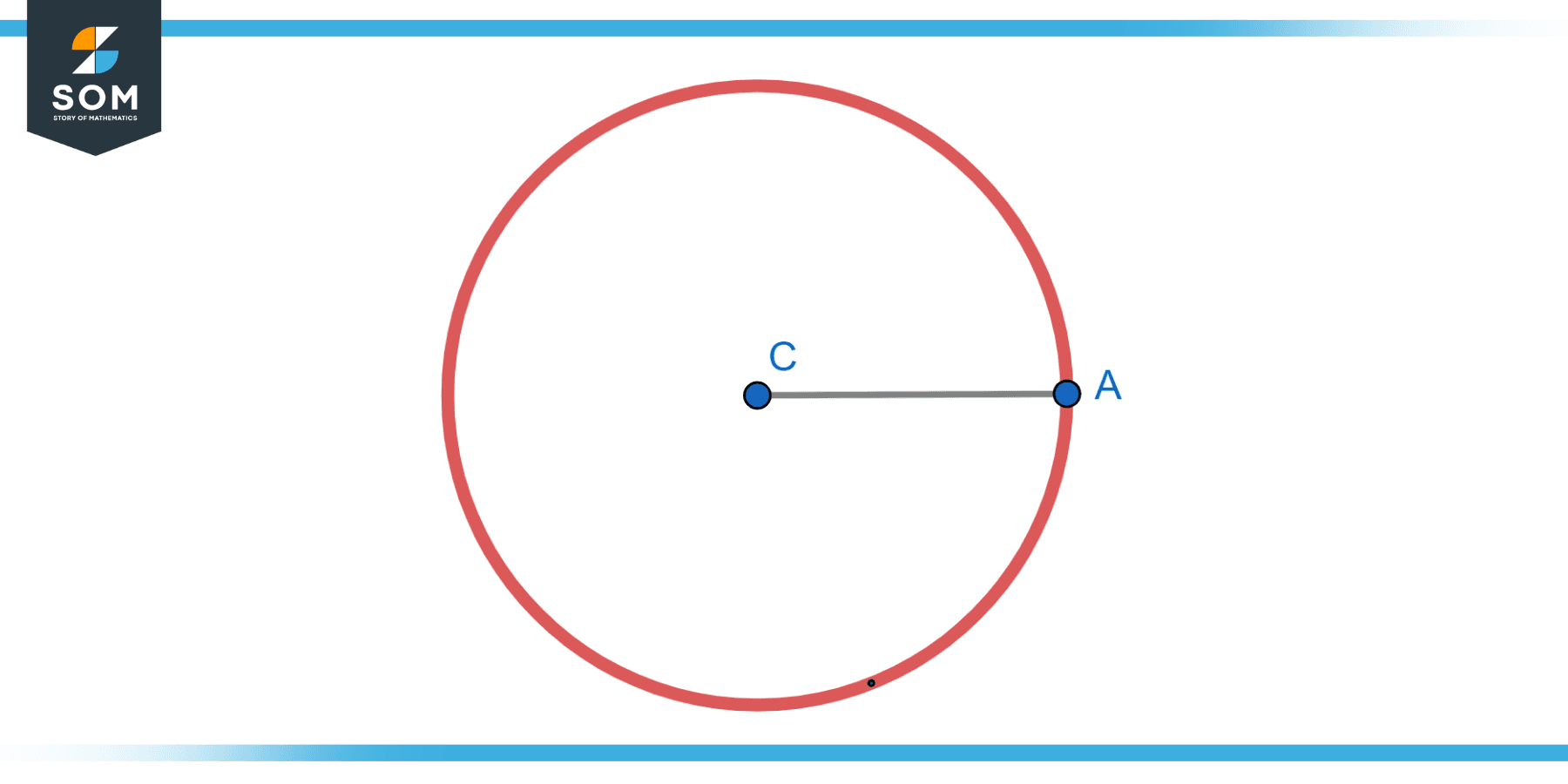
Figure-2.
Solution
For a circle, the curvature is given by . Since the radius is constant for a circle, the curvature is also constant.
Example 2
The Curvature of a Parabola
Find the curvature of the parabola at the origin.
Solution
The parametric equations for the parabola are and . Differentiating, we get:
and
Also,
and
Substitute these values into the curvature formula:
At the origin (), the curvature is .
Example 3
The Curvature of a Straight Line
Find the curvature of the straight line at any point.
Solution
A straight line is a curve with zero curvature everywhere ().
Example 4
The Curvature of an Ellipse
Consider the ellipse $(x^2/a^2 ) + (y^2/b^2)$ . Find the curvature at any point.
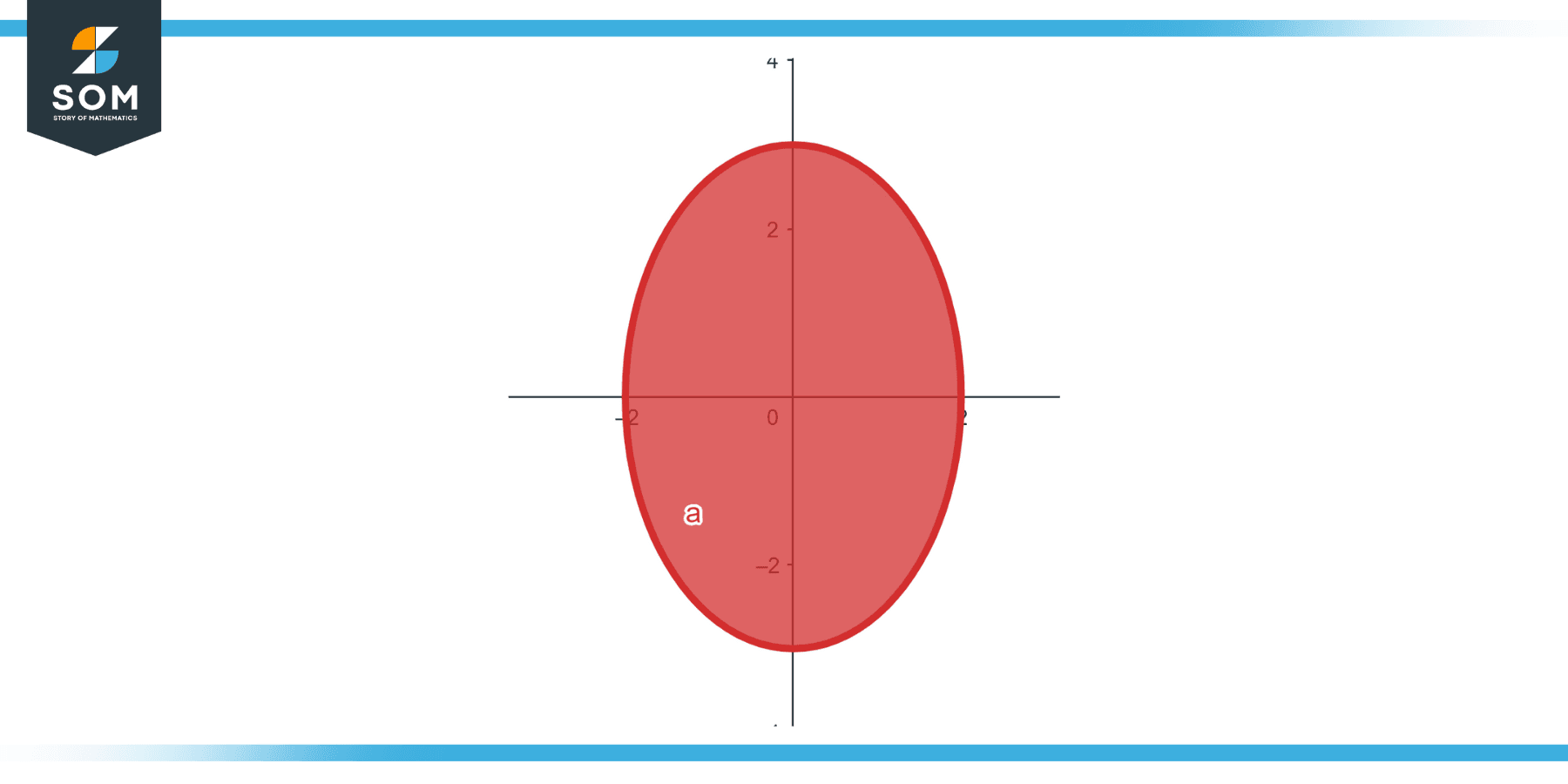
Figure-3.
Solution
Parametric equations for the ellipse are and .
Differentiating and calculating the curvature using the formula will yield a complex expression that simplifies to:
ab/($(a^2 sin^2(t) -b^2cos^2(t) )^{3/2}$).
Example 5
The Curvature of a Hyperbola
Find the curvature of the hyperbola $(x^2/a^2) – (y^2/b^2)$ at any point.
Solution
Parametric equations for the hyperbola are and . Differentiating and calculating the curvature using the formula will yield a complex expression that simplifies to:
ab/($(a^2 sin^2(t) -b^2cos^2(t) )^{3/2}$).
Applications
Geometry and Differential Geometry
Curvature is a fundamental concept in geometry. The curvature formula helps analyze and characterize curves and surfaces. It’s used in understanding the behavior of curves in different geometrical contexts, such as circles, ellipses, and more complex curves.
Physics
In physics, curvature plays a role in understanding the curvature of spacetime in general relativity. It’s also used in the study of particle trajectories, fluid dynamics, and the bending of light in gravitational fields.
Computer Graphics and Animation
Curvature is vital in computer graphics for creating smooth curves and surfaces. It’s used in modeling 3D shapes, designing animations, and ensuring visual realism.
Engineering and Mechanics
Curvature finds applications in structural engineering, where it’s used to analyze the bending behavior of beams and other structural elements. It’s also relevant in the study of mechanical components’ shapes and behavior under forces.
Robotics
Curvature helps in designing and controlling robot motion. It’s used to plan trajectories that navigate robots through various environments without collisions.
Medical Imaging
In medical imaging, curvature analysis is used to study anatomical structures. It aids in understanding the curvature of bones, blood vessels, and other organs, which is important for diagnosis and treatment planning.
Curvature plays a role in navigation algorithms, especially when mapping out routes and calculating optimal paths in various terrains.
Manufacturing and Design
In manufacturing, curvature analysis helps design and produce components with specific shapes, ensuring their functional and aesthetic requirements are met.
Mathematics Education
The curvature formula is often used as an example to teach calculus and differential geometry concepts to students. It helps illustrate the practical applications of mathematical concepts.
Art and Architecture
Architects and artists use curvature concepts to create aesthetically pleasing designs with smooth lines and pleasing curves. Curvature is also considered in designing structural elements to ensure stability.
Astronomy
In astronomy, curvature comes into play when considering the bending of light due to gravity. This phenomenon is used to study gravitational lensing and to observe objects that are behind massive astronomical bodies.
Urban Planning
Curvature can be used to design roads and transportation systems with smooth turns and minimal discomfort for users.
Historical Background
The historical evolution of the curvature formula spans centuries of mathematical progress. Initially, ancient Greek mathematicians like Euclid and Apollonius laid the foundations of geometry, but curvature wasn’t a central focus.
It was in the 17th century that René Descartes introduced Cartesian coordinates, which allowed algebraic representation of curves. However, the concept of curvature didn’t gain prominence at this point.
The 18th century saw the emergence of calculus by Gottfried Wilhelm Leibniz and Isaac Newton, providing tools for curve analysis, though their focus was on tangents and rates of change.
It wasn’t until the 19th century that Carl Friedrich Gauss made a significant breakthrough, introducing the concept of intrinsic curvature. He formulated the Gaussian curvature for surfaces, which paved the way for modern differential geometry.
Bernhard Riemann further expanded on Gauss’s work, introducing the notion of Riemannian geometry. His innovations formed the basis for understanding curvature in non-Euclidean spaces.
In the 20th century, mathematicians like Élie Cartan continued refining the theory of curvature. Differential geometry found applications in physics, most notably in Albert Einstein’s theory of general relativity, where curvature describes the bending of spacetime due to mass.
This gradual evolution transformed the curvature formula from a geometric curiosity to a fundamental concept that underpins our understanding of the shape and structure of curves, surfaces, and spaces in mathematics and physics.
All images were created with GeoGebra.