JUMP TO TOPIC

Decagons, with their intriguing shape and symmetrical properties, have captivated mathematicians, artists, and architects for centuries. The Greek terms “deka,” which means “ten,” and “gonia,” which means “angle,” a Decagon is a polygon with ten sides and ten angles.
Brief Overview of the Article
We will investigate the interesting universe of Decagons in this thorough article, elucidating their properties, construction methods, and practical applications. From their geometric intricacies to their presence in art, architecture, and nature, Decagons offer a wealth of knowledge and beauty. Join us on this geometric journey as we delve into the depths of Decagons and uncover their secrets.
Definition of a Decagon
A decagon is a polygon with ten sides and ten interior angles. It is derived from the Latin words “deka,” meaning ten, and “gonia,” meaning angle. A defining characteristic of a decagon is that all of its sides have equal lengths, and all of its interior angles have equal measures. The sum of the interior angles in a decagon is 1440 degrees, with each angle measuring 144 degrees.
A decagon exhibits several geometric properties that make it an intriguing shape to study. One of its notable features is rotational symmetry. It can be rotated by multiples of 36 degrees around its center and still look the same, as each side and angle maintains its relative position. This property makes the decagon aesthetically pleasing and balanced.
Decagons also possess lines of symmetry. There are ten lines of symmetry in a decagon, each passing through its center and bisecting opposite sides. These lines divide the decagon into congruent halves, reflecting the shape’s symmetry.
Decagons find applications in various fields, such as architecture, engineering, and design. In architecture, decagonal shapes are seen in the design of buildings, pavilions, and monuments. Engineers may use decagons to create stable structures, such as bridges or trusses, due to their balanced distribution of forces.
The study of decagons and their properties extends beyond mathematics and into other areas, such as art, where they can serve as inspiration for aesthetically pleasing designs and patterns. Understanding the characteristics and properties of decagons allows for their effective use in different contexts, demonstrating the significance and versatility of this ten-sided polygon. Below is the geometric diagram of a decagon.
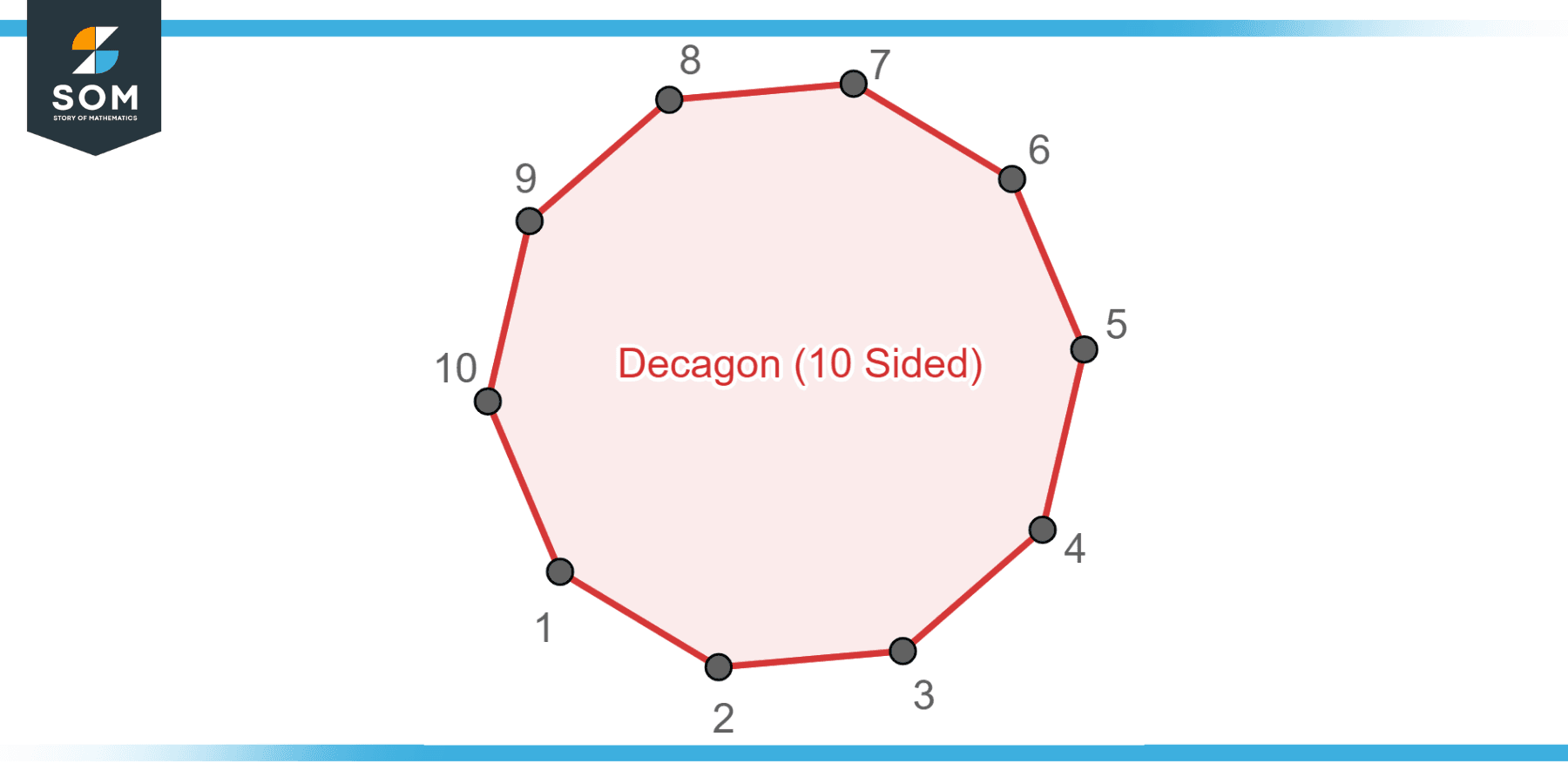
Figure-1: Decagon
Brief history and significance of Decagons in mathematics and geometry
Mathematical and geometric research on decagons has a long history that reaches back to antiquity. The significance of decagons in these domains can be summarised as follows:
Ancient Origins
The fascination with geometric shapes, including decagons, can be linked to historic civilizations like the Egyptians, Babylonians, and Greeks. The Greeks, in particular, made significant contributions to the understanding of decagons and other polygons. Mathematicians like Pythagoras, Euclid, and Archimedes explored the properties of decagons and other regular polygons, establishing the foundations of geometry.
Geometric Constructions
The ancient Greeks developed methods for constructing decagons using only a compass and straightedge. One such method involves the construction of a regular pentagon, followed by the division of each of its sides into two equal segments. Connecting these points creates a regular decagon. These geometric constructions were essential in understanding and exploring the properties of decagons.
Regular Polygons
Decagons belong to the family of regular polygons, which are polygons with equal side lengths and equal interior angles. Regular polygons have been a subject of fascination and study in mathematics due to their inherent symmetry and mathematical properties. Decagons, with their ten sides and angles, hold a special place among regular polygons.
Trigonometry and Angle Measures
Decagons played a role in the development of trigonometry, the area of mathematics concerned with the connections between triangles’ angles and sides. It is possible to define trigonometric functions like sine, cosine, and tangent using decagons and other regular polygons. The study of decagons contributed to the understanding of angle measures and trigonometric identities.
Tessellations and Patterns
Decagons have been employed in the creation of intricate tessellations, which are repeating patterns that cover a plane without any gaps or overlaps. Artists and mathematicians have explored the use of decagons in tessellations to create visually captivating and mathematically intriguing designs.
Geometry of Decagon
Side Length
In a regular decagon, all ten sides have the same length. To calculate the length of each side, you can use the formula s = c / (2 × sin(π/10)), where s represents the side length and c is the length of the circumradius (the distance from the center of the decagon to any of its vertices).
Angle Measures
In a regular decagon, all ten interior angles have the same measure. The measure of each interior angle can be calculated using the formula A = (n-2) × 180° / n, where A represents the measure of each angle, where n is the polygon’s number of sides. For a decagon, each interior angle measures 144 degrees.
The angles created by extending one side of the decagon and the subsequent interior angle are known as the exterior angles of a decagon. In a regular decagon, each exterior angle measures 36 degrees. The total of all outside polygonal angles, including a decagon, is always 360 degrees.
Diagonals
A diagonal of a decagon is a line segment that connects two non-adjacent vertices. In a decagon, there are 35 diagonals. The following formula can be used to determine the number of diagonals in any polygon:
D = (n × (n – 3)) / 2
where n represents the number of sides of the polygon.
Symmetry
A regular decagon possesses both rotational symmetry and reflectional symmetry. It can be rotated by multiples of 36 degrees (360 degrees divided by 10) around its center and still maintain its original appearance. Additionally, there are ten lines of symmetry that pass through the center and bisect opposite sides of the decagon, dividing it into congruent halves.
Area
The area of a decagon can be calculated by dividing it into ten isosceles triangles. To find the area of each triangle, you can use the formula A = (1/2) × base × height. Drawing a perpendicular line from the decagon’s center to one of its sides will reveal the height and base of the shape, respectively. Multiply the area of one triangle by 10 to get the total area of the decagon.
Decagon Types
Decagons can be classified into different types based on their properties and characteristics. Here are three types of decagons:
Regular Decagon
A regular decagon is a type of decagon where all ten sides and angles are equal. The length of each side is the same, while the size of each inner angle is 144 degrees. A regular decagon exhibits high symmetry, including rotational symmetry and multiple lines of symmetry. It is considered the most symmetrical and balanced type of decagon. Below is the diagram for a regular decagon.
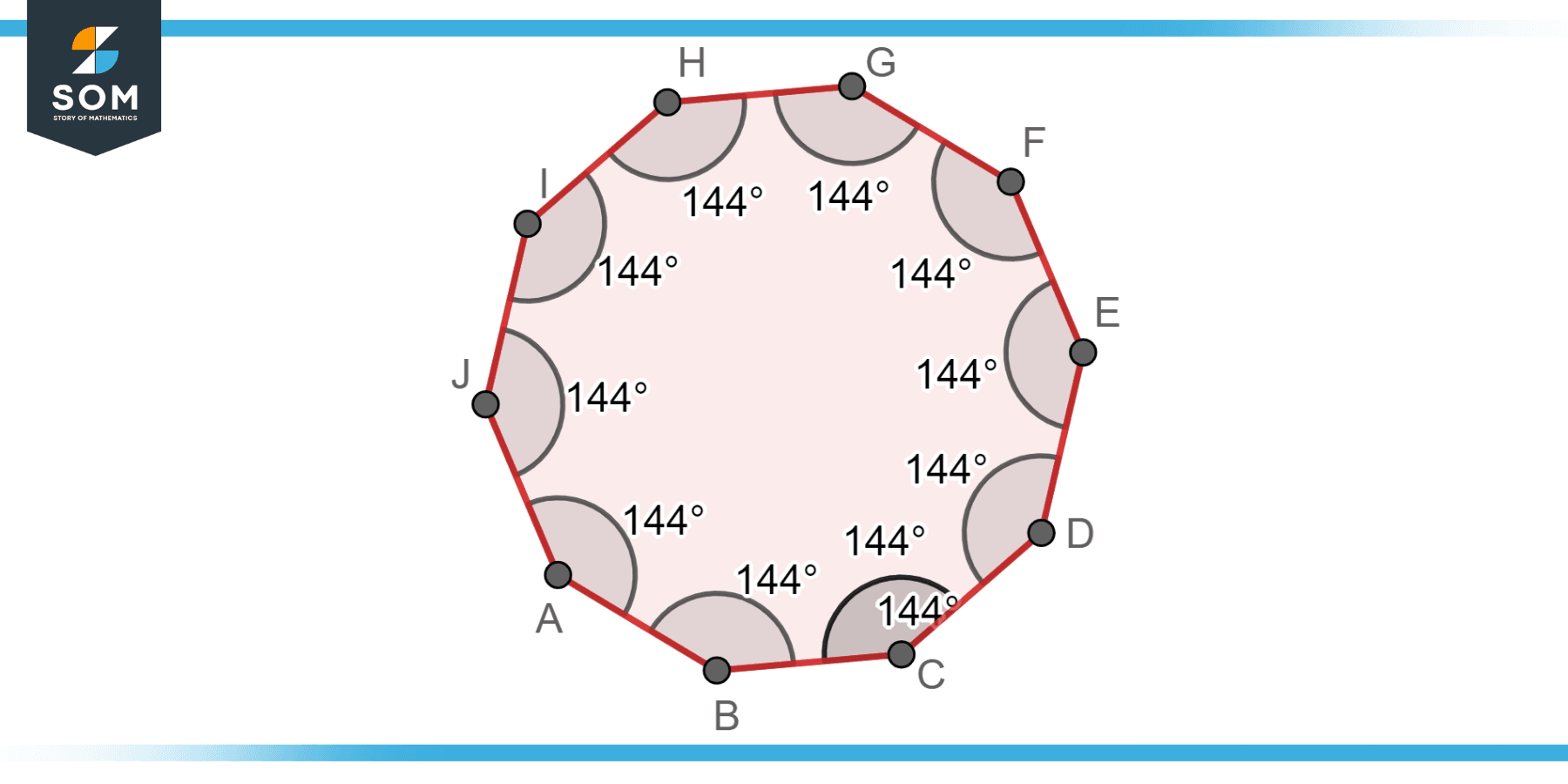
Figure-2: Regular decagon.
Irregular Decagon
An irregular decagon is a decagon that does not have equal side lengths or equal interior angles. In an irregular decagon, the lengths of the sides and the measures of the angles can vary. Irregular decagons can have a diverse range of shapes and configurations, making them less symmetric compared to regular decagons. Below is the geometric diagram of an irregular decagon.
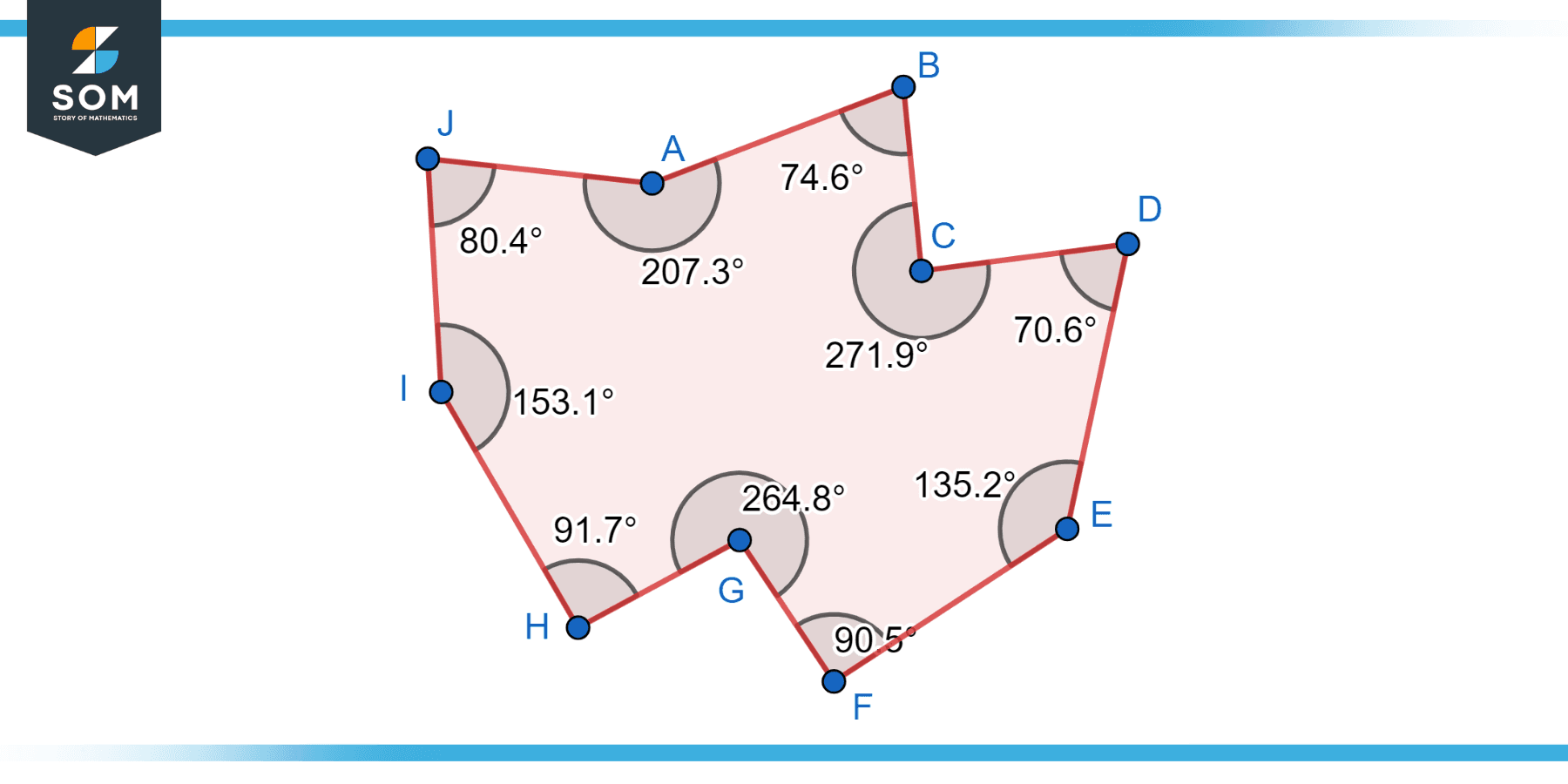
Figure-3: Irregular decagon.
Convex Decagon
A convex decagon is a decagon where all interior angles are less than 180 degrees. In other words, none of the sides “bend inwards.” In a convex decagon, any line segment connecting two points inside the decagon lies entirely within the shape. Regular decagons are always convex, However, irregular decagons with at least one internal angle greater than 180 degrees can be either convex or concave. Below is the geometric diagram of an irregular decagon.
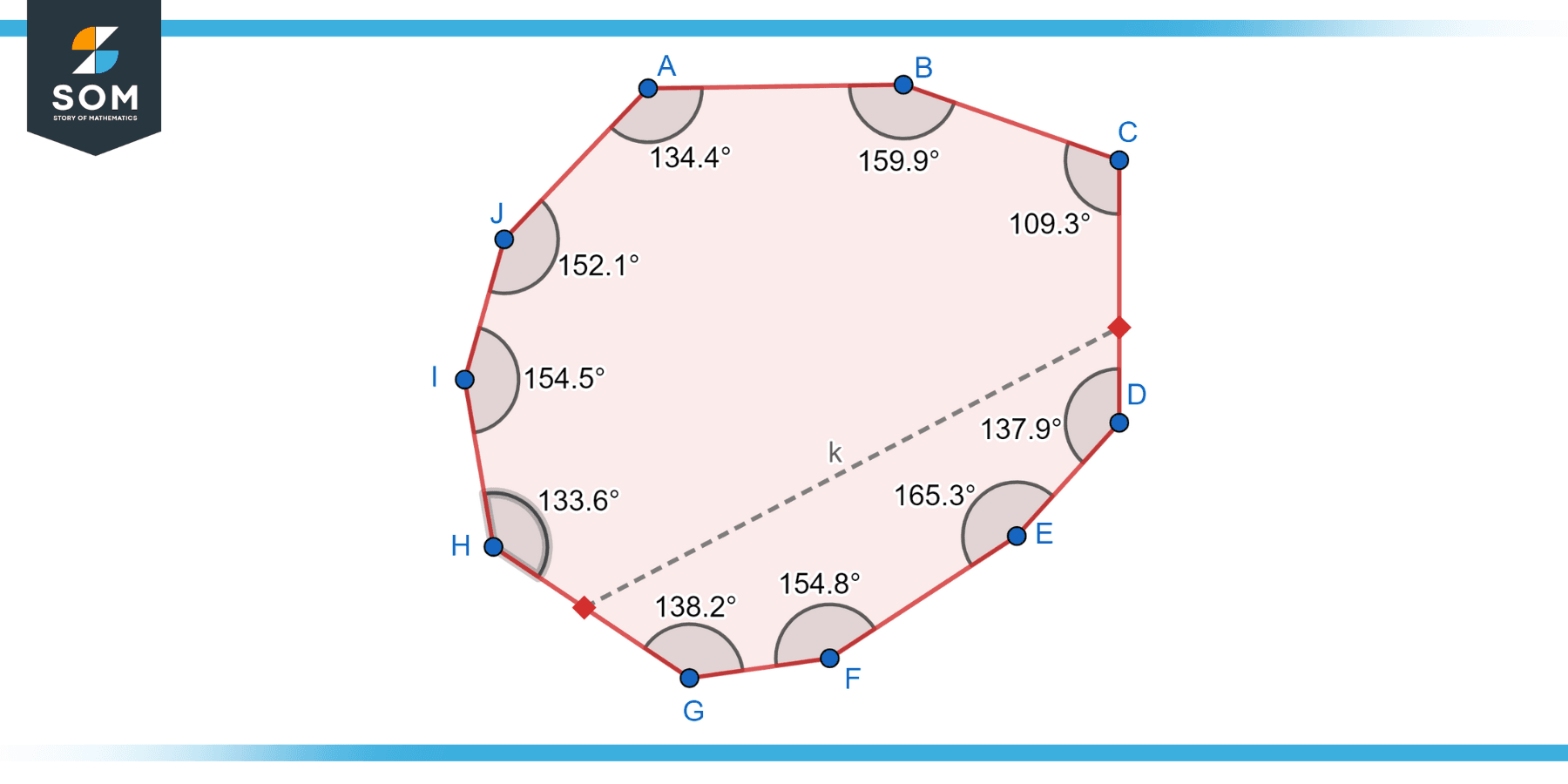
Figure-4: Convex decagon.
Related Formulas
In this section, we present some related formulas commonly used in calculations involving decagons, such as determining perimeter, angle measures, area, or the number of diagonals. They provide a mathematical framework to analyze and understand different aspects of decagons.
Perimeter (P)
The perimeter of a decagon is the sum of all its side lengths. For a regular decagon, where all sides have equal length, the perimeter can be calculated using the formula P = 10×s, where s represents the length of each side.
Interior Angle Measure (A)
In a regular decagon, all ten interior angles have the same measure. The measure of each interior angle can be calculated using the formula A = (n-2) × 180° / n, where A represents the measure of each angle and n is the number of sides of the polygon. For a decagon, each interior angle measures 144 degrees.
Exterior Angle Measure (E)
The exterior angles of a decagon are the angles formed by extending one side of the decagon and an adjacent interior angle. In a regular decagon, each exterior angle measures 36 degrees.
Area (A)
The area of a decagon can be calculated by dividing it into ten isosceles triangles. To find the area of each triangle, you can use the formula A = (1/2) × base ×height. The base is the length of one side of the decagon, and the height can be found by drawing a perpendicular line from the center of the decagon to one of its sides. Multiply the area of one triangle by 10 to get the total area of the decagon.
Diagonals (D)
A diagonal is a line segment that joins two polygonal vertices that are not contiguous to one another. The number of diagonals in a decagon can be calculated using the formula D = (n × (n – 3)) / 2, where n represents the number of sides of the polygon. In the case of a decagon, there are 35 diagonals.
Real-World Applications of Decagons
Decagons, with their unique geometric properties, have various real-world applications across different fields. The distinctive geometric properties and visual appeal of decagons make them valuable design elements in various fields, adding interest and enhancing aesthetics in architectural, artistic, and industrial contexts. Below we present a few practical applications in the real world.
Stop Signs
One of the most well-known examples of decagons in everyday life is the stop sign. Stop signs are octagonal in shape, with a decagonal red border. The unique shape of the decagon helps it stand out from other road signs, serving as a clear visual indicator for drivers to come to a complete stop at intersections.
Construction
The symmetrical and balanced nature of decagons makes them appealing for the design of buildings, facades, windows, and decorative elements. Decagonal floor plans or rooms are sometimes incorporated into architectural designs for their aesthetic appeal.
Art and Design
Decagons serve as a source of inspiration for artists and designers. The symmetrical and regular shape of a decagon can be used as a framework for creating patterns, sculptures, and other art forms. Artists and designers often incorporate decagonal elements into their works to achieve visual balance and harmony.
Jewelry Design
Decagonal shapes can be found in jewelry design, especially in the creation of pendants, brooches, or earrings. The angularity and balanced proportions of a decagon lend themselves well to jewelry aesthetics, allowing for unique and eye-catching designs.
Sporting Equipment
Decagonal shapes can be found in various sporting equipment. For instance, soccer balls and some basketballs have decagonal patterns on their surfaces. These patterns not only add visual appeal but also help with grip and ball control during gameplay.
Landscaping and Garden Design
Decagons can be incorporated into landscape architecture and garden design. They can be used as foundations for circular raised beds or planting areas. Decagonal structures, such as gazebos or pergolas, can be introduced to add architectural interest and create focal points in gardens or parks.
Tiling and Flooring
Decagonal tiles or flooring patterns are utilized in interior design and flooring applications. These geometric patterns can add visual interest and break the monotony of traditional square or rectangular tile arrangements. Decagonal tiles can be arranged in different ways, including tessellations or radial patterns, to create unique and captivating floor designs.
Industrial Design
The shape of decagons can inspire the design of products and industrial objects. The symmetrical and regular form of a decagon can be incorporated into product design, such as electronics, furniture, or automotive components, to create aesthetically pleasing and balanced designs.
Architecture
Decagons can be seen in architectural designs, particularly in the construction of buildings, pavilions, and monuments. Some structures feature decagonal floor plans, while others incorporate decagonal shapes in decorative elements such as windows, archways, or domes. The inclusion of decagons in architecture adds aesthetic interest and a sense of uniqueness to the design.
Exercise
Example 1
Given a regular decagon with a side length of 5 units, calculate its perimeter.
Solution
The perimeter of a decagon is the sum of all its side lengths. Since a regular decagon has equal side lengths, we can multiply the side length by the number of sides (which is 10) to find the perimeter.
Perimeter = 10 × side length
Perimeter = 10 × 5 = 50 units
Therefore, the perimeter of the regular decagon is 50 units.
Example 2
Calculate the size of each internal decagonal angle.
Solution
For a regular decagon, the formula to determine the size of each interior (decagonal) angle is A = (n-2) × 180° / n, where A represents the measure of each angle and n is the number of sides of the polygon (which is 10 for a decagon).
Plugging in the values:
A = (10 – 2) × 180° / 10
A = 8 × 180° / 10
A = 144°
Therefore, each interior angle of a regular decagon measures 144 degrees.
Example 3
Calculate the number of diagonals in a decagon.
Solution
The formula to calculate the number of diagonals in any polygon is D = (n × (n – 3)) / 2, where D represents the number of diagonals and n is the number of sides of the polygon (which is 10 for a decagon).
Plugging in the values:
D = (10 × (10 – 3)) / 2
D = (10 × 7) / 2
D = 70 / 2
D = 35
Therefore, a decagon has 35 diagonals.
Example 4
Given a regular decagon with a side length of 6 units, find its area.
Solution
We can partition a regular decagon into 10 congruent isosceles triangles to determine its area. The area of one triangle can be calculated using the formula A = (1/2) × base × height.
Since the base of each triangle is the side length of the decagon (6 units), we need to find the height. To find the height, we can draw a line segment from the center of the decagon to one of its sides, creating a right triangle. The height is the distance along a perpendicular axis from the centre to a side.
The height of a regular decagon can be calculated using the formula h = c × cos(π/10), where c represents the length of the circumradius (the distance from the center of the decagon to any vertex).
Plugging in the values:
h = 6 × cos(π/10)
h ≈ 5.3028 units
Now, we can calculate the area of one triangle:
A = (1/2) × base × height
A = (1/2) × 6 × 5.3028
A ≈ 15.9084 square units
Since there are ten congruent triangles, the total area of the decagon is:
Total Area = 10 × A
Total Area ≈ 159.084 square units
Therefore, the area of the regular decagon is approximately 159.084 square units.
Example 5
Calculate the size of each of a decagon’s exterior angles.
Solution
The exterior angles of a decagon are the angles formed by extending one side of the decagon and an adjacent interior angle. In a regular decagon, each exterior angle measures 360° / 10 = 36 degrees. Consequently, a decagon’s outer angles are each measured is 36 degrees.
Example 6
Which of the following structures given in Fig-5 is not a decagon?
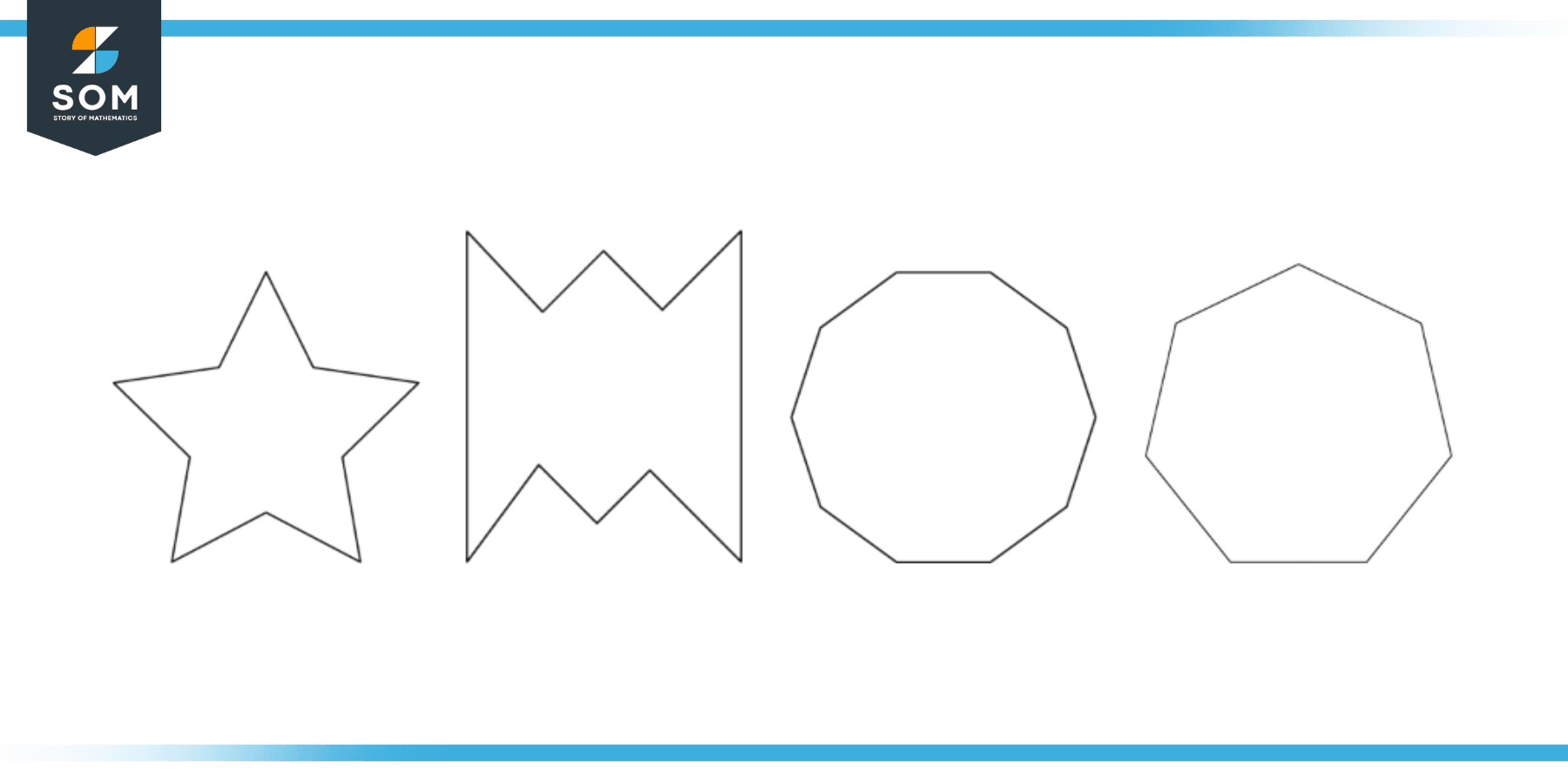
Figure-5
Solution
As we can see, there are both regular and irregular polygons. Three polygons have 10 sides and there is one shape that has 7 sides. A heptagon is a seven-sided polygon and not a decagon. Hence, the shape in the image is not a decagon is given as;

All images were created with GeoGebra.
