JUMP TO TOPIC

Step into the enchanting world of polygons, where shapes take on mesmerizing forms and captivate our mathematical curiosity. Among these intriguing geometric wonders, the dodecagon stands as a testament to the intricacy and elegance found within the realm of twelve-sided polygons. The dodecagon has fascinated mathematicians, architects, and artists for centuries with its symmetrical structure and harmonious angles.
This article takes us on a fascinating journey through the dodecagon, peeling back the layers of its geometry, uncovering its remarkable properties, and discovering its real-world applications. Join us on this illuminating journey as we unravel the mysteries of the dodecagon and gain a deeper appreciation for its timeless allure.
Definition
A dodecagon is a polygon with twelve sides and twelve interior angles. The term “dodecagon” is derived from the Greek words “dodeka,” meaning twelve, and “gonia,” meaning angle. A defining characteristic of a dodecagon is that its sides have equal lengths, and its interior angles have equal measures. In a regular dodecagon, all twelve sides and angles are congruent.
The dodecagon exhibits several geometric properties that make it a fascinating shape to study. Its symmetrical structure creates a sense of balance and harmony. Regular dodecagons have internal angles that are each 150 degrees in length, and the total interior angle length for all dodecagons is 1800 degrees.
The dodecagon can be visualized as a closed figure formed by connecting twelve straight line segments, with each segment representing a side. The sides of the dodecagon do not intersect each other, and they enclose a unique region of space.
Understanding the definition of a dodecagon allows us to explore its properties, relationships with other polygons, construction techniques, and applications in various fields. It’s distinctive characteristics and geometric attributes make the dodecagon an intriguing subject of study in mathematics, art, architecture, and other disciplines. Below is the generic diagram of the dodecagon.
Figure-1: Generic dodecagon.
Historical Significance
The historical significance of the dodecagon lies in its role as a fundamental polygon in mathematical and architectural contexts throughout history. We gain insights into its profound influence on mathematics, architecture, symbolism, and cultural expressions throughout different periods of history. It is evidence of the geometric shapes’ enduring appeal and admiration, as well as their significant influence on human civilisation. Below are a few aspects that highlight its historical significance.
Ancient Mathematics
The study of polygons, including the dodecagon, held great importance in ancient mathematics. The ancient Greeks, particularly mathematicians like Pythagoras, Euclid, and Archimedes, explored the properties and relationships of polygons, laying the foundation for the development of geometry. The dodecagon, as a regular polygon, played a prominent role in their geometric investigations.
Architectural Symbolism
The dodecagon held symbolic significance in ancient architecture. In civilizations like ancient Egypt and Mesopotamia, regular polygons, including the dodecagon, were incorporated into the design of temples, palaces, and other structures. These geometric shapes were believed to possess mystical and cosmic symbolism, representing concepts such as completeness, harmony, and divine order.
Sacred Geometry
The dodecagon’s geometric properties, along with other regular polygons, were associated with sacred geometry in various cultures. The precision and symmetry of the dodecagon were seen as reflections of cosmic harmony and spiritual principles. This concept influenced the design of religious buildings, artwork, and rituals, illustrating the historical significance of the dodecagon in spiritual and metaphysical beliefs.
Mathematical Foundations
The dodecagon, as a regular polygon, served as a fundamental shape for understanding geometric concepts and formulating mathematical principles. Its properties contributed to the development of formulas, theorems, and calculations related to polygons and angles. The study of the dodecagon, along with other regular polygons, laid the groundwork for advancements in geometry and trigonometry.
Cultural Influence
The dodecagon’s historical significance extends to its cultural impact. Throughout history, artists, architects, and craftsmen drew inspiration from the dodecagon’s aesthetic appeal and geometric properties. It influenced artistic and architectural styles, appearing in decorative motifs, mosaics, and architectural designs. The dodecagon’s presence in cultural artifacts and designs reflects its enduring historical significance.
Properties of Dodecagons
The properties of a dodecagon, a polygon with twelve sides, encompass various geometric aspects, which allow us to analyze its angles, symmetries, and relationships between sides and diagonals. These properties have practical applications in architecture, design, and mathematics, contributing to the understanding and applying geometric concepts. Let’s explore its properties in detail.
Side Length
In a regular dodecagon, all twelve (12) sides have the same length. This means that each side is congruent to one another. In an irregular dodecagon, the side lengths may vary.
The measure of Each Interior Angle in a Regular Dodecagon
The measure of each interior angle in a regular dodecagon can be determined using the formula A = (n-2) * 180° / n, where A represents the measure of each angle and n is the number of sides (which is 12 for a dodecagon).
Measure of Each Interior Angle = (12-2) ×180° / 12 = 150°
The measure of Each Exterior Angle in a Regular Dodecagon
The relationship between exterior angles and internal angles of a polygon can be used to determine the measure of each exterior angle in a regular dodecagon.
In any polygon, the sum of an exterior angle and its corresponding interior angle is always 180 degrees. Since a regular dodecagon has 12 sides, each interior angle measures 150 degrees (as calculated previously).
Therefore, the measure of each exterior angle in a regular dodecagon can be found by subtracting the measure of the corresponding interior angle from 180 degrees.
The measure of Each Exterior Angle = 180° – Measure of Each Interior Angle
Measure of Each Exterior Angle = 180° – 150°
The measure of Each Exterior Angle = 30°
Symmetry
A regular dodecagon possesses rotational symmetry. It can be rotated by multiples of 30 degrees (360 degrees divided by 12) around its center and still maintain its original appearance. It also has twelve lines of symmetry that pass through its center and bisect opposite sides, dividing the dodecagon into congruent halves.
Diagonals
A diagonal is a line segment that joins two polygonal vertices that are not contiguous to one another. A dodecagon has a total of 66 diagonals. The formula to calculate the number of diagonals in any polygon is (n × (n – 3)) / 2, where n represents the number of sides of the polygon.
Apothem
The apothem of a dodecagon is the distance from the center of the dodecagon to any of its sides. In a regular dodecagon, the apothem is equal to the radius of the circumcircle, which is the circle that encircles the dodecagon’s vertices.
Circumradius
The circumradius of a dodecagon is the distance from its center to any of its vertices. In a regular dodecagon, the circumradius is equal to the distance from the center to any of its sides or diagonals.
Perimeter
You may determine a regular dodecagon’s perimeter by multiplying the side length (s) by the number of sides (n), which is 12 for a dodecagon.
Perimeter (P) = 12 × s
Area
The area of a dodecagon can be calculated by dividing it into triangles or using the formula A = (1/2) × apothem × perimeter. For a regular dodecagon, where the apothem and side lengths are known, the area can be calculated more precisely.
Dodecagon Types
Dodecagons, or polygons with twelve sides, can be categorized into a variety of forms according to their traits and qualities. Here are four types of dodecagons:
Regular Dodecagon
A regular dodecagon is a type of dodecagon where all twelve sides and twelve angles are equal. Each side has the same length, and each interior angle measures 150 degrees. A regular dodecagon exhibits high symmetry, including rotational symmetry and twelve lines of symmetry. It is considered the most symmetrical and balanced type of dodecagon. Below is the diagram of a regular dodecagon.
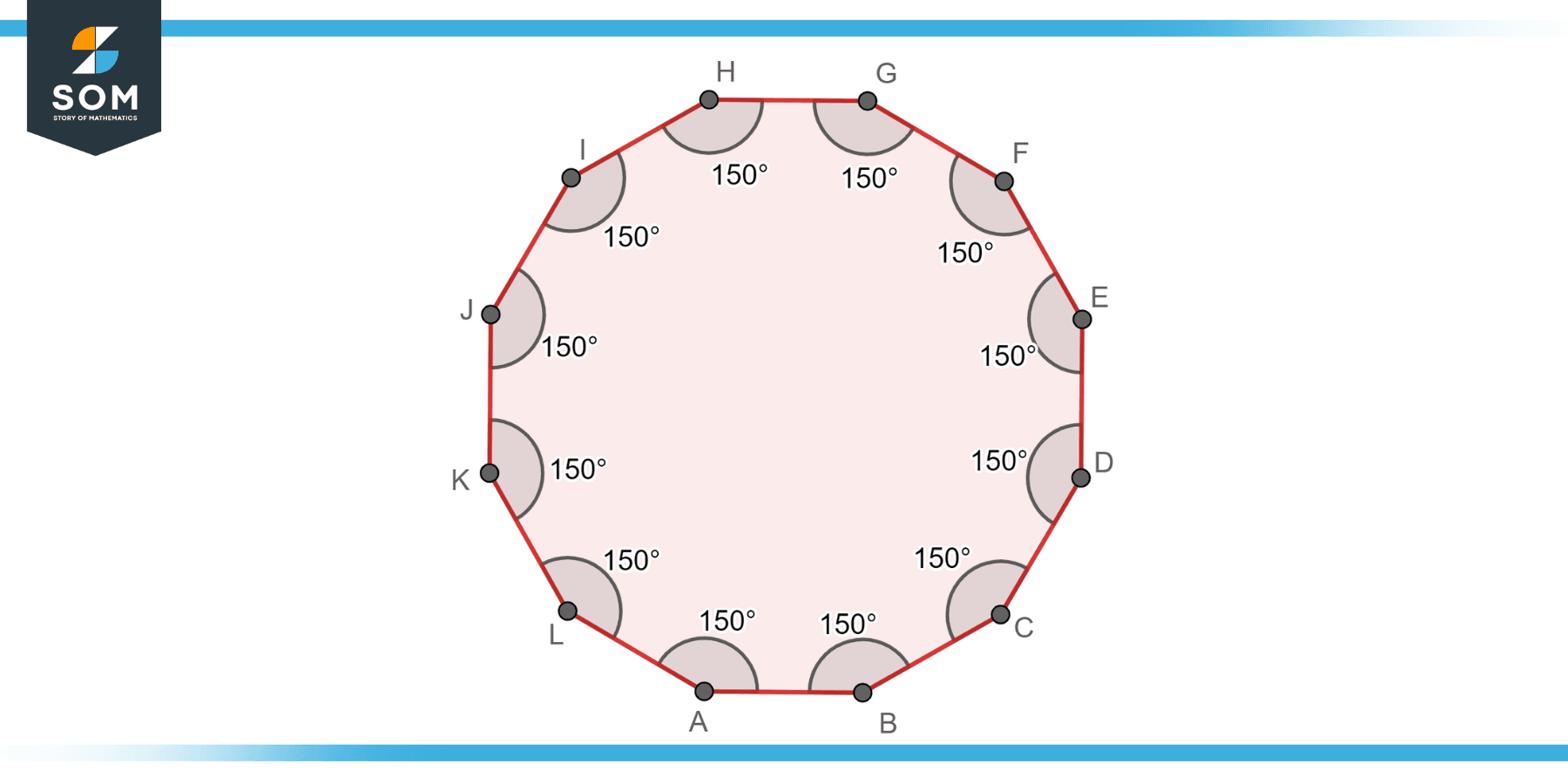
Figure-2: Regular dodecagon.
Irregular Dodecagon
An irregular dodecagon is a dodecagon that does not have equal side lengths or equal interior angles. In an irregular dodecagon, the lengths of the sides and the measures of the angles can vary. Irregular dodecagons can have diverse shapes and configurations, making them less symmetric than regular dodecagons. Below is the generic diagram of the irregular dodecagon.
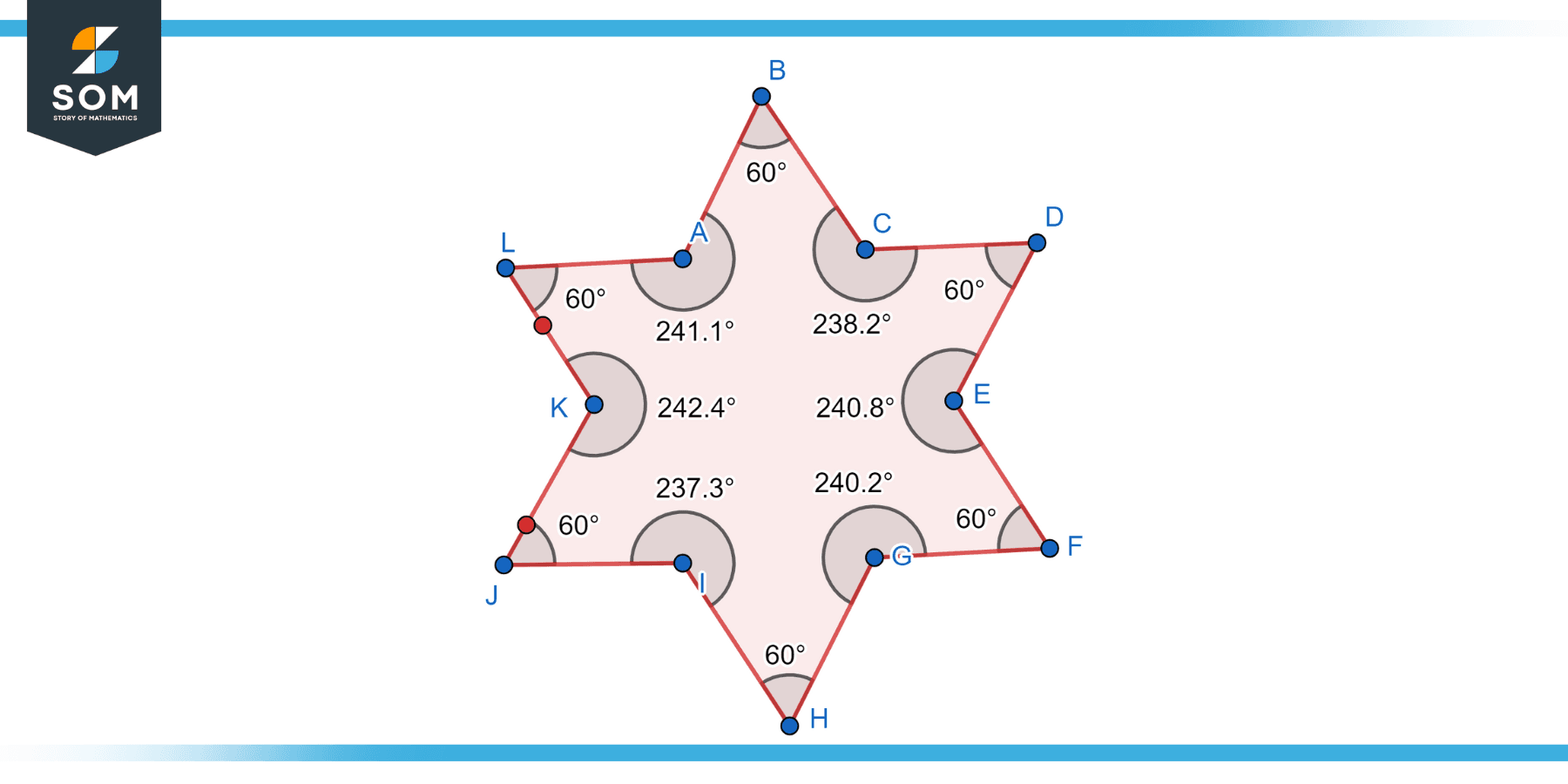
Figure-3: Irregular dodecagon.
Convex Dodecagon
Any dodecagon with inner angles less than 180 degrees is said to be convex. In other words, none of the sides “bend inward” towards the interior of the shape. A convex dodecagon has a “bulging” or “outward” shape, with its sides extending away from the interior. All regular dodecagons are convex, as well as many irregular dodecagons. Below is the diagram of the convex dodecagon.
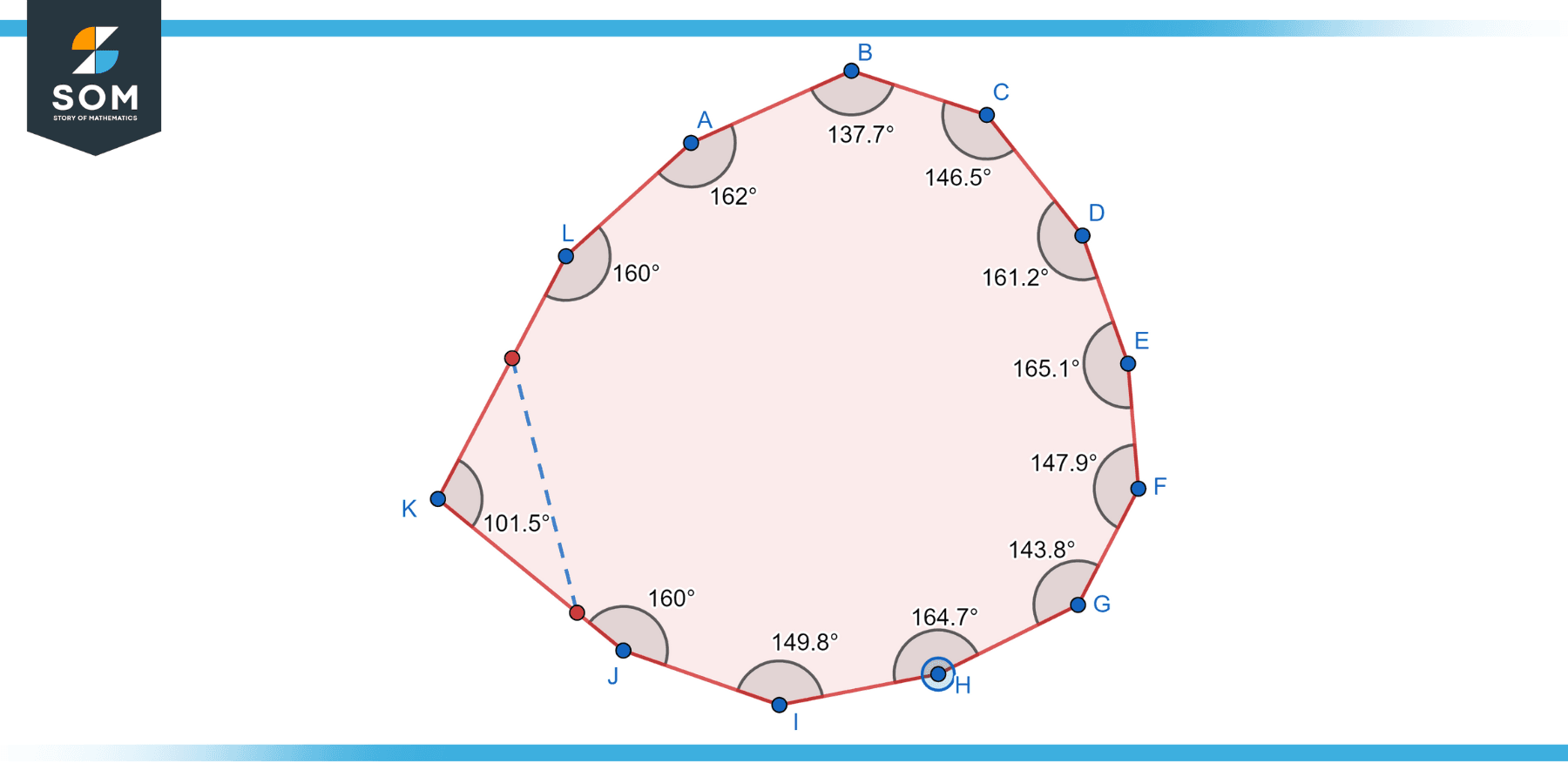
Figure-4: Convex dodecagon.
Concave Dodecagon:
A concave dodecagon is a dodecagon that has at least one interior angle greater than 180 degrees. In a concave dodecagon, one or more sides “bend inward,” causing the polygon to have an indentation or “caved-in” appearance. The bending of sides creates regions within the polygon where the interior angles face inward. Concave dodecagons can have a variety of shapes and configurations, with sections that appear to “cave in” or overlap. Below is the diagram of the concave dodecagon.
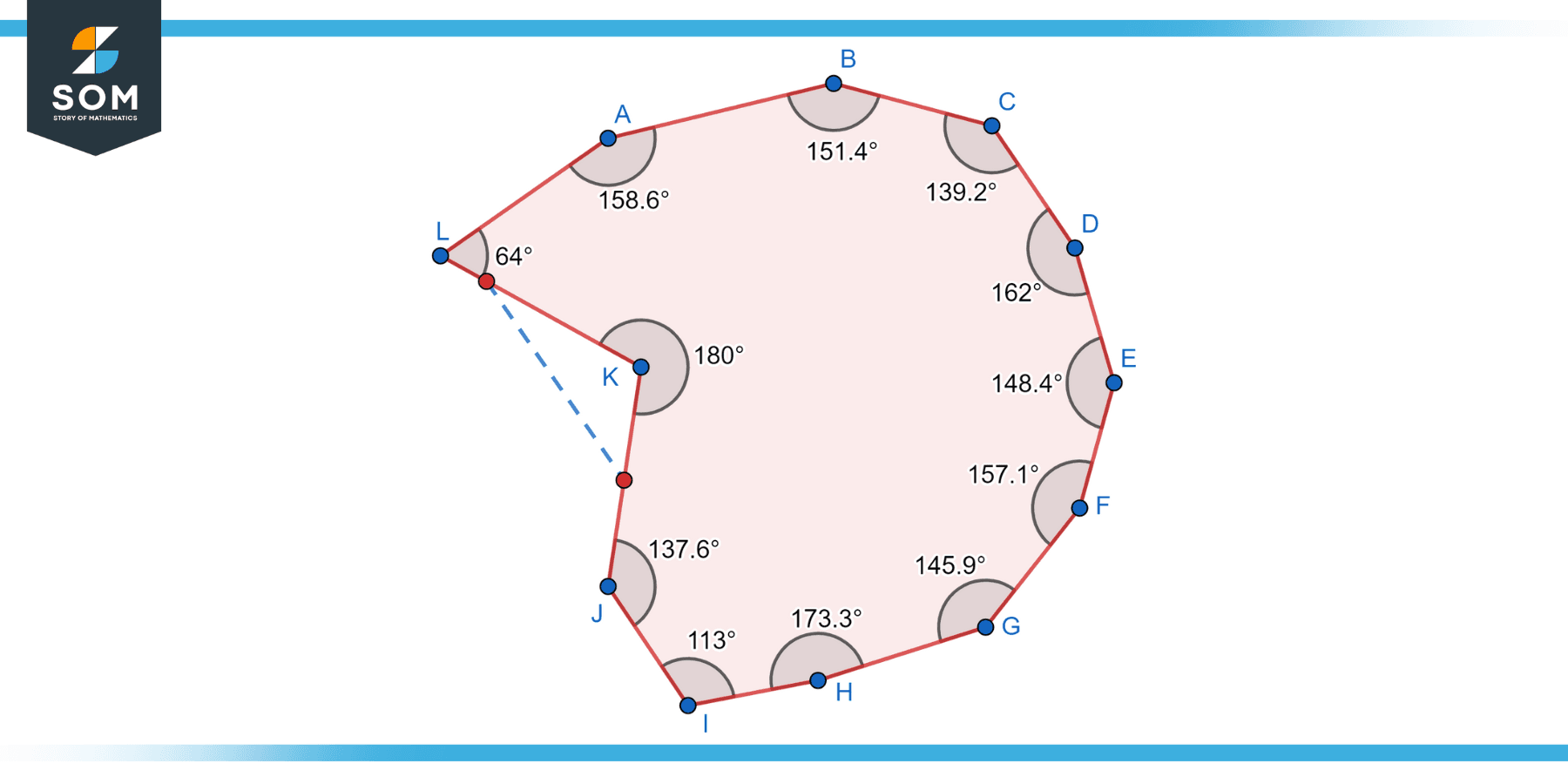
Figure-5: Concave dodecagon.
Applications
While the direct applications of the dodecagon may not be as widespread as some other polygons, its unique properties, symmetrical structure, and visual appeal make it a valuable design element in architecture, art, interior design, landscaping, and educational contexts. By incorporating the dodecagon, the following applications can benefit from its aesthetic and geometric qualities, enhancing the overall experience and visual impact.
Architecture and Design
The symmetrical and visually striking nature of the dodecagon makes it suitable for architectural designs. Dodecagonal floor plans can be used to create unique and aesthetically pleasing spaces in buildings. The shape can also be incorporated into structural elements, such as windows, facades, or decorative motifs, adding a sense of elegance and artistic flair to architectural designs.
Art and Crafts
The dodecagon can serve as a source of inspiration for artists and craftsmen. Its balanced and symmetrical structure can be utilized as a framework for creating patterns, mosaics, or artistic compositions. By incorporating the dodecagon into their work, artists can achieve visually intriguing and harmonious designs in various media, including paintings, sculptures, ceramics, and textiles.
Decorative Elements
The dodecagon’s aesthetic appeal lends itself well to decorative elements in interior design and furniture. It can be incorporated into the design of mirrors, frames, tiles, rugs, or textiles, adding a unique touch to living spaces, hotels, or public areas. The dodecagon’s symmetrical form can create a visually pleasing and balanced atmosphere in interior settings.
Landscaping and Garden Design
The dodecagon can be applied in landscaping and garden design to create visually interesting and harmonious outdoor spaces. For example, dodecagonal pathways or patio designs can add geometric patterns and focal points to gardens. The shape can also inspire the layout of flower beds, hedge arrangements, or the design of pavilions or gazebos.
Educational Tools and Games
The dodecagon can be utilized as an educational tool for teaching geometry and spatial reasoning. It can be incorporated into puzzles, games, or building blocks, providing a hands-on approach to understanding geometric concepts. The dodecagon’s distinct shape and symmetry can engage learners and promote geometric thinking.
Sports Fields
One real-world application of a dodecagon can be found in the design of sports fields or courts. Specifically, the layout of a soccer field can be based on the shape of a dodecagon. While the official rules of soccer require a rectangular field, the inner part of the field where the game is played can be shaped like a dodecagon to accommodate additional space for spectators, team benches, and other facilities.
The dodecagon provides an interesting alternative to the traditional rectangular shape, offering a unique aesthetic appeal and potentially enhancing the viewing experience for spectators. The curved edges of the dodecagon can create more organic and visually pleasing lines compared to the straight lines of a rectangular field. This can contribute to a more immersive and engaging atmosphere during matches.
Exercise
Example 1
Given a regular dodecagon with a side length of 8 units, we want to calculate its perimeter.
Solution
The perimeter of a regular dodecagon can be found by multiplying the side length by the number of sides, which is 12.
Perimeter (P) = 12 × side length
Perimeter (P) = 12 × 8 = 96 units
Therefore, the perimeter of the regular dodecagon is 96 units.
Example 2
Calculate the measure of each interior angle in a regular dodecagon.
Solution
The formula to find the measure of each interior angle of a regular dodecagon is A = (n-2) × 180° / n, where A represents the measure of each angle and n is the number of sides of the polygon (which is 12 for a dodecagon).
Plugging in the values:
A = (12 – 2) × 180° / 12
A = 10 × 180° / 12
A = 150°
Therefore, each interior angle of a regular dodecagon measures 150 degrees.
Example 3
Find out the number of diagonals in a dodecagon.
Solution
The formula to calculate the number of diagonals in any polygon is D = (n * (n – 3)) / 2, where D represents the number of diagonals and n is the polygon’s side count, which for a dodecagon is 12 sides.
Plugging in the values:
D = (12 × (12 – 3)) / 2
D = (12 × 9) / 2
D = 108 / 2
D = 54
Therefore, a dodecagon has 54 diagonals.
Example 4
Calculate the Area of a Regular Dodecagon: Given a regular dodecagon with a side length of 10 units, calculate its area.
Solution
To find the area of a regular dodecagon, we can divide it into triangles. The area of one triangle can be calculated using the formula A = (1/2) × base × height.
Since the base of each triangle is the side length of the dodecagon (10 units), we need to find the height. The height is the length from the center of the dodecagon to one of its sides.
The height of a regular dodecagon can be calculated using the formula $h = a \times \sqrt{(3+2\sqrt{3})}$, where a represents the apothem (the distance from the center to a side).
Plugging in the values:
$$h = 10 \times \sqrt{(3+2\sqrt{3})}$$
h ≈ 29.520 units
Now, we can calculate the area of one triangle:
A = (1/2) × base × height
A = (1/2) × 10 × 29.520
A ≈ 147.6 square units
Since there are twelve congruent triangles, the total area of the dodecagon is:
Total Area = 12 × A
Total Area ≈ 12 × 147.6
Total Area ≈ 1771.2 square units
Therefore, the area of the regular dodecagon is approximately 1771.2 square units.
Example 5
Determine the measure of an exterior angle in a regular dodecagon.
Solution
The sum of the measures of an exterior angle and its corresponding interior angle in any polygon is always 180 degrees. Since a regular dodecagon has 12 sides, each interior angle measures 150 degrees (as calculated in a previous example). Therefore, the measure of each exterior angle can be found by subtracting the interior angle measure from 180 degrees.
Exterior Angle = 180° – Interior Angle
Exterior Angle = 180° – 150°
Exterior Angle = 30°
Therefore, each exterior angle in a regular dodecagon measures 30 degrees.
Example 6
Calculating the Circumference of a Regular Dodecagon: Given a regular dodecagon with a radius of 5 units, we want to calculate its circumference.
Solution
The circumference of a regular dodecagon can be found by multiplying the side length by the number of sides, which is 12 in this case.
Circumference = 12 × Side Length
To find the side length, we can use the formula for the side length of a regular polygon in terms of the radius: Side Length = 2 × radius× tan(180°/n), where n is the number of sides.
Side Length = 2 × 5 × tan(180°/12)
Side Length ≈ 4.0588 units
Now we can calculate the circumference:
Circumference = 12 × Side Length
Circumference ≈ 12 × 4.0588
Circumference ≈ 48.706 units
Therefore, the circumference of the regular dodecagon is approximately 48.706 units.
Example 7
Calculate the sum of the measures of the interior angles and exterior angles in a dodecagon.
Solution
The sum of the measures of the interior angles in any polygon can be calculated using the formula (n-2) × 180°, where n is the number of sides.
Sum of Interior Angles = (12 – 2) × 180°
Sum of Interior Angles = 10 × 180°
Sum of Interior Angles = 1800°
For a regular polygon, the sum of the measures of the exterior angles is always 360°.
Sum of Exterior Angles = 360°
Therefore, the sum of the measures of the interior angles in a dodecagon is 1800 degrees, and 360 degrees is the result of adding the measurements of the exterior angles.
All images were created with GeoGebra.
