JUMP TO TOPIC
The multiplication property of inequality states that if both sides of an inequality are multiplied or divided by the same positive number, it will result in an equivalent inequality.
For example, if $x<y$ and we multiply the both sides by $m$, then $xm < ym$ and similarly if we divide both sides by “$m$”, then $\dfrac{x}{m} < \dfrac{y}{m}$. The multiplication property will work the same if $x > y$, the outcome in this case will be $xm > ym$ and $\dfrac{x}{m} > \dfrac{y}{m}$, respectively.
Multiplication Property of Inequality Definition
The multiplication property of inequality states that if one side of the inequality is multiplied or divided by a positive number, then we can multiply and divide the other side of the inequality by the same number without changing or disturbing the direction sign of inequality.
This property is used to solve linear equations. Solving inequalities, specifically linear inequalities, can be made easy by using the properties of the multiplication of the inequality. The multiplication property of inequality is the same as the division property of inequality; for example, if we want to divide “$6$” by “$2$”, we can multiply it by $\dfrac{1}{2}$. It can also be used along with the addition property to solve the linear equation.
In practical scenarios, inequalities are used to determine the maximum available profit from the production of an item. These can also determine the best combination of drugs to cure a disease, etc. This topic will help you understand the concept of the multiplication property of inequality, and you can use this method to solve inequalities’ problems afterward.
Consider three variable number $x$,$y$ and $z$, such that $z \neq 0$. Then according to the multiplicative property of the inequality, we can have four cases.
Case: 1
If $z > 0$ and $x > y$, then $xz > yz$
For example, if $x = 2$ and $y =1$ and we multiply the inequality equation $x>y$ by “z” which is equal to $4$, then the value of “x” and “y” will be “4” and “1” respectively.
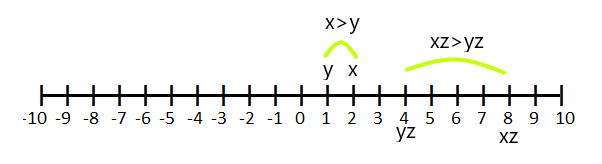
Case: 2
If $z > 0$ and $x < y$, then $xz < yz$
For example, if $y = 2$ and $x =1$ and we multiply it by “$4$” then x.z (4) will still remain smaller than y.z (8).
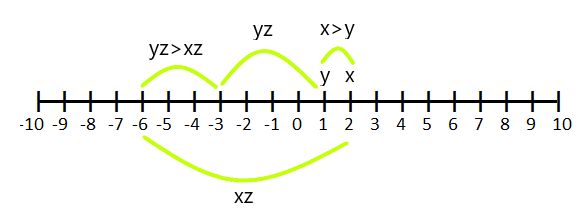
Case: 3
If $z < 0$ and $x > y$, then $xz < yz$
For example, if $x = 2$ and $y =1$ and we multiply it by “$-3$” then (y.z) becomes greater than (x.z)
Case: 4
If $z < 0$ and $x < y$, then $xz > yz$
For example, just swap the values of the example discussed in case 3. If $x = 1$ and $y = 2$ and we multiply it by $z = -3$, then (x.z) becomes greater than (y.z)
We can see from the above cases if we multiply an inequality expression with a positive number, it does not switch the inequality sign, but if we multiply the expression with a negative number on both sides, it will switch the direction of the inequality sign.
How To Solve Inequalities Using Multiplication Property of Inequality
This property can be used to solve the normal and fraction inequalities. If we are given a fraction equation with a common denominator, we can easily remove the denominator by multiplying both sides of the inequality by the denominator. For example, we can simply $\dfrac{x}{2} > \dfrac{3}{2}$ by multiplying both sides by “$2$”.
Similarly, many real-life problems related to inequalities require using multiplication property. Lets us discuss various numerical and word problems related to inequalities.
The inequality problems can be solved by combining all three properties:
- multiplication
- addition property of inequality
- subtraction property of inequality
Let us now study the multiplication property of inequality examples.
Example 1:
Solve for the “$x$” for the given inequality expressions
1) $\dfrac{6}{7}x > \dfrac{3}{7}$
2) $\dfrac{3}{5}x > {9}$
3) $-4x +2 < 2x +4$
4) $3x > 9$
5) $\dfrac{3}{2}x < -\dfrac{3}{2}$
Solution:
The given terms are in fraction form, and solving them using the multiplication property of inequality is also known as the multiplicative inverse property of inequality. Remember, inequalities can also include negative numbers, but the sign of inequality will only change when we divide or multiply the inequality by a negative number.
1)
$\dfrac{6}{7}x > \dfrac{3}{7}$
Multiplying both sides by “$7$”
$6x > 3$
$x > \dfrac{3}{6}$
$x > \dfrac{1}{2}$
Alternatively, we can solve this question more quickly as our primary focus should be the removal of the coefficient with “$x$”. We can multiply both sides with “ $\dfrac{7}{6}$” and then solve the rest of the equation.
$\dfrac{6}{7}x > \dfrac{3}{7}$
$\dfrac{6}{7} \times \dfrac{7}{6}x > \dfrac{3}{7} \times \dfrac{7}{6}$
$x > \dfrac{3}{6}$
$x > \dfrac{1}{2}$
2)
$\dfrac{3}{5}x > 9$
Multiplying both sides by “$5$”
$(\dfrac{3}{5}x) \times 5 > 9 \times 5$
$3x > 45$
$x > \dfrac{45}{3}$
$x > 15$
Alternatively, we can solve this question more quickly by isolating the variable “$x$” from the coefficient and we can do that by multiplying both sides by “$\dfrac{5}{3}$”. If we multiply both sides by “$\dfrac{5}{3}$”, we can write the equation as
$(\dfrac{3}{5}x) \times \dfrac{5}{3} > 9 \times \dfrac{5}{3}$
$x > 3 \times 5$
$x > 15$.
$\dfrac{6}{7} \times \dfrac{7}{6}x > \dfrac{3}{7} \times \dfrac{7}{6}$
$x > \dfrac{3}{6}$
$x > \dfrac{1}{2}$
3)
$-4x + 2 < 2x +4$
First, let us combine the terms with the variable “$x$” on one side and the constant values on the other side.
$-4x -2x < 4 -2$
$-6x < 2$
We have to isolate “$x$” from its coefficient, so we will multiply both sides by “$-\dfrac{1}{6}$”. As you can see, we are multiplying with a negative number; hence we have to switch the inequality sign.
$-6x \times (-\dfrac{1}{6}) > 2 \times (-\dfrac{1}{6})$
$x > -\dfrac{1}{3}$
4)
$3x > 9$
Multiplying both sides by “$\dfrac{1}{3}$”
$(3x) \times \dfrac{1}{3} > 9 \dfrac{1}{3}$
$x > 3$
5)
$-\dfrac{3}{2}x < \dfrac{3}{2}$
We have to isolate “$x$” from its coefficient, so we will multiply both sides by “$-\dfrac{2}{3}$”. As you can see, we are multiplying with a negative number, hence we have to switch the inequality sign.
$(-\dfrac{3}{2}x) \times (-\dfrac{2}{3}) < \dfrac{3}{2} \times (-\dfrac{2}{3})$
$x > – 1$
Example 2:
Write the following equations after multiplying them with “$2$” and “$-2$”.
1) $2x > \dfrac{1}{2}$
2) $\dfrac{1}{4}x > 8$
3) $3x < -4$
4) $2x > 5$
Solution:
1)
$2x > \dfrac{1}{2}$
Let us solve the equation by multiplying both sides by “$2$”
$2x \times 2 > (\dfrac{1}{2}) \times 2$
$4x > 1$
$x > \dfrac{1}{4}$
Now solve the equation by multiplying both sides by “$-2$”
$2x \times (-2) < (\dfrac{1}{2}) \times (-2)$
$-4x < – 1$
$x < \dfrac{1}{4}$
2)
$\dfrac{1}{4}x > 8$
Let us solve the equation by multiplying both sides by “$2$”
$(\dfrac{1}{4}x) \times 2 > 8 \times 2$
$\dfrac{1}{2}x > 16$
$x > 32$
Now solve the equation by multiplying both sides by “$-2$”
$(\dfrac{1}{4}x) \times (-2) < 8 \times (-2)$
$-\dfrac{1}{2}x < -16$
$x < 32$
3)
$3x < -4$
Let us solve the equation by multiplying both sides by “$2$”
$3x \times 2 < -4\times 2$
$6x < -8$
$x < -\dfrac{6}{8}$
$x < -\dfrac{3}{4}$
Now solve the equation by multiplying both sides by “$-2$”
$3x \times 2 < -4\times 2$
$6x < -8$
$x < -\dfrac{6}{8}$
$x < -\dfrac{3}{4}$
4)
$2x > 5$
Let us solve the equation by multiplying both sides by “$2$”
$2x \times 2 > 5 \times 2$
$4x > 10$
$x > \dfrac{10}{4}$
$x > \dfrac{5}{2}$
Now solve the equation by multiplying both sides by “$-2$”
$2x \times (-2) < 5 \times (-2)$
$-4x < -10$
$x < \dfrac{-10}{-4}$
$x < \dfrac{5}{2}$
Solving Word Problems
We have discussed numerical problems related to inequality, now let us see some word problems and solve them.
Example 3:
Suppose a water tank has a maximum capacity of $50$ gallons. If the water tank is filled with $2$ gallons of water in a minute, then by using the multiplication property of inequality, calculate the time required to fill the tank (the capacity should be under $50$ gallons as we don’t want to overflow the tank).
Solution:
Let us say that “$n$” is the number of times in minutes we can fill the tank to its maximum capacity, so we can write the inequality equation as:
$2n \leq 50$
Now, if we multiply both sides of the equation of $\dfrac{1}{2}$, it will give us the time that is required to fill the tank to its maximum capacity.
$(\dfrac{2}{2}) n \leq \dfrac{50}{2}$
$n \leq 25$
Hence, the tank can be filled in less than or equal to $25$ minutes.
Example 4:
Allice has various gift cards for an online retail store, and she can buy stuff for less than $\$ 100$. Allice wants to purchase glass plates with the gift cards, and one plate costs $\$5.5$. Determine the number of plates Allice can buy using the multiplication property of inequality.
Solution:
Let us say “$n$” is the total number of plates, then we can write the inequality equation as:
$5.5 n < 100$
Now if we multiply both sides of the equation of $\dfrac{1}{5.5}$, it will give us the expected number of plates we can buy:
$(\dfrac{5.5}{5.5}) n < \dfrac{100}{5.5}$
$n < 18.18$
Hence, Allice can buy $18$ plates in total from the available gift cards.
Practice Questions:
1. A Farmer is putting up a rectangular fence across the wheat field to keep off stray animals. The total outer boundary is less than or equal to $50$ft. Write the inequality equation to express the length and width of the fence. If the width of the fence is 10 ft, what would be the length of the fence?
2. William has a total amount of $\$400$, and he is planning to spend $\$200$ or less to buy shirts from the sale during a sale gala in a close-by mall. If the price of one shirt is $\$40$, determine the number of shirts William can buy during this sale gala.
3. Tania is throwing a birthday party for her friends. She wants to buy boxes of chocolates and candies for her friends. The price of one box of chocolate is $\$10$, and the price of one box of candies is $\$5$. Tania has a total of $\$500$, but she wants to spend $\$300$ or less; if she buys $18$ chocolate boxes, how many boxes of candies she can buy?
Answer Key:
1.
The outer boundary of the fence is basically the perimeter of the rectangular fence, so we can write the equation for the given data as:
$2 (l+w) \leq 50$
$2 (l + 10) \leq 50$
$2l +20 \leq 50$
$2l \leq 30$
Multiplying both sides by $\dfrac{1}{2}$
$ l \leq 15$
2.
Let “$n$” be the number of shirts, then we can write the equation as:
$40n \leq 200$
$n \leq \dfrac{200}{40}$
$n \leq 5$
3.
Let the “$c$” be the boxes of chocolates and “ b” be the boxes of candies, then we can write the equation as:
$5b + 10c \leq 300$
Tania buys $12$ chocolate boxes, $c =18$
$5b + 10 (18) \leq 300$
$5b + 180 l\leq 300$
$5b \leq 120$
Multiplying both sides by $\dfrac{1}{5}$
$b \leq 25$