Derivative of Sec^2x: Detailed Explanation and Examples

The derivative of $sec^{2}x$ is equivalent to the product of $2$, $sec^{2}x$ and $tanx, i.e., (2. sec^{2}x. tanx)$.

The derivative of this trigonometric function can be determined by various methods, but generally, it is calculated using the chain rule, quotient rule and the product rule of differentiation.

In this complete guide, we will discuss how to differentiate the secant square along with some numerical examples.

What Is the Derivative of Sec^2x?

The derivative of $sec^2x$ is equal $2.sec^{2}(x).tan(x)$, and mathematically, it is written as $\dfrac{d}{dx} sec^2x = 2.sec^{2}x.tanx$. Differentiation of a function gives the slope function of the curve of the function. The graph for the derivative of $sec^{2}x$ is shown below.

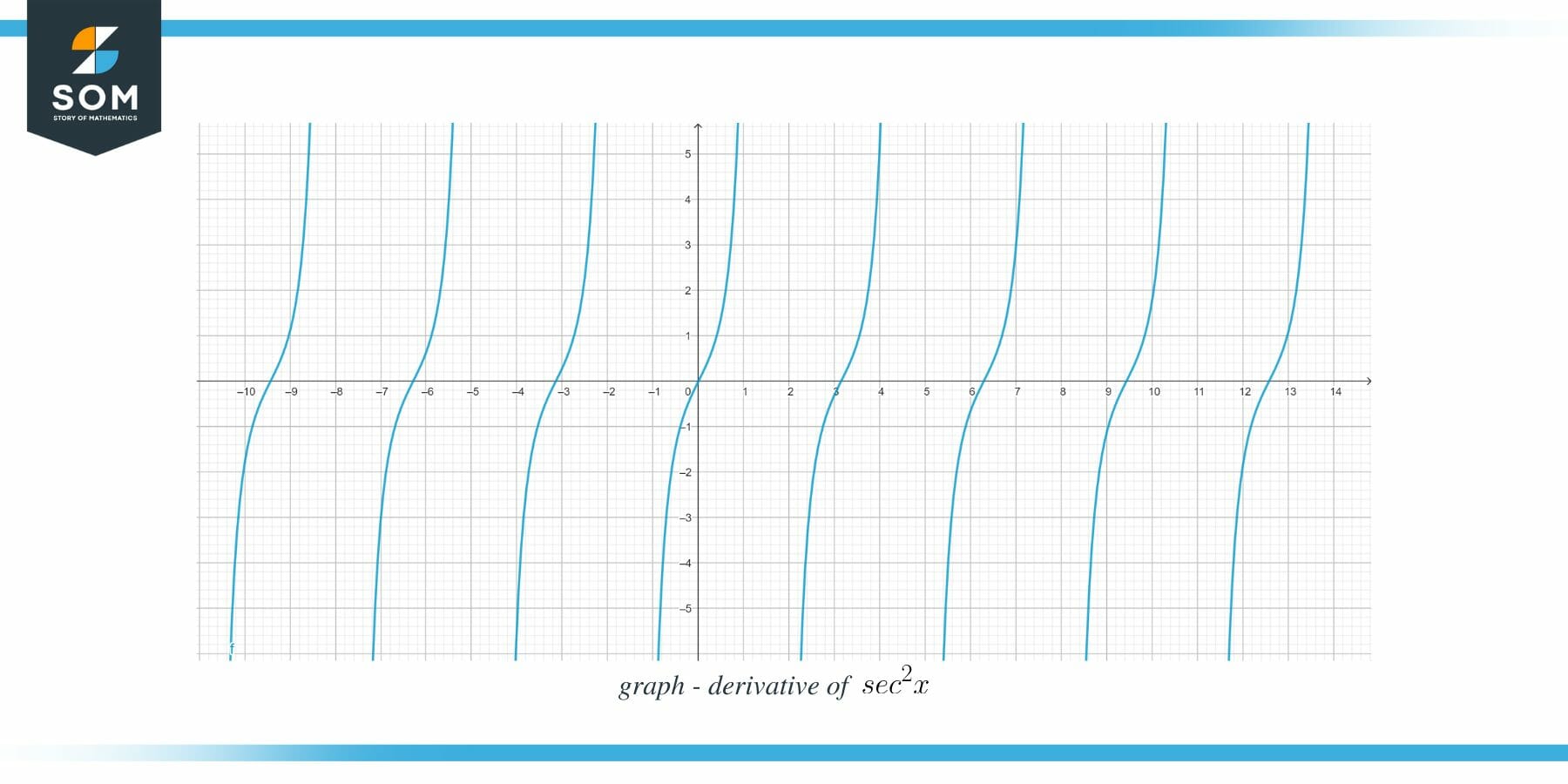
To calculate the derivative of the $sec^{2}x$, it is essential that you know all the basics and all the rules related to differentiation, and you can study or revise them at large. Let us now discuss different methods which can be used to calculate the derivative of the $sec^{2}x$.

Different Methods To Calculate Derivative of Sec^{2}x

There are a few methods which can be used to determine the derivative of $sec^{2}x$, and some of them are listed below.

1. Derivative of Sec Square x by first principle method
2. Derivative of Sec Square x by derivative formula
3. Derivative of Sec Square x by using the Chain Rule
4. Derivative of Sec Square x by using the product rule
5. Derivative of Sec Square x using the quotient rule

Derivative of Secant Square x Using First Principle Method

The derivative of secant square x can be calculated through first principle or by the ab-initio method. The derivative of $sec^2x$ by the first principle method is the method which is taught early during the introduction of derivatives of trigonometric functions, and it utilizes the concept of limit and continuity. This method is like the basic or first method, which is taught to derive the derivatives of any function.

This method is complex as it requires the utilization of different limit rules and trigonometric formulas.

Let $y = sec^{2}x$

$y + \delta y = sec^{2}(x + \delta x)$

$\delta y = sec^{2}(x + \delta x) – y$

$\delta y = sec^{2}(x + \delta x) – sec^{2}x$

We know that $a^{2} – b^{2} = (a+b) (a-b)$

$\delta y = (sec(x+ \delta x) + sec x) (sec(x+ \delta x) – sec x)$

$\delta y = [(sec(x+ \delta x) + sec x)] (\dfrac{1}{cos (x+ \delta x)} – \dfrac{1}{cos x})$

$\delta y = [(sec(x+ \delta x) + sec x)] (\dfrac{cosx – cos (x+ \delta x)}{cos (x+ \delta x). cos x }$

$\delta y = [\dfrac {(sec(x+ \delta x) + sec x)}{cos (x+ \delta x). cos x}] cosx – cos (x+ \delta x)$

$\delta y = [\dfrac {(sec(x+ \delta x) + sec x)}{cos (x+ \delta x). cos x}] cos x – [cos x cos \delta x – sinx sin\delta x)]$

Dividing both sides “ $\delta x$” and putting the limit as $\delta x$ approaches zero.

$\lim_{\delta x \to 0 } \dfrac{\delta y }{\delta x} = \lim_{\delta x \to 0} [\dfrac {(sec(x+ \delta x) + sec x)}{cos (x+ \delta x). cos x}] cos x [ \dfrac{1 – cos \delta x} {\delta x} + sinx \dfrac {sin\delta x}{\delta x} ]$

We know that $\lim_{\delta x \to 0 } \dfrac{1 – cos \delta x} {\delta x} = 0$, $\lim_{\delta x \to 0 } \dfrac{sin \delta x} {\delta x} = 1$

And that $\lim_{\delta x \to 0 } \dfrac{\delta y }{\delta x} = \dfrac{dy}{dx}$

$\dfrac{dy}{dx} = \lim_{\delta x \to 0} [\dfrac {(sec(x+ \delta x) + sec x)}{cos (x+ \delta x). cos x}] + sinx sin\delta x ]$

$\dfrac{dy}{dx} = [\dfrac {(sec x + sec x)}{cos x. cos x}] sinx$

$\dfrac{dy}{dx} = [\dfrac {(2sec x )}{cos^{2} x}] sinx$

$\dfrac{dy}{dx} = [\dfrac {(2sec x )}{cos x}] \dfrac{sinx}{cos x}$

$\dfrac{dy}{dx} = [ (2sec x) (sec x)] tan x$

$\dfrac{dy}{dx} = 2.sec^{2}x.tanx$

Derivative of Secant Square x Using Derivative Formula

The derivative of the secant square can easily be calculated by using the derivative formula. The general derivative formula for any exponential expression can be given as

$\dfrac{d}{dx} x^{n} = n . x^{n – 1}. \dfrac{d}{dx}x = n.x^{n-1}$

For the expression secant square x the value of n will be 2. Hence, if use this formula on secant square x:

$\dfrac{d}{dx} sec^{2}x = 2 . sec^{2 – 1}. \dfrac{d}{dx} sec(x) = 2. sec(x) . sec(x) .tan(x) = 2.sec^{2}x. tanx$

This method is simple and easy, but people often get confused by the general formula as most of the time the formula for exponential expression is given as $\dfrac{d}{dx} x^{n} = n . x^{n – 1}$. The last part is excluded as the derivative of “$x$” is 1. Hopefully, after reading this section, you now know exactly how to calculate the secant square x by using the derivative formula.

Derivative of Secant Square x Using Chain Rule

The derivative of secant square x can be calculated by using the chain rule of differentiation. The chain rule of differentiation is used when we are dealing with or solving composite functions.

A composite function is a function in which one function can be represented in terms of the other function. For example, if we have two functions f(x) and h(x) then a composite function will be written as ( f o h) (x) = f (h(x)). We are writing function “f” in terms of function “h”, and if we take the derivative of this function, then it will be represented as $(f o h)'(x) = f’ (h(x)). h'(x)$.

The trigonometric function $sec^{2}x$ is a composite function as it is the composition of two functions a) $f(x) = x^{2}$ b) $h(x) = sec(x)$. As a composite function, it will be written as $(f o h) (x) = sec^{2}x$. If we apply the chain rule:

$(f o h)’ (x) = f’ (h(x)). h'(x)$.

$(f o h)'(x) = \dfrac{d}{dx} sec^{2}x. \dfrac{d}{dx} sec(x)$

We know that derivative of sec(x) is $sec(x).tan(x)$.

$(f o h)’ (x) = 2. sec (x) . sec (x) .tan (x)$

$(f o h)’ (x) = 2. sec^{2} (x) . tan (x)$

Derivative of Secant Square x Using Product Rule

The derivative of secant square x can be calculated by using the product rule. The product rule is one of the most common methods to solve different algebraic and trigonometric equations. If we write $sec^{2}x$ as the product $sec(x) \times sec(x)$, then we can solve it by using the product rule.

According to product rule, if two functions f(x) and h(x) are multiplied together g(x) = f(x). h(x) and we want to take the derivative of their product, then we can write the formula as $g'(x) = f(x)’h(x) + f(x) h'(x)$.

$sec^{2}x = sec(x) . sec(x)$

$\dfrac{d}{dx} sec^{2}x = sec'(x) sec(x) + sec(x) . sec'(x)$

$\dfrac{d}{dx} sec^{2}x = sec(x). tan(x). sec(x) + sec(x) . sec(x) .tanx(x)$

$\dfrac{d}{dx} sec^{2}x = sec^{2}(x). tanx(x) + tan(x) . sec^{2}(x)$

$\dfrac{d}{dx} sec^{2}x = sec^{2}(x). tanx(x) [ 1+ 1]$

$\dfrac{d}{dx} sec^{2}x = 2. sec^{2}(x). tanx(x)$

Hence, we have proved that the derivative of $sec^{2}x$ is equal to $2. sec^{2}(x). tan(x)$.

Derivative of Secant Square x Using Quotient Rule

The derivative of secant square x can also be calculated by using the quotient rule of differentiation. It is considered the most complex one among all the methods we have discussed so far, but you should know each and every method as this method can help you out in solving other complex questions.

According to the quotient rule, if we are given two functions f(x) and h(x) as a ratio $\dfrac{f(x)}{h(x)}$ then the derivative of such a function is given as $g'(x) = (\dfrac{f}{h})’ = \dfrac{f’h – f h’}{h^{2}}$.

To solve secant square x by using the quotient rule, we will have to take the reciprocal of the trigonometric function. We know that the reciprocal of sec(x) is $\dfrac{1}{cos(x)}$, so the reciprocal of $sec^{2}x$ will be $\dfrac{1}{cos^{2}x}$. Let us now apply the quotient rule and see whether we get the correct answer or not.

$\dfrac{d}{dx} \dfrac{1}{cos^{2}(x)} = \dfrac{(1)’ cos^{2}x – (cos^{2}x)’ 1}{(cos^{2}x)^{2}}$

$\dfrac{d}{dx} \dfrac{1}{cos^{2}(x)} = \dfrac{(0).cos^{2}x – (-2.cosx. sinx)) }{(cos^{4}x)}$

$\dfrac{d}{dx} \dfrac{1}{cos^{2}(x)} = \dfrac{ 2.cosx. sinx }{(cos^{4}x)}$

$\dfrac{d}{dx} \dfrac{1}{cos^{2}(x)} = \dfrac{ 2.sinx }{(cos^{3}x)}$

$\dfrac{d}{dx} \dfrac{1}{cos^{2}(x)} = \dfrac{ 2 }{(cos^{2}x)} . \dfrac{ sinx }{(cos x)}$

$\dfrac{d}{dx} \dfrac{1}{cos^{2}(x)} = 2. sec^{2}x . tan(x)$

Hence, we have proved that the derivative of $sec^{2}x$ is $2. sec^{2}x . tan(x)$ by using the quotient rule.

Example 1: Is the derivative of Hyperbolic secant square x the same as that of trigonometric secant square x?

Solution:

No, the derivative of $sech^{2}x$ is a little different from that of $sec^{2}x$. Actually, the only difference between these two derivative functions is that of a negative sign. The derivative of $sech^{2}x = -2.sech(x).tan(x)$.

Let us solve for the derivative of $sech^{2}x$

We know that the derivative of $sech(x) = -sech(x) .tanh(x)$

Let us apply the chain rule of differentiation on $sech^{2}x$

$\dfrac{d}{dx} sech^{2}x = 2. sech(x). \dfrac{d}{dx} sech(x)$

$\dfrac{d}{dx} sech^{2}x = 2. Sech(x). (-sech(x).tanh(x))$

$\dfrac{d}{dx} sech^{2}x = -2. sech^{2}(x). tanh(x)$

Example 2: Prove that derivative of $(1+ tan^{2}x)$ is equal to the derivative of $sec^{2}x$.

We know that the trigonometric identity involving secx and tanx can be written as $sec^{2}x – tan^{2}x = 1$. So we can write it as:

$sec^{2}x = 1 + tan^{2}x$.

So let us replace $sec^{2}x$ with $1 + tan^{2}x$ and see if the derivative of $1 + tan^{2}x$ is equal to $sec^{2}x$.

$\dfrac{d}{dx} (1 + tan^{2}x) = \dfrac{d}{dx} 1 + \dfrac{d}{dx} tan^{2}x$

$\dfrac{d}{dx} (1 + tan^{2}x) = 0 + 2. tanx. \dfrac{d}{dx} tan(x)$

Derivative of $tan(x) = sec^{2}x$. Hence,

$\dfrac{d}{dx} (1 + tan^{2}x) = 2. tanx. sec^{2}x$

Hence, the derivative of $(1+ tan^{2}x)$ is equal to $sec^{2}x$.

Practice Questions:

1. Determine the derivative of $(sec^{2}x)^{2}$ with respect to x.
2. Determine the derivative of $sec^{2}x^{2}$ with respect to $x^{2}$.

Answer Key:

1).

$\dfrac{d}{dx}(sec^{2}x)^{2} = (2. sec^{2}x)^{2-1}. \dfrac{d}{dx} sec^{2}x$

$\dfrac{d}{dx}(sec^{2}x)^{2} = (2. sec^{2}x). \dfrac{d}{dx} sec^{2}x$

$\dfrac{d}{dx}(sec^{2}x)^{2} = (2. sec^{2}x). 2.secx . \dfrac{d}{dx} secx$

$\dfrac{d}{dx}(sec^{2}x)^{2} = 2. sec^{2}x. 2.secx . secx .tanx$

$\dfrac{d}{dx}(sec^{2}x)^{2} = 4. sec^{4}x .tanx$

2).

We can determine the derivative of $sec^{2}x^{2}$ by the combination of the chain rule and substitution method. The chain method will be used to determine the derivative, while the substitution method will help us to calculate the derivative with respect to variable $x^{2}$.

Let us assume that $a = sec^{2}x^{2}$ while $b = x^{2}$.

$\dfrac{da}{dx} = \dfrac{d}{dx} sec^{2}x^{2}$

$\dfrac{da}{dx} = 2 sec x^{2}. sec x^{2}. tan x^{2}.2x$

$\dfrac{da}{dx} = 4x. sec^{2}x^{2}.tan x^{2}$

$\dfrac{db}{dx} = \dfrac{d}{dx} x^{2} = 2x$

$\dfrac{da}{db}$ = $\dfrac{d sec^{2} .x^{2}}{x^{2}}$ so by doing this we will get the derivative of the function with respect to $x^{2}$

$\dfrac{d sec^{2}x^{2}}{x^{2}} = \dfrac {4x. sec^{2}x^{2}.tan x^{2}} {2x}$

$\dfrac{d sec^{2}x^{2}} {x^{2}} = 2. sec^{2}x^{2}.tan x^{2}$

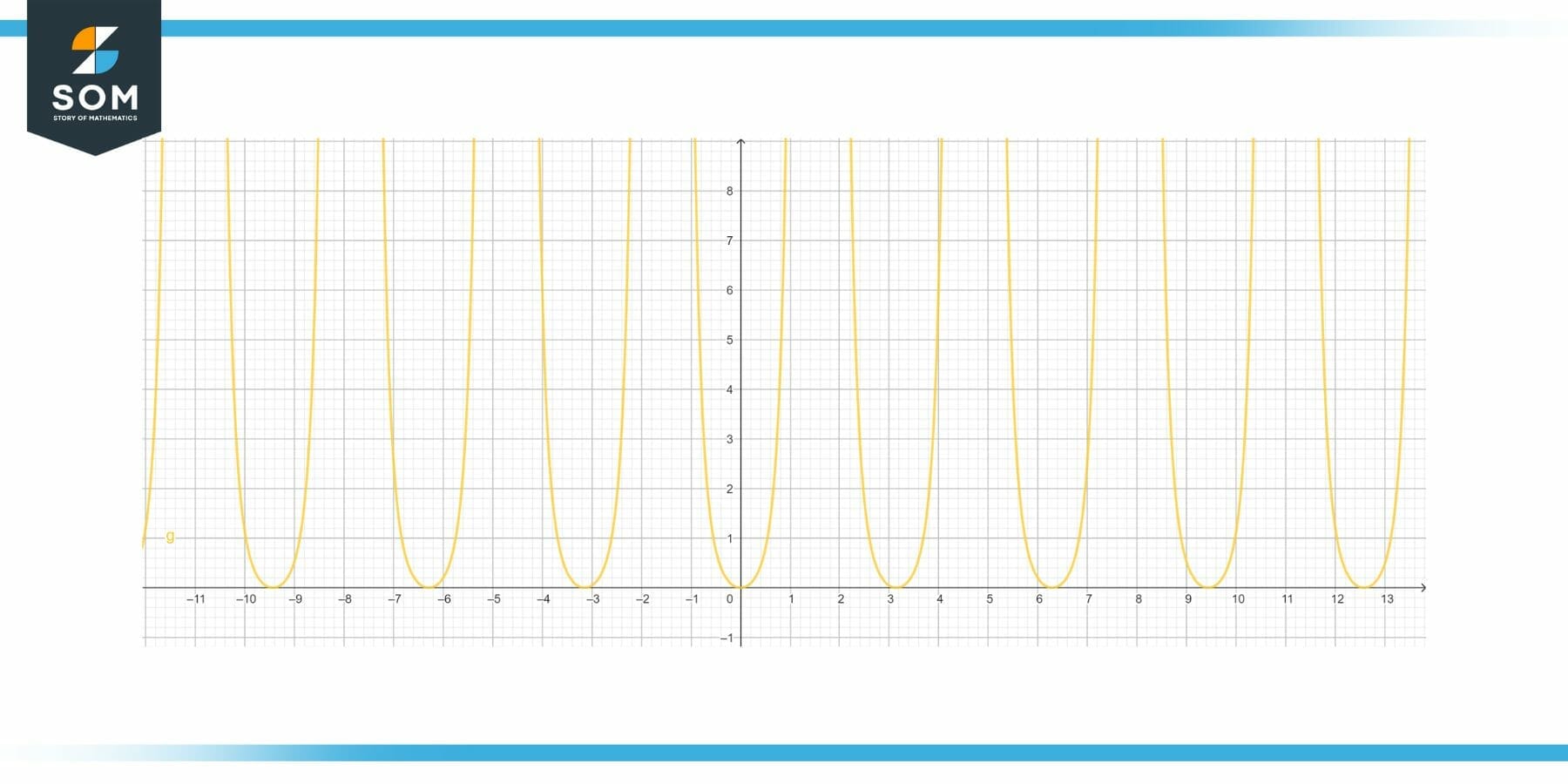
Hence, the derivative of $sec^{2}x^{2}$ with respect to $x^{2}$ is $2. sec^{2}x^{2}.tan x^{2}$. The graph of the derivative of $sec^{2}x^{2}$ is shown below.

Important Notes/ Other Formulas

1. Derivative of sec^2(x)tan(x) =
2. Derivative of sec^3x =
3. The second derivative of sec^2x =
4. Derivative of 2 sec^2x tan x