JUMP TO TOPIC
A square degree, that is deg$^2$, is a non-SI unit of solid angle measurement. Square degrees are utilized to quantify components of a sphere in the same way that degrees are utilized to quantify components of a circle. In this complete guide, you will get to know about the degree, the square degree, and circles as well as spheres.
What Is a Square Degree?
In a similar way that one degree is equal to $\dfrac{\pi}{180}$ radians, a square degree is equal to $\left(\dfrac{\pi}{180}\right)^2$ steradians or sr, or approximately $1/3283=3.046\times 10^{-4}$ sr. The whole sphere has a solid angle of $4\pi$ sr, or approximately $41253$ deg$^2$.
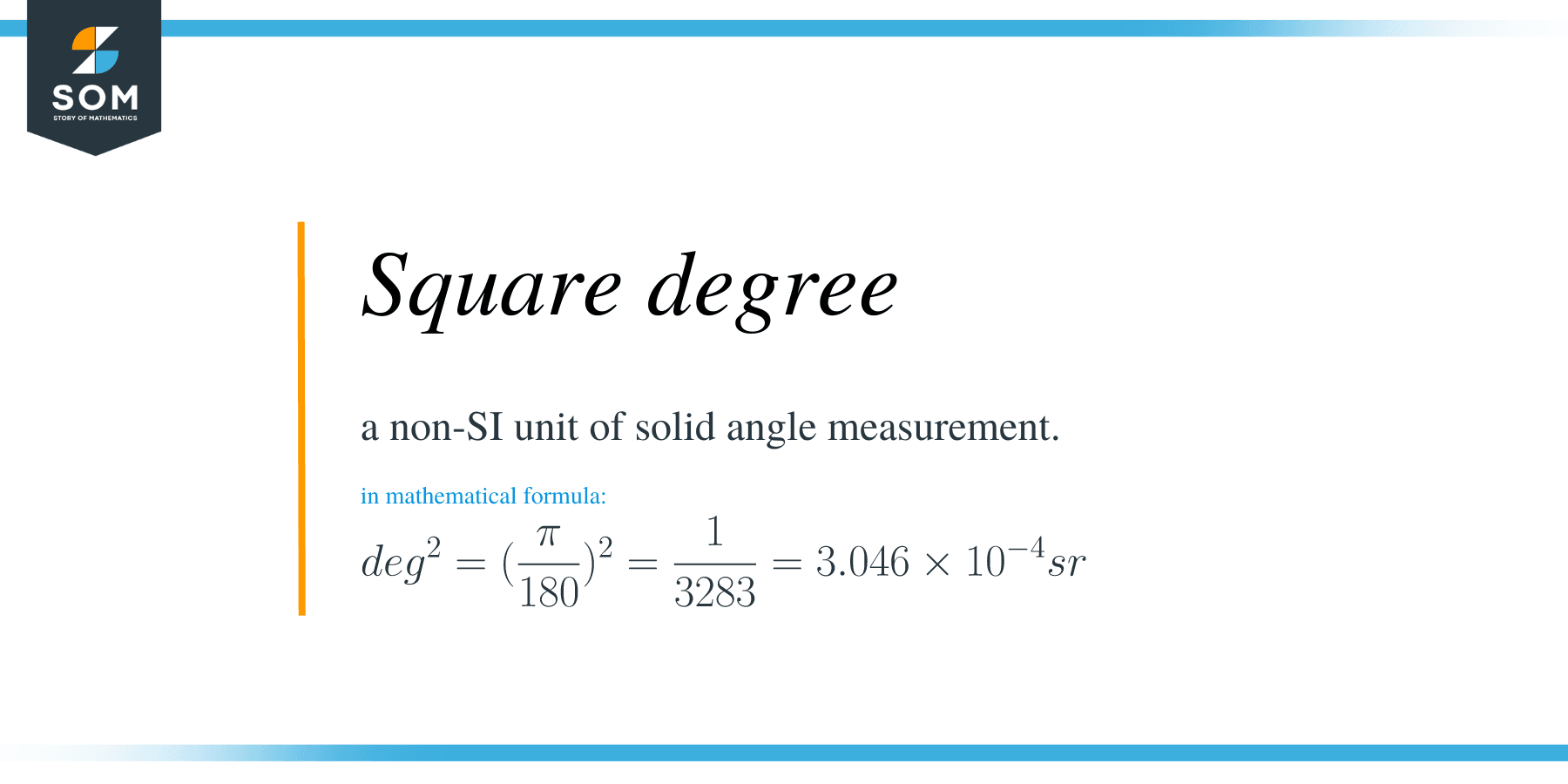
Degree
A degree, also known as an arc degree, degree of arc, or arcdegree, is commonly represented by the symbol $°$, which is a measurement of a plane angle wherein the one full rotation is $360$ degrees.
It is not a SI unit since the SI unit of angular measure is regarded as the radian, although it is listed as an acknowledged unit in the SI brochure. Since a full rotation equals two radians, one degree is equal to $\dfrac{\pi}{180}$ radians.
Example
When seen from the Earth’s surface, the full moon encompasses only around $0.2$ deg$^2$ of the sky. The Sun is approximately half a degree across (similar to the full moon) and encompasses only $0.2$ deg$^2$ when viewed from Earth.
Radian
The radian, represented by the symbol rad, is the International System of Units (SI) unit of angle and the standard unit of angular measurement utilized in numerous mathematical disciplines. Previously, the unit was a SI supplementary unit. The SI defines the radian as a dimensionless unit of $1$ rad $= 1$. As a result, its symbol is frequently omitted, particularly in mathematical writing.
One radian is described as the angle formed by the center of a circle intersecting an arc of length that is equivalent to the radius of the circle. In a broad sense, the magnitude of a subtended angle in radians equals the ratio of the arc length and the radius of the circle.
Steradian
In the International System of Units, the steradian symbol sr (square radian) is the unit of solid angle. It is utilized in three-dimensional geometry and is similar to the radian, which is employed to quantify planar angles. A solid angle in steradians projected upon a sphere provides an area on the surface, whereas an angle in radians projected onto a circle provides a length on the circumference of a circle.
Similar to the radian, the steradian is a dimensionless unit that is defined as the quotient of the area subtended and the square of its distance from the center.
This ratio’s numerator and denominator both include the dimension length squared. Moreover, it is important to differentiate between dimensionless quantities of various types, so the symbol sr is utilized to represent a solid angle.
Plane Angle
Two straight lines intersecting at a point describe a plane angle. The plane angle is the distance between such lines in the plane characterized by them. It also is expressed in degrees or radians with $2\pi$ radians in a circle or $360$ degrees to a circle.
It is highlighted in preparation for identifying a solid angle that the plane angle could also be expressed in terms of the radial projection of a line segment in a plane onto a point.
Solid Angle
The solid angle extends the plane angle idea to the surface of a sphere. An angle with a value equivalent to the area on a sphere occupied by a surface divided by the square of that sphere’s radius. Such angles are measured in steradians.
A three-dimensional angle is formed by the intersection of three or even more planes at one point. The steradian is used to measure the magnitude of such angles where steradian is a dimensionless quantity.
The corner of a room, like the apex of a cone, shapes a solid angle. You can assume an infinite number of planes establishing the smooth round surface of the cone, all having the common intersection point, that is, the apex.
In photometry, solid angles are frequently utilized. All standard sections of a cone at the vertex have equal solid angles, and because their attractions on a particle at the vertex are proportional to their distances from the vertex, they are numerically equal to one another as well as to the solid angle of the cone.
What Is a Circle?
A circle is a certain type of ellipse where the eccentricity is $0$ and it has two coincident foci. A circle is also referred to as the locus of points drawn at an equal distance from the center.
The radius of a circle is known as the distance between its center and its exterior line. The diameter of a circle is known as the line that divides it into two equal parts and is equivalent to twice the radius.
A circle is a basic two-dimensional figure that is measured by its radius. The circle simply split the plane into two sections, that is exterior and interior. It is comparable to a line segment. Assume the line segment is bent through until its ends meet. Organize the loop so that it is perfectly circular.
Since the circle is a 2D shape with an area and a perimeter, the circle’s perimeter, also known as its circumference, is the distance all around the circle. In a two – dimensional plane, the area of a circle is the region confined by it.
A circle is one of the most basic shapes that is introduced early in education. This is because circles are easy to identify and are not as complex as other shapes.
What Is a Sphere?
A sphere is a three-dimensional object with a circular shape. The sphere is divided into three axes, which are the $x-$axis, the $y-$axis, and the $z-$axis. This is the primary distinction between a circle and a sphere. A sphere, unlike other 3D shapes such as pyramids or cubes, has no vertices or edges.
The points on the sphere’s surface are equally distant from the center. As a result, the distance between the sphere’s center and the surface is the same at any point. Its radius is the length of this distance.
Examples of spheres include a globe, a soccer ball, the planets, etc. The surface area of one whole sphere is the overall area surrounded by a sphere’s surface in three dimensions. The formula for surface area is known to be $4\pi r^2$ square units.
Conclusion
This guide has explained in detail the concepts of degrees, square degrees, circles, and spheres, so to gain a better understanding of the study, let us summarize the concepts presented:
- A square degree denoted by deg$^2$ is a non-SI unit of solid angle measurement.
- A degree is a plane angle measurement in which one full rotation equals 360 degrees.
- Square degrees are utilized to measure the components of a sphere.
- Solid angles are measured in steradians.
- A square degree is equal to $\left(\dfrac{\pi}{180}\right)^2$ steradians (sr).
A square degree is a non-SI unit of measurement used to measure the parts of a sphere and is equal to $\left(\dfrac{\pi}{180}\right)^2$ steradians (sr). Similar to how radians can be converted to degrees and vice versa, steradians can be converted to square degrees and vice versa.
A lot of problems in mathematics and physics make use of degrees and square degrees, so why not put some difficult problems to the test and become an expert at converting square degrees to steradian and vice versa?