
Immerse yourself in the captivating world of linear algebra as we explore the concept of projection of u onto vector v. Projecting vectors is akin to casting a shadow, capturing the essence of one entity onto another.
Through this article, we will unfold the layers of this intriguing mathematical operation, walking you through the theory behind projections, calculations, and applications.
Defining Projection of u onto v
In vector algebra, the projection of vector u onto vector v, often denoted as proj_v(u), is a vector operation that creates a new vector which is the shadow or projection of u onto v. This resulting vector is parallel to v and is the closest approximation of u in the direction of v.
Mathematically, if u and v are vectors in an inner-product space and v ≠ 0, then the projection of u onto v is given by:
proj_v(u) = ((u•v) / ||v||²) * v
where:
- u•v represents the dot product of u and v
- ||v|| represents the magnitude of vector v
This formula can be understood as the scaling of vector v by the factor of how much of u is in the direction of v.
In simpler terms, if you imagine standing in a field and casting a shadow by the light of the sun, the shadow is a “projection” of you onto the ground. In the same way, the projection of u onto v gives the “shadow” of u if v is imagined as the ground.
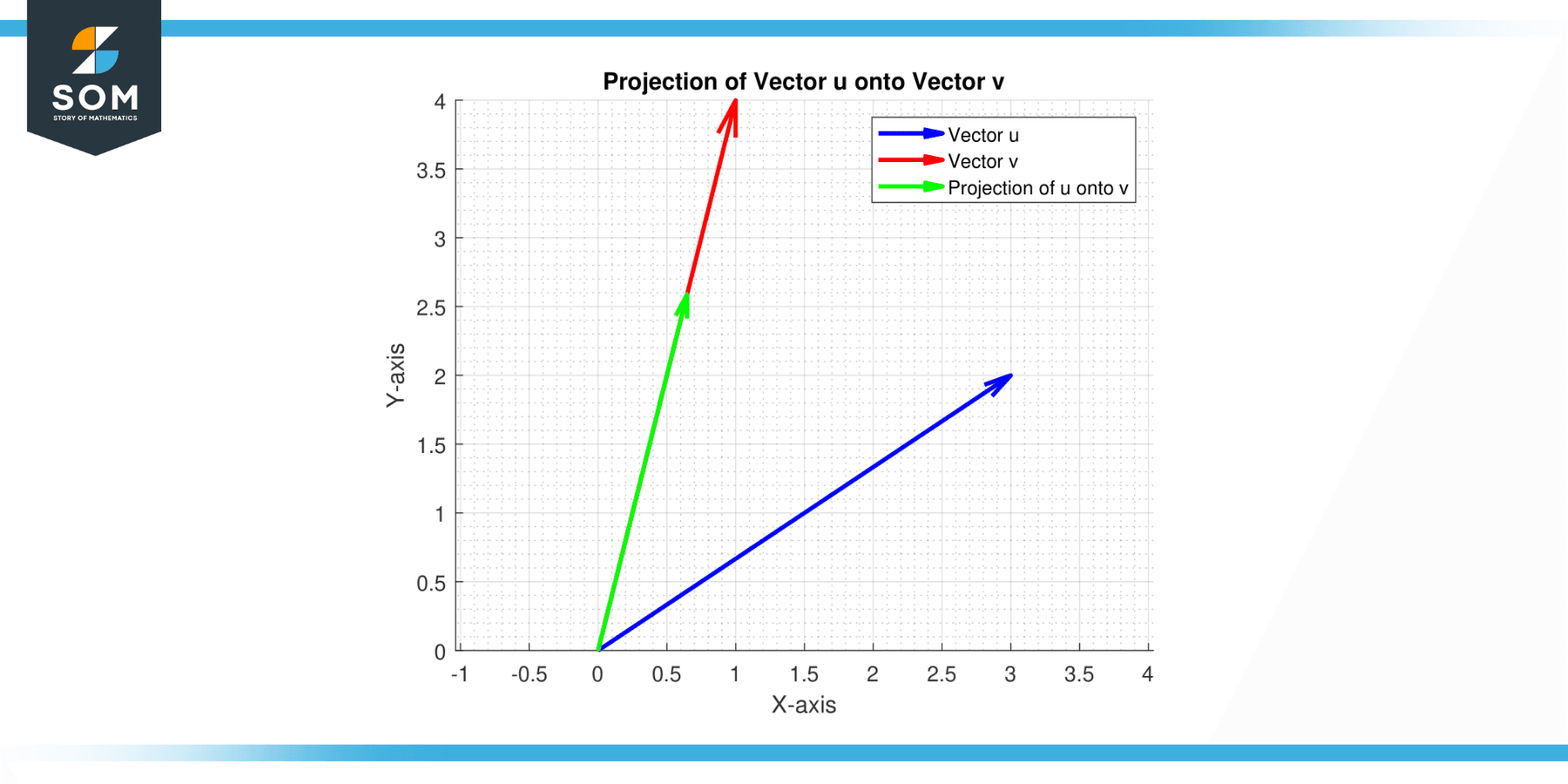
Figure-1.
Properties
Parallelism
The projection of vector u onto vector v is a vector that is parallel to v. This makes sense when considering the physical analogy of a shadow: when you project (cast a shadow of) an object onto a surface, the shadow lies on the surface.
Scalar Multiplication
If you multiply a vector u by a scalar k, the projection of the resulting vector ku onto v is equal to the scalar k times the projection of u onto v. This is written as proj_v(ku) = k * proj_v(u).
Dot Product Basis
Indeed, the projection operation is based on the dot product of vectors. The dot product measures the extent to which one vector extends in the direction of another, which is essentially what we’re trying to find when we calculate a projection.
Length
The length (or magnitude) of the projection of u onto v is always less than or equal to the length of u. It will only be equal if u and v are pointing in the exact same (or exactly opposite) directions.
Orthogonality
The difference between the original vector u and its projection onto v is orthogonal (perpendicular) to v. This means that if u – proj_v(u) = w, then w · v = 0 (where · represents the dot product).
Additivity
The projection operation does not generally distribute over addition. That is, proj_v(u1 + u2) is not necessarily equal to proj_v(u1) + proj_v(u2).
Zero Vector
The projection of the zero vector onto any vector is the zero vector. That is, proj_v(0) = 0.
Null Projection
The projection of any vector onto the zero vector is undefined, since the operation involves division by the magnitude of the vector v, and the magnitude of the zero vector is 0.
Exercise
Example 1
Let’s say we have vectors u = (3, 4) and v = (1, 0). We want to project u onto v.
Solution
The formula for projection is:
proj_v(u) = ((u⋅v) / ‖v‖²) * v
First, compute the dot product u⋅v = (31 + 40) = 3. Next, compute the magnitude of v squared:
‖v‖² = (1² + 0²) = 1
So, the projection of u onto v is (3/1)*(1,0) = (3, 0).
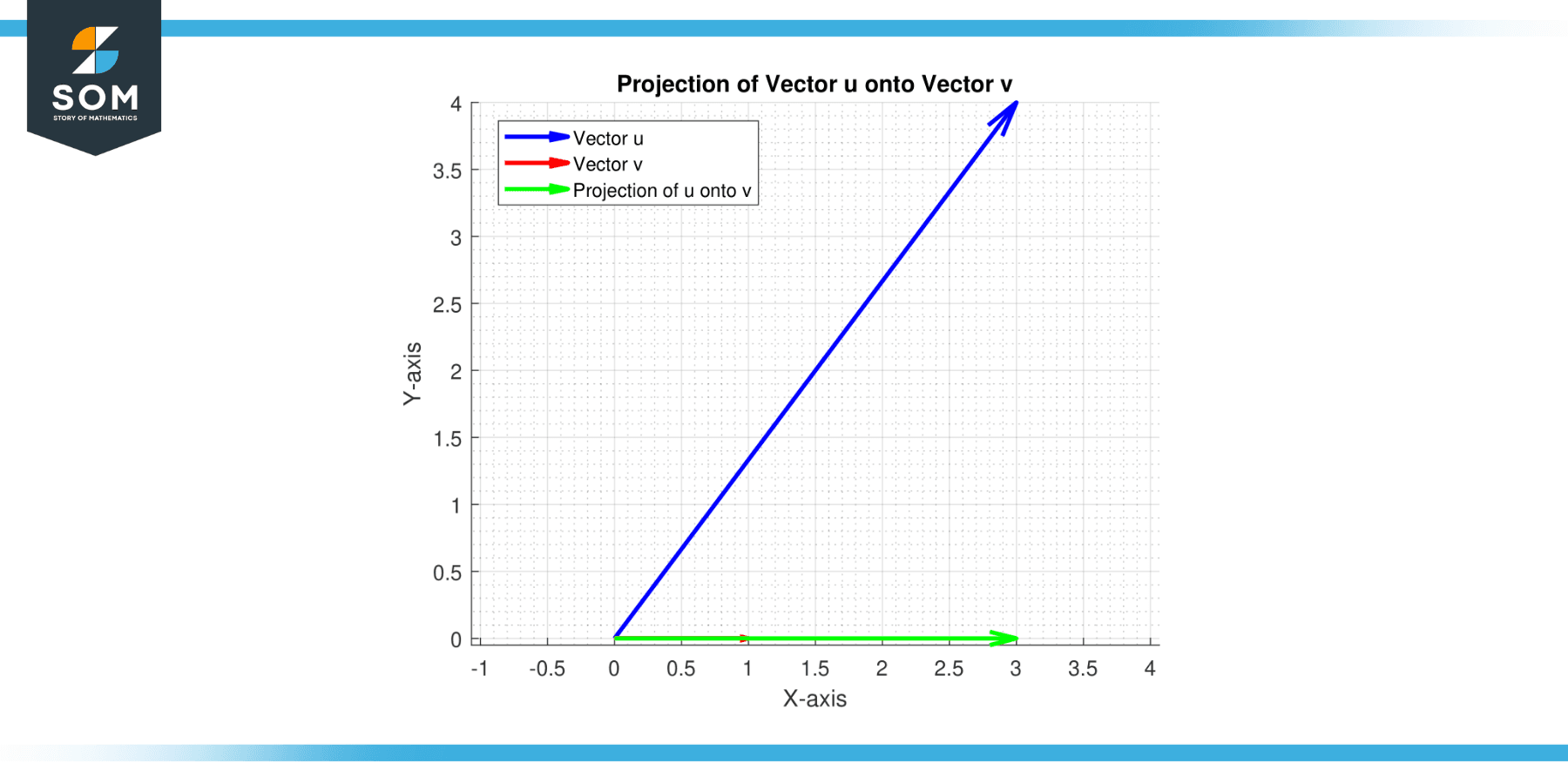
Figure-2.
Example 2
Let’s say we have vectors u = (1, 2, 3) and v = (2, 2, 2). We want to project u onto v.
Solution
First, compute the dot product u⋅v = (12 + 22 + 32) = 12.
Next, compute the magnitude of v squared:
‖v‖² = (2² + 2² + 2²) = 12
So, the projection of u onto v is (12/12)(2,2,2) = (2, 2, 2).
Example 3
Let’s say we have vectors u = (3, 1) and v = (-1, 2). We want to project u onto v.
Solution
First, compute the dot product u⋅v = (3*-1 + 12) = -1.
Next, compute the magnitude of v squared:
‖v‖² = ((-1)² + 2²) = 5
So, the projection of u onto v is ((-1)/5)(-1,2) = (1/5, -2/5).
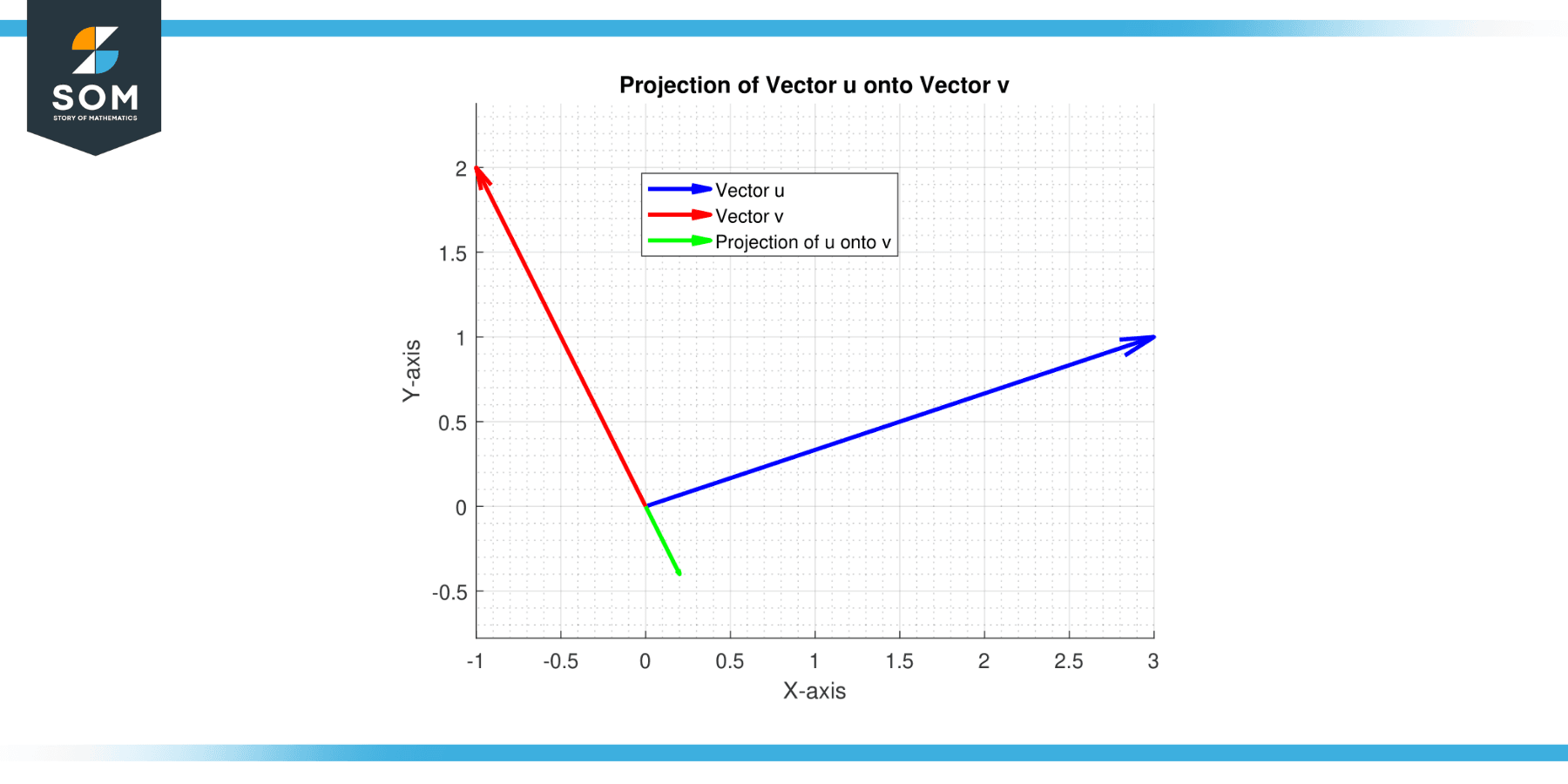
Figure-3.
Applications
Computer Graphics
Vector projections are used extensively in computer graphics and game development.
For instance, to calculate lighting in 3D graphics, vector projection can be used to determine how much light from a light source hits a surface based on the angle between the light direction and the surface normal (a vector perpendicular to the surface).
Machine Learning
In machine learning, projection is used in dimensionality reduction techniques, such as Principal Component Analysis (PCA). PCA projects data onto the axes (principal components) that represent the most variance in the data, reducing the number of dimensions while preserving as much information as possible.
Computer Vision
Vector projections play a key role in feature matching and image stitching in computer vision. They are used in algorithms that find correspondences between different views of a 3D scene taken from different viewpoints.
Statistics and Data Analysis
In statistics, vector projections can be used to calculate the regression line in linear regression. The best-fit line is found by projecting the data points onto a line in a way that minimizes the distance (usually squared distance) between the data points and their projections.
Geography and Geographic Information Systems (GIS)
Vector projections are used to project geographical data from the 3D surface of the Earth onto a 2D map while preserving certain properties like area or angles.
Signal Processing
In signal processing, projections are used to decompose signals into components. For example, the Fourier transform decomposes a signal into sinusoidal components, and this can be viewed as projecting the signal onto a set of basis functions.
All images were created with GeoGebra.
