JUMP TO TOPIC
The Descartes Rule of Signs is a technique used in polynomials to determine the number of positive and negative real roots. It makes use of the signs of the coefficients of the terms of the polynomial by counting the times of change in signs of the coefficients. This technique is important in locating the real roots of the polynomial, thus making it easier to describe the behavior of the graph.
In this article, we will learn how to use Descartes rule of signs in describing the real roots of a polynomial and apply this to some examples with detailed solutions and explanations.
What Is Descartes Rule of Signs?
The Descartes rule of signs is a method devised by René Descartes to determine the possible number of positive and negative real zeroes of a polynomial. This technique focuses on counting the number of changes in signs of the coefficients of the polynomial function $f(x)$ and $f(-x)$ to determine the highest possible number of positive and negative real roots.
Advantage of Using This Method
A polynomial function with degree $n$ expressed as:
\begin{align*}
f(x)=a_n x^n+a_{n-1} x^{n-1}+\dots+a_2 x^2+a_1 x+a_0
\end{align*}
has at most $n$ real roots. However, using Descartes Rule of Signs, just by looking at the polynomial, we could determine right away how many of these real roots can be positive and how many of them can be negative.
The advantage of using the Descartes rule of signs is that we can easily find out the possible number of real roots that are positive and negative without graphing the polynomial function or manually solving for the roots of the polynomial. Since the zeroes of the graph are the points in the graph that are located on the x-axis, the Descartes rule of signs lets us know how many times the graph touches the left x-axis and the right x-axis.
For example, the graph of the polynomial function $f(x)=x^6+5x^5-3x^4-29x^3+2x^2+24x$ is shown in Figure 1.
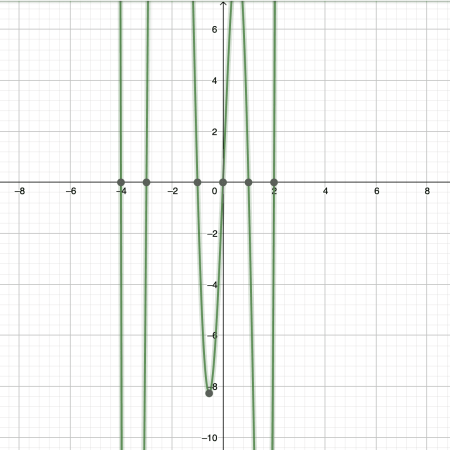
The graph shows that the roots of the given polynomial are located at the points $(-4,0)$, $(-3,0)$, $(-1,0)$, $(0,0)$, $(1,0)$, and $(2,0)$. This means that the polynomial has two positive roots and three negative roots since the root in the origin is neither positive nor negative. But with the Descartes rule of signs, we can determine these numbers right away without graphing the polynomial.
Continue reading the following section to learn how to use this method.
How To Use Descartes Rule of Signs
To use the Descartes rule of signs, you must first make sure that the order of the terms of the polynomial function follows this form:
\begin{align*}
f(x)= a_n x^n+a_{n-1} x^{n-1}+\dots+a_2 x^2+a_1 x+a_0.
\end{align*}
That is, the terms are arranged in a descending order based on the degree or exponent of each term.
Next, count the number of changes from positive $(+)$ to negative $(–)$, and negative $(–)$ to positive $(+)$. Suppose there are $p$ transitions in the signs of the coefficients, then the polynomial has at most $p$ positive real roots.
- If $p$ is an even number, then the possible number of positive real roots are all the even numbers less than or equal to $p$.
- If $p$ is odd, then the possible number of positive real roots are all the odd numbers less than or equal to $p$.
For example, if $p=4$, then the polynomial has at most four positive real roots. Moreover, the polynomial either has four, two, or no positive real roots. Similarly, if $p=5$, then the polynomial has at most five positive real roots, and the polynomial either has five, three, or one negative real root.
After that, to determine the possible number of negative real roots, we change x to -x in the polynomial function and express the function $f(-x)$.
\begin{align*}
f(-x)=a_n (-x)^n+a_{n-1} (-x)^{n-1}+⋯+a_2 (-x)^2+a_1 (-x)+a_0
\end{align*}
Then, we follow the similar steps we have shown in finding the possible number of positive real roots. We count the number of transitions in the signs of the coefficients of the terms of the function $f(-x)$. If there are $q$ transitions of signs of the coefficients, then the polynomial has at most $q$ negative real roots.
- If $q$ is an even number, then the possible number of negative real roots are all the even numbers less than or equal to $q$.
- If $q$ is odd, then the possible number of negative real roots are all the odd numbers less than or equal to $q$.
Take note that the possible number is dependent on the number of transitions of the signs, so count carefully. This indicates whether there is an even number or an odd number of positive and negative real roots.
Look at the following examples to know how to apply Descartes rule of signs in a given polynomial function.
Example 1
- Find the highest possible number of positive and negative real roots of the polynomial
\begin{align*}
f(x)=x^6+5x^5-3x^4-29x^3+2x^2+24x.
\end{align*}
The terms of the polynomial are already arranged in the order that we need, so we can proceed to highlighting the signs of the coefficients (blue for positive and green for negative).
$+x^6+5x^5$$-3x^4-29x^3$$+2x^2+24x$
Note that there are only two transitions in signs of the coefficients of the terms, from:
$+5x^5$ to $-3x^4$ (positive to negative), and
$-29x^2$ to $2x^2$ (negative to positive).
Thus, the polynomial function has at most two positive real roots. Moreover, the function has two or no positive real roots.
We solve for $f(-x)$.
\begin{align*}
f(-x)&=(-x)^6+5(-x)^5-3(-x)^4-29(-x)^3+2(-x)^2+24(-x)\\
&=(x^6 )+5(-x^5 )-3(x^4 )-29 (-x^3 )+2(x^2 )+24 (-x)\\
&=+x^6-5x^5-3x^4+29x^3+2x^2-24x
\end{align*}
Then, we have:
$+x^6$$-5x^5-3x^4$$+29x^3+2x^2$$-24x$
Note that there are three transitions in signs, which are:
$+x^6$ to $-5x^5$,
$-3x^4$ to $+29x^3$, and
$+2x^2$ to $-24x$.
This implies that there are at most three negative real roots. The polynomial has one or three negative real roots.
Answer: The polynomial function has at most two positive real roots and at most three negative real roots. Moreover, it has two or no positive real roots and one or three negative real roots.
Take note that this is the polynomial function we graphed earlier and located its roots in the graph. We can verify that the results we obtained using the Descartes rule of signs are correct because the polynomial has two positive real roots and three negative real roots.
Example 2
- Describe the roots of the function:
\begin{align*}
f(x)=17x-x^2-x^3-15.
\end{align*}
We arrange the terms of the polynomial in descending order of exponents.
\begin{align*}
f(x)=-x^3-x^2+17x-15
\end{align*}
Then, we highlight the terms based on the sign of their coefficient.
$-x^3-x^2$$+17x$$-15$
There are two transitions in signs from $-x^2$ to $+17x$, then to $-15$. Therefore, the function has at most two positive real roots. Then, it has either two or no positive real roots.
Next, we look for the expression of $f(-x)$.
\begin{align*}
f(-x)&= -(-x)^3-(-x)^2+17(-x)-15\\
&=+x^3-x^2-17x-15\\
\end{align*}
So, we have:
$+x^3$$-x^2-17x-15$
Since the first term is the only one with positive coefficients and all the following terms have negative coefficients, their signs changed only once in the expression. The function has at most one negative real root. However, since $1$ is odd, then it is not possible for the polynomial to have zero negative real roots. Thus, the polynomial has exactly one negative real root.
Answer: The polynomial function has exactly one negative real root and has two or no positive real roots.
Example 3
- How many possible positive and negative real roots does
\begin{align*}
f(x)=x^3+x-3x^2-3?
\end{align*}
Arranging the terms in the function, we have:
\begin{align*}
f(x)=x^3-3x^2+x-3.
\end{align*}
We count the number of changes in the signs of the coefficients.
$+x^3$$-3x^2$$+x$$-3$
There are three transitions in signs in the polynomial expression. Thus, there are at most three positive real roots. The function has one or three positive real roots.
We now solve for f(-x).
\begin{align*}
f(-x)&=(-x)^3-3(-x)^2+(-x)-3\\
&=-x^3-3x^2-x-3
\end{align*}
We take note of the change in signs.
$-x^3-3x^2-x-3$
Note that all the terms of $f(-x)$ are negative. Thus, there is no change in signs between terms. Hence, the polynomial has no negative real roots.
Answer: The function has no negative real roots and has one or three positive real roots.
Let’s verify the results we obtained using the Descartes rule of signs.
Note that if we factor the polynomial $x^3-3x^2+x-3$, we have:
\begin{align*}
x^3-3x^2+x-3&=(x^3-3x^2 )+(x-3)\\
&=x^2 (x-3)+(x-3)\\
&=(x^2+1)(x-3)
\end{align*}
The polynomial has exactly one real root, $x=3$, which is positive. The factor $x^2+1$ has no real roots. Therefore, the polynomial has one positive real root and no negative real roots. The conclusion we derived here agrees with the results we get using Descartes rule of signs.
FAQ
Is Descartes Rule of Signs Important?
Yes, the Descartes rule of signs is important because this gives us a description of the polynomial in terms of quantity and signs of its real roots. This technique also serves as a shortcut in determining the possible number of positive and negative real roots without going through the tedious task of factoring or graphing the polynomial to determine the signs of the real roots.
How Do You Use Descartes Rule of Signs To Determine the Possible Number of Positive and Negative Real Zeros?
To do this, you can count the number of transitions in signs of the coefficients of the terms of $f(x)$ (for positive real roots) and $f(-x)$ (for negative real roots). The number of transitions obtained in $f(x)$ and is the maximum number of positive and negative real roots, respectively. If the number of transitions is even, then the number of positive or negative real roots is also even. Similarly, if there is an odd number of transitions, then the possible number of positive or real roots is also odd.
How Do You Determine Positive and Negative Roots?
Positive and negative roots are determined by factoring the polynomial or finding values of $x$ such that $f(x)=0$. The Descartes rule of signs does not determine the values of the positive and negative roots of a polynomial. It only determines the possible number of positive and negative real roots.
Conclusion
The Descartes rule of signs is a very useful technique in describing the real roots of a polynomial, and it is the easiest way to know the possible number of positive and negative real roots. Since a polynomial of degree $n$ has at most $n$ real roots, then using this method also helps us determine whether the polynomial has roots equal to zero or has imaginary roots by checking whether the sum of the highest number of positive and negative real roots is less than $n$.
- The Descartes rule of signs is used in determining the possible number of positive and negative roots of a polynomial function $f(x)$. If $p$ is the number of transitions in the signs of the terms of $f(x)$, then the polynomial has at most $p$ positive real roots.
- The possible number of positive real roots are the even numbers less than or equal to $p$ if $p$ is even, and the possible number of positive real roots are the odd numbers less than or equal to $p$ if $p$ is odd.
- If $q$ is the number of transitions in the signs of the terms of $f(-x)$, then the polynomial has at most $q$ negative real roots.
- The possible number of negative real roots are the even numbers less than or equal to $q$ if $q$ is even, and the possible number of negative real roots are the odd numbers less than or equal to $q$ if $q$ is odd.
- The Descartes rule of signs does not determine the value of the positive and negative real roots of the polynomial.
Even though the Descartes rule of signs does not give us the values of the real roots of the polynomial, it is still an essential tool in root-finding problems. Knowing the possible number of positive and negative real roots allows us to reduce the number of possible solutions that we need to consider, thus saving us some time.