
This article aims to take you on an immersive journey into the realm of direction cosines. We’ll unearth their definition, properties, and significant applications in various fields, revealing their profound impact on our comprehension and manipulation of multi-dimensional spaces.
Definition of Direction Cosines
In mathematics, particularly in vector calculus and physics, direction cosines are three coefficients used to represent a vector’s orientation in three-dimensional space. They are called “cosines” because they are the cosines of the vector’s angles with each coordinate axis.
Given a vector in 3-dimensional space, it will form an angle with each of the coordinate axes (x, y, and z). If we denote these angles as α (with the x-axis), β (with the y-axis), and γ (with the z-axis), then the direction cosines are:
l = cos(α), m = cos(β), n = cos(γ)
These three quantities – l, m, and n – give us a way to define the direction of the vector. They are particularly useful because they provide a normalized (i.e., scale-independent) way to specify a vector’s direction.
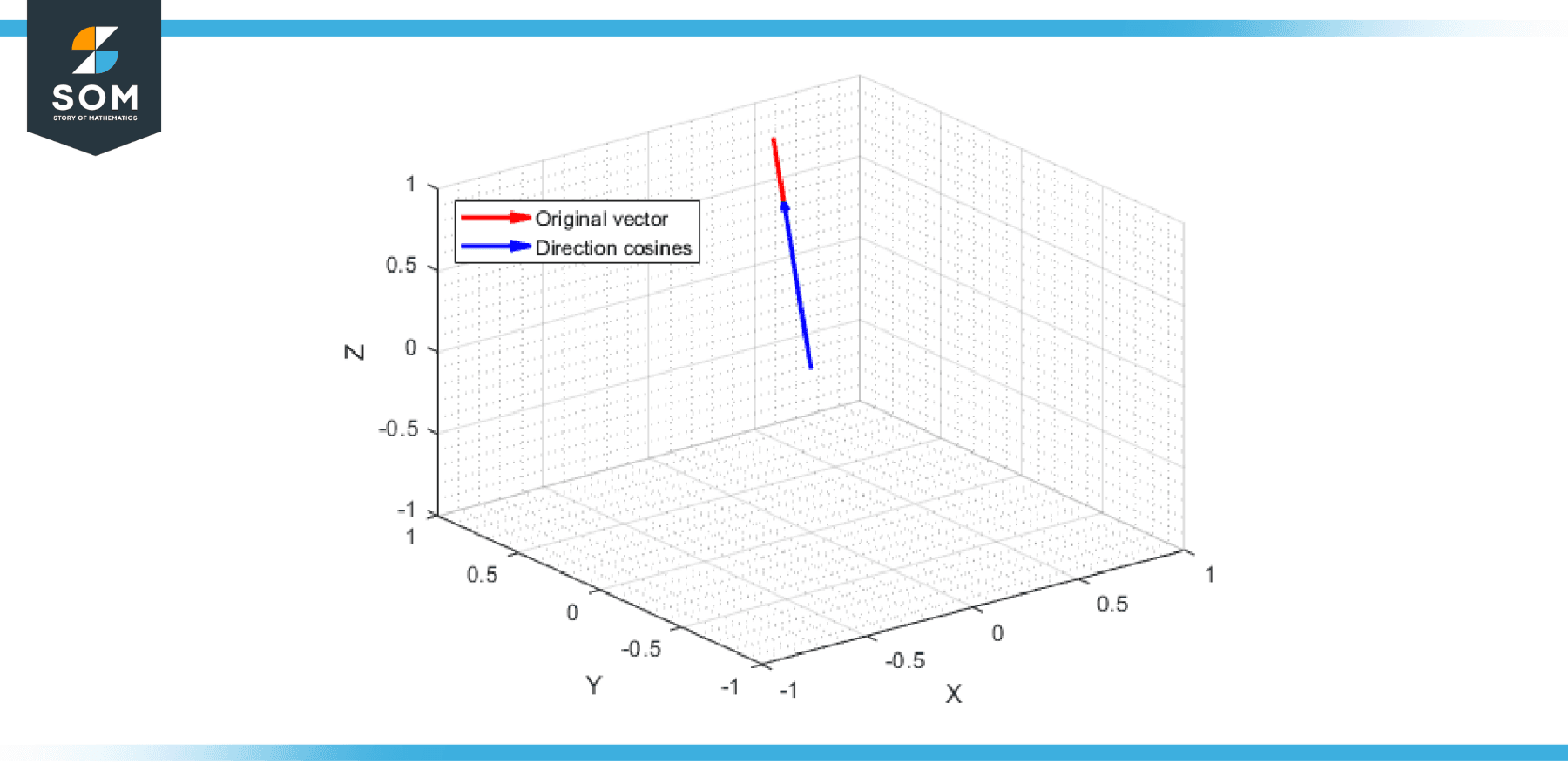
Figure-1.
It’s worth noting that direction cosines obey an important relationship known as the direction cosine rule, which states that l² + m² + n² = 1. This relationship results from the geometric interpretation of the dot product and the definition of the cosine function.
Properties
Direction cosines offer a clear way to understand the orientation of a vector in three-dimensional space. Here are the key properties associated with direction cosines:
Normalization
The squares of the direction cosines (l, m, n) always add up to 1, no matter the vector’s orientation. This is stated mathematically as l² + m² + n² = 1. This property comes from the fact that the direction cosines are defined based on the unit vector in the direction of the given vector, and the length of a unit vector is always 1.
Independence of Length
Direction cosines are independent of the length (magnitude) of the vector. They solely depend on the direction of the vector. Hence, two vectors that are parallel (or anti-parallel) to each other will have the same (or negative of each other’s) direction cosines, irrespective of their magnitudes.
Orientation With Axes
The direction cosine corresponding to an axis gives the cosine of the angle the vector makes with that axis. For instance, l, the direction cosine corresponding to the x-axis, is the cosine of the angle between the vector and the x-axis.
Connection to Direction Ratios
Direction cosines are related to the direction ratios of a vector. If a vector’s direction ratios (A, B, C) are known (direction ratios are simply the proportions of the x, y, and z components of the vector), the direction cosines (l, m, n) can be found as l = A/r, m = B/r, n = C/r, where r is the magnitude of the vector, i.e., √(A² + B² + C²).
Basis for Rotation Matrices
In three dimensions, any rotation can be defined by an axis of rotation and an angle to rotate. The cosines of the angles between this axis and the coordinate axes (the direction cosines of the axis of rotation) form the basis of the rotation matrix that represents this rotation.
Remember, when working with direction cosines, you must ensure that the vector for which you’re finding the direction cosines is not the zero vector (as its direction is undefined), and that all angles and computations follow the conventions of the coordinate system you’re working in (typically a right-handed Cartesian coordinate system).
Ralevent Formulas
Direction cosines are linked with several mathematical concepts and formulas, primarily related to the orientation and transformation of vectors in three-dimensional space. Here’s a deeper look at some of the most important formulas:
Normalization Condition
Due to the geometric and trigonometric properties of the cosines of the angles and the Euclidean norm (length) of a vector, the direction cosines always satisfy the following relation:
l² + m² + n² = 1
Direction Ratios and Magnitude of Vector
If A, B, and C are the direction ratios (proportions of the x, y, and z components of the vector) and r is the magnitude of the vector, then the direction cosines can be calculated as:
l = A/r
m = B/r
n = C/r
where r = √(A² + B² + C²).
Conversion Between Direction Cosines and Angles
Since direction cosines are just the cosines of the angles between the vector and the coordinate axes, we can convert between them using the inverse cosine (arccos or cos⁻¹) function:
α = cos⁻¹(l)
β = cos⁻¹(m)
γ = cos⁻¹(n)
Dot Product and Angle Between Vectors
The dot product of two vectors is also connected with direction cosines. If you have two vectors with direction cosines (l₁, m₁, n₁) and (l₂, m₂, n₂), then the cosine of the angle θ between them is given by:
cos(θ) = l₁l₂ + m₁m₂ + n₁n₂
Exercise
Example 1
Determine the direction cosines for the vector having angles α = 0, β = 0, γ = 0 with the coordinate axes
Solution
The direction cosines are:
l = cos(0) = 1
m = cos(0) = 1
n = cos(0) = 1
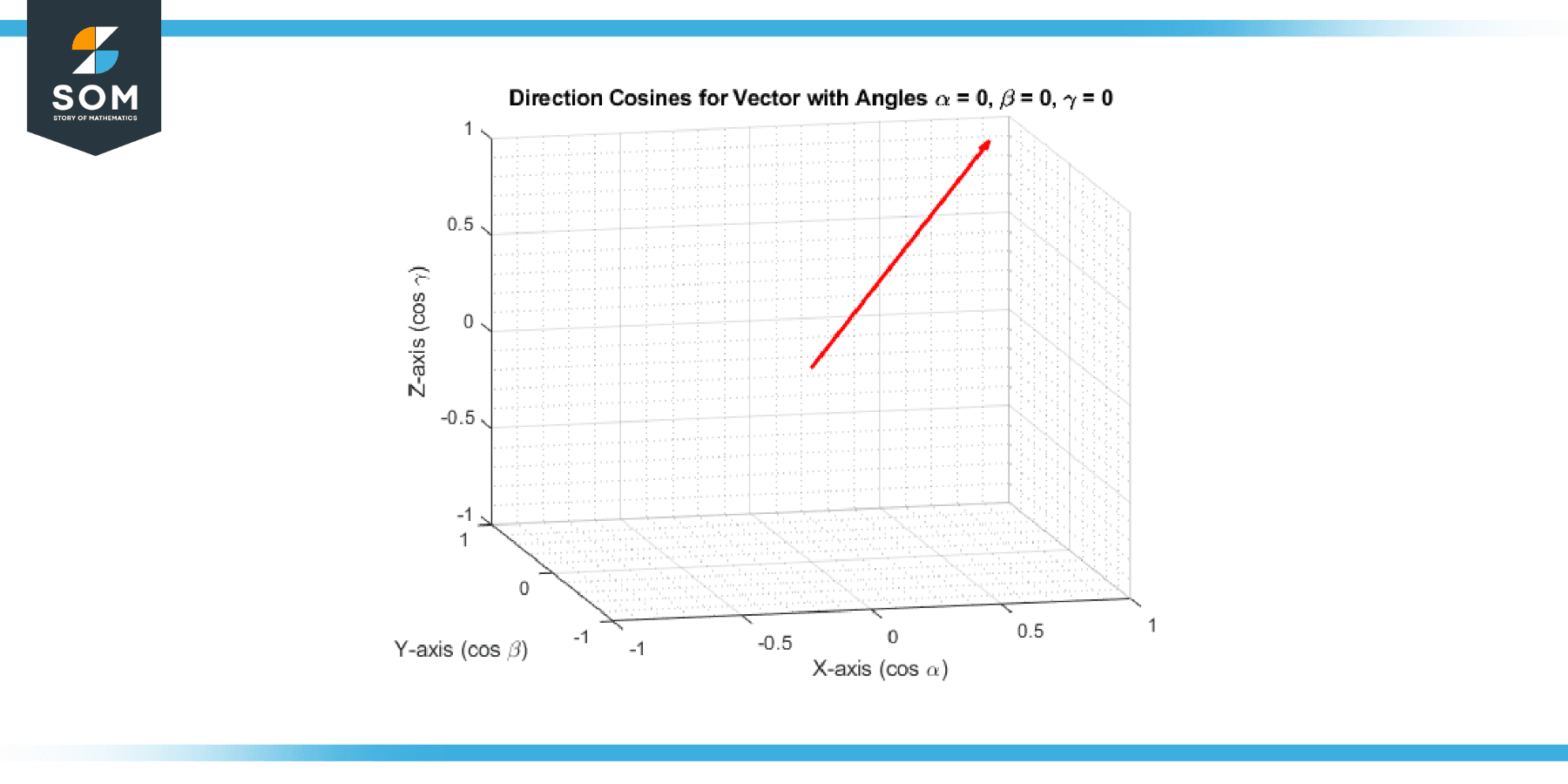
Figure-2.
Example 2
Determine the direction cosines for the vector having angles α = π/2, β = π/2, γ = π/2 with the coordinate axes.
Solution
The direction cosines are:
l = cos(π/2) = 0
m = cos(π/2) = 0
n = cos(π/2) = 0
Example 3
Determine the direction cosines for the vector having direction ratios of (1, 1, 1).
Solution
The magnitude of the vector is:
√(1² + 1² + 1²) = √(3)
Thus, the direction cosines are:
l = 1/√(3)
m = 1/√(3)
n = 1/√(3)
Example 4
Determine the direction cosines for the vector along the x-axis, having the angles with the coordinate axes are α = 0, β = π/2, γ = π/2.
Solution
Thus, the direction cosines are:
l = cos(0) = 1
m = cos(π/2) = 0
n = cos(π/2) = 0
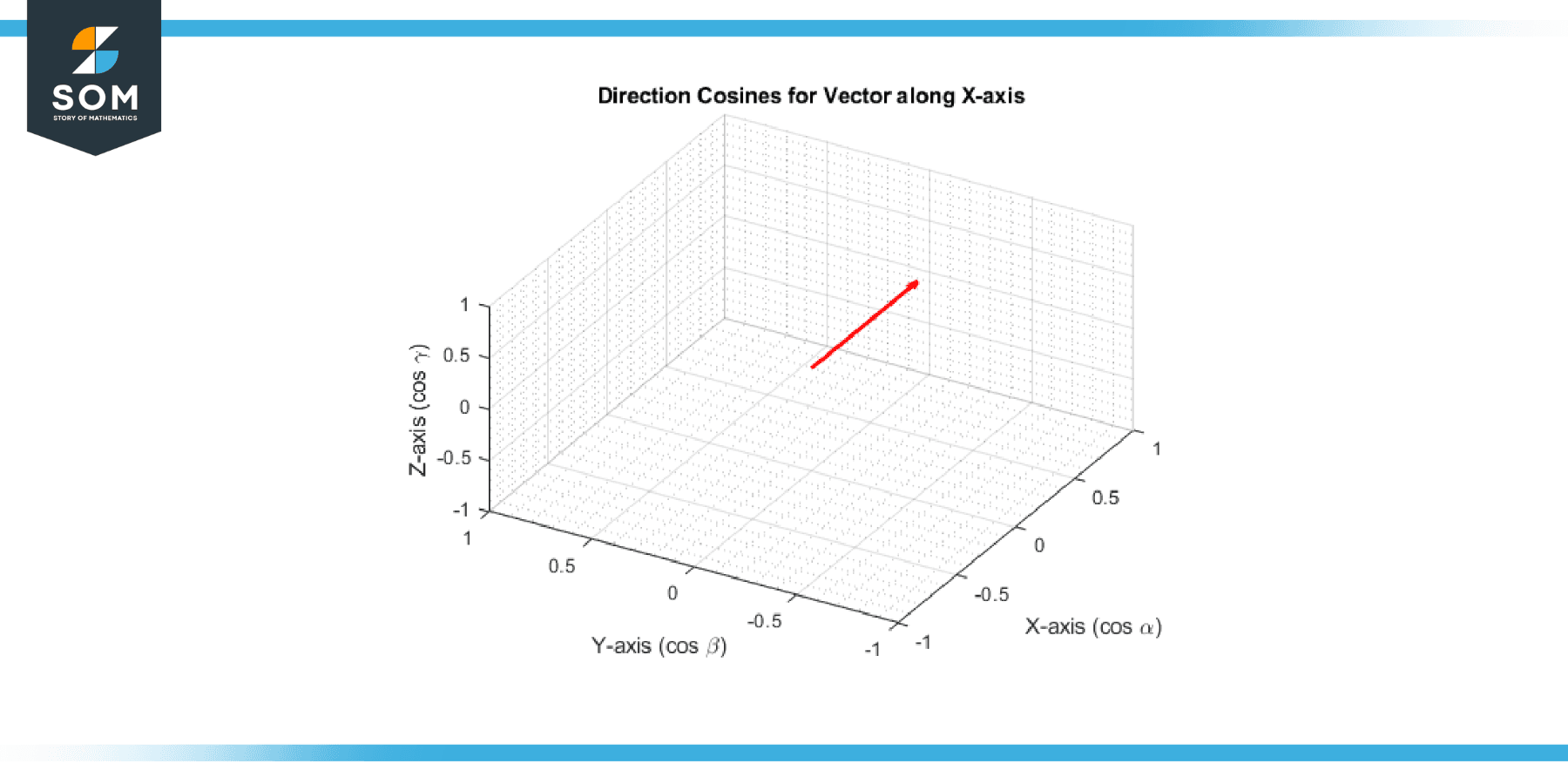
Figure-3.
Example 5
Determine the direction cosines for the vector along the y-axis, having the angles with the coordinate axes are α = π/2, β = 0, γ = π/2.
Solution
Thus, the direction cosines are:
l = cos(π/2) = 0
m = cos(0) = 1
n = cos(π/2) = 0
Example 6
Determine the direction cosines for the vector along the z-axis, having the angles with the coordinate axes are α = π/2, β = π/2, γ = 0.
Solution
Thus, the direction cosines are:
l = cos(π/2) = 0
m = cos(π/2) = 0
n = cos(0) = 1
Example 7
Determine the direction cosines for the vector having direction ratios of (-1, -1, -1),
Solution
The magnitude of the vector is:
√((-1)² + (-1)² + (-1)²) = √(3)
Thus, the direction cosines are:
l = -1/√(3)
m = -1/√(3)
n = -1/√(3)
Example 8
Determine the direction cosines for the vector having direction ratios of (1, -1, 0)
Solution
The magnitude of the vector is:
√((1)² + (-1)² + 0²) = √(2)
Thus, the direction cosines are:
l = 1/√(2)
m = -1/√(2)
n = 0
Applications
The concept of direction cosines is fundamental in various fields due to its utility in representing spatial relationships and transformations. Here are several applications:
Physics and Engineering
In fields such as mechanics, electrical engineering, and aerospace, understanding the direction and magnitude of forces and velocities is critical. Direction cosines are used in these fields to transform vectors between different coordinate systems, such as from Cartesian to spherical or cylindrical coordinates. For instance, in dynamics, they can help understand the orientation of a force vector in 3D space.
Computer Graphics and Robotics
Direction cosines form the basis of rotation matrices, extensively used in computer graphics for rotating and transforming objects. In robotics, they are used in kinematics to understand the orientation of robotic arms and joints in three dimensions.
Geography and Geology
Direction cosines can represent the orientation of geographical features, such as the slope and aspect of a hillside in physical geography or the dip and strike of a geologic layer in geology.
Crystallography
In crystallography, direction cosines describe the orientation of a crystal axis or plane about the standard crystallographic axes.
Astronomy
Astronomers use direction cosines to represent the position of celestial bodies on the celestial sphere relative to an observer’s local horizon.
Medicine
In medical imaging and surgical planning, understanding the spatial orientation of anatomical structures and medical devices is essential. These contexts often use direction cosines to represent and manipulate spatial orientations.
Navigation Systems
Direction cosines are extensively used in navigation systems, especially in aircraft and ship navigation. They assist in representing the vehicle’s orientation in 3D space, which is crucial for accurate navigation and control.
3D Game Development
In 3D game development and animation, direction cosines rotate and translate virtual objects within the game’s or animation’s 3D environment. It helps developers ensure that objects realistically interact with the virtual world.
Augmented Reality (AR) and Virtual Reality (VR)
In AR and VR technologies, direction cosines are a crucial tool for determining the orientation and viewpoint of the user in the virtual or augmented environment, enabling an immersive and interactive experience.
Biomechanics
In studying body movement, or biomechanics, direction cosines describe the orientation of bones and joints. This can be particularly useful in analyzing gait or other complex movements.
All images were created with MATLAB.
