JUMP TO TOPIC

This article explores the non adjacent angles, demystifying their properties, their relationships, and their roles in shaping the geometric world as we know it.
Defining Non Adjacent Angles
Non adjacent angles are two or more angles that do not share a common side (ray) or a common vertex (endpoint of the rays). They are distinct from each other and do not have any spatial relationship, like being next to each other or overlapping. Non adjacent angles are angles separated from each other in a geometric figure or context.
It’s worth noting that non adjacent angles can have different measures and do not need to be equal or related in any specific way.
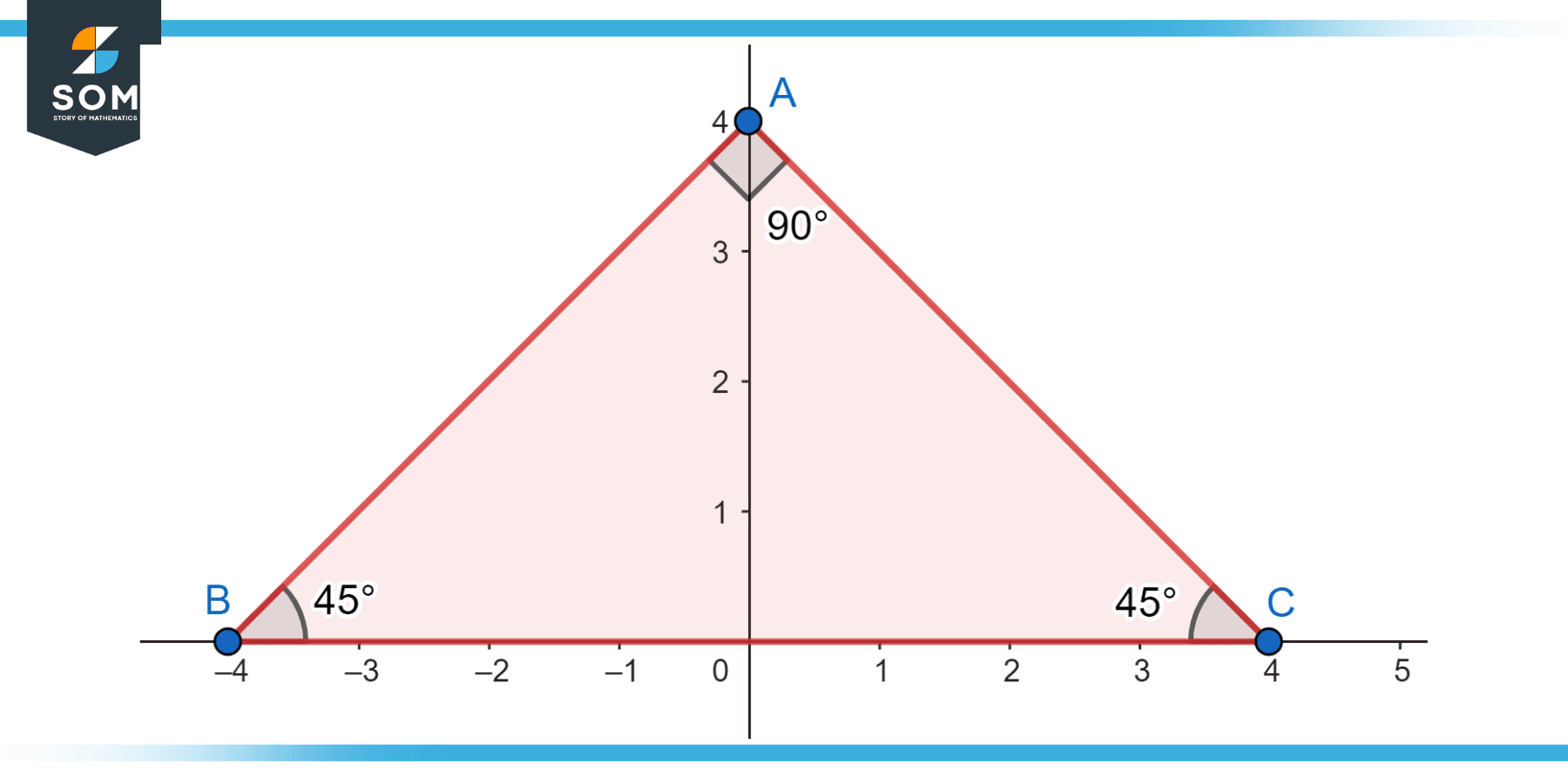
Figure-1.
Properties of Non Adjacent Angles
Non adjacent angles do not have a fixed set of properties like other specific types of angles, such as complementary or supplementary angles, mainly because their measurements are independent of each other. Here are a few characteristics that can be noted about non adjacent angles:
Lack of Shared Vertex or Side
Non-adjacent angles do not share a common vertex or a common side. Each angle is separate and does not touch the other angle.
Independent Measurements
The measurement of a non-adjacent angle is not related to another non-adjacent angle. They are independent of each other.
Various Locations
Non-adjacent angles can be located anywhere in the plane. They don’t have to be part of the same figure or diagram.
No Overlapping
Non-adjacent angles do not overlap each other.
Flexibility in Figures
In a given geometric figure, any angle that does not share a side or vertex with a certain angle can be considered non-adjacent to it. This allows great flexibility in working with these angles within different geometric contexts.
Exercise
Example 1
Consider a triangle ABC, and mention the non adjacent angles.
Solution
Angle ABC and angle BCA are adjacent because they share a common side and vertex. But, Angle ABC and angle CAB are non-adjacent because they do not share a common side.
Example 2
Consider the square ABCD, and mention the non adjacent angles.
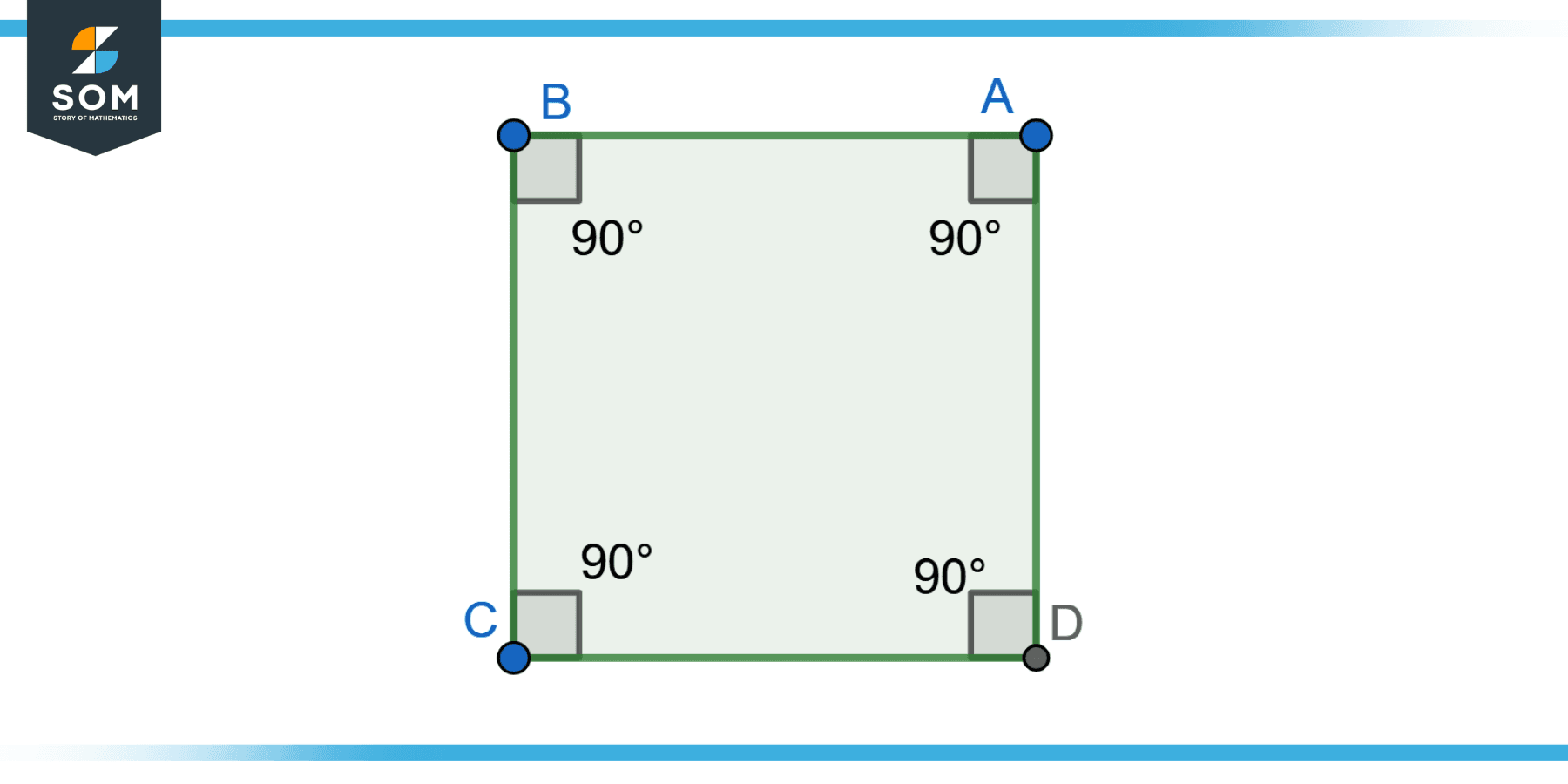
Figure-2.
Solution
In a square ABCD, the angles ∠BAD and ∠BCD are non-adjacent because they do not share a common side or vertex.
Example 3
Consider the pentagon ABCDE, and mention the non adjacent angles.
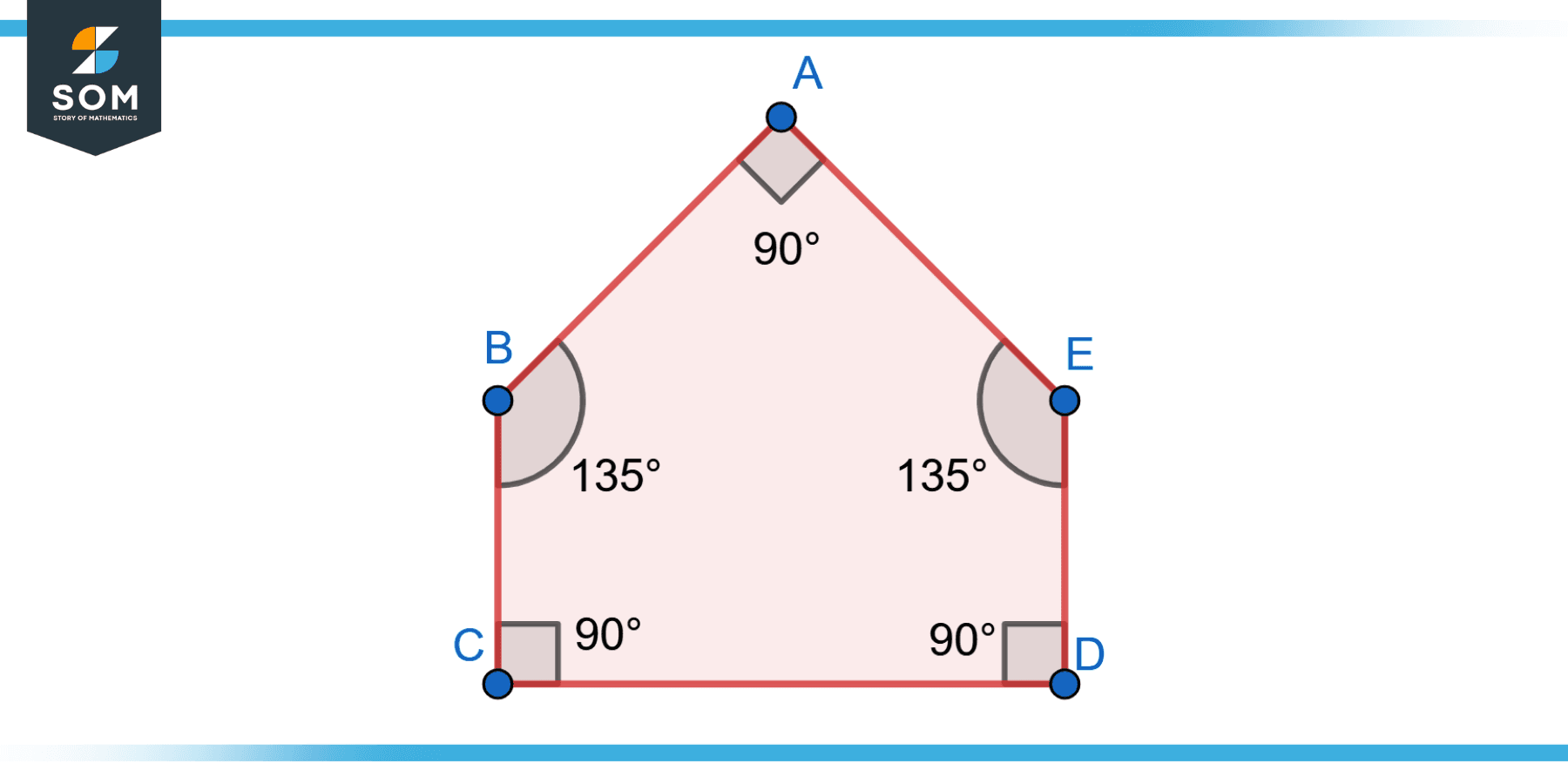
Figure-3.
Solution
In the Pentagon ABCDE, Angles ∠CAB and ∠BDE are non-adjacent angles because they do not share a common side or vertex.
Example 4
Consider the circle with diameter AB and mention the non adjacent angles.
Solution
In a circle with a diameter AB and any point C on the circumference, ∠ACB and ∠CAB are non-adjacent angles. They share a vertex but do not share a common side.
Example 5
Consider the triangles ABC and DEF, and mention the non adjacent angles.
Solution
Consider two separate triangles, ABC and DEF. Any angle from triangle ABC is non-adjacent to any angle from triangle DEF because they do not share a common side or a vertex.
Example 6
Consider the quadrilateral ABCD, and mention the non adjacent angles.
Solution
In an arbitrary quadrilateral ABCD, angles ∠DAB and ∠BCD are non-adjacent because they do not share a common side or vertex.
Example 7
Consider the Secant AB and find the non adjacent angles.
Solution
In a circle with a secant AB and a tangent at point B, the angle between the secant and the tangent and the angle subtended by the secant at the center of the circle are non-adjacent.
Applications
While non-adjacent angles themselves don’t directly find specific applications in various fields due to their lack of shared properties or relationship to each other, understanding these angles is fundamental to various applications of geometry in diverse fields.
Here are a few instances where the concept of non-adjacent angles (or, more broadly, the knowledge of angles) might play a role:
Architecture and Engineering
Non-adjacent angles can appear in the design and construction of buildings, bridges, or other structures. Identifying and working with these angles can be important in these structures’ design and stability analysis.
Computer Graphics and Game Design
When designing 3D models or game environments, understanding the concepts of angles, including non-adjacent angles, is crucial for creating realistic and visually pleasing graphics.
Physics
In fields such as optics or mechanics, understanding the relationship between angles can help in predicting the behavior of light or the motion of objects.
Geography and Cartography
When drawing or interpreting maps, the concept of angles, including non-adjacent angles, can play an essential role.
Astronomy
The angles between stars or other celestial bodies, often non-adjacent, can be important in celestial navigation or calculating astronomical distances.
Robotics
In robotics, angles are crucial in determining how a robot should move or react in a given environment. Non adjacent angles can be used to design robot navigation and path-planning algorithms.
Navigation and Aviation
Angles are essential for navigation, particularly in aviation and seafaring. Understanding non-adjacent angles can help plan flight or travel routes, interpret compass bearings, and more.
Interior Design
In the field of interior design, understanding angles can help create spaces that are aesthetically pleasing and functional. Non-adjacent angles can appear in furniture arrangements, room layouts, and more.
Cryptography
Some forms of cryptography, especially those based on geometric shapes or patterns, can use angles, including non-adjacent angles.
Historical Significance
Angles, including non-adjacent angles, have been foundational elements in geometry for thousands of years. While there isn’t a specific historical significance tied directly to non-adjacent angles, the evolution of geometric understanding, which includes the recognition of angles and their properties, has been integral to human history.
Ancient Civilizations
Ancient civilizations like the Egyptians and Babylonians had a keen understanding of basic geometric principles. They used this knowledge to build architectural wonders like the pyramids and to develop systems for land measurement, which required the identification and measurement of various types of angles, likely including non-adjacent ones.
Greek Geometry
The Greeks, most notably Euclid, formalized the study of geometry in works such as Euclid’s Elements. While Euclid didn’t explicitly talk about non-adjacent angles, his axioms and theorems laid the foundation for understanding geometric relationships, including the properties of angles.
Navigation and Exploration
The age of exploration from the 15th to 17th centuries heavily relied on understanding angles for celestial navigation. Mariners and explorers used the angles between stars or between a star and the horizon to find their way at sea. While these angles were not non-adjacent in the geometric sense, considering individual, separate angles was central to these navigational techniques.
Modern Geometry
In the modern era, understanding angles (including non-adjacent angles) is a foundational aspect of many branches of mathematics. It is deeply embedded in the study of shapes, sizes, and properties of spaces. This knowledge is crucial for many modern applications, including computer graphics, architecture, physics, engineering, etc.
All images were created with GeoGebra.
