JUMP TO TOPIC
The double angle theorem is the result of finding what happens when the sum identities of sine, cosine, and tangent are applied to find the expressions for $\sin (\theta + \theta)$, $\cos (\theta + \theta)$, and $\tan (\theta + \theta)$. The double angle theorem opens a wide range of applications involving trigonometric functions and identities.
The double angle theorem highlights the relationship shared between the sine, cosine, and tangent of the angle and twice the angle. This theorem becomes an essential tool in trigonometry – especially when evaluating and simplifying trigonometric expressions.
In this article, we’ll break down the important trigonometric identities that involve double angles. The discussion will also show how the identities were derived as well as how they can be applied to different word problems and applications.
What Is the Double Angle Theorem?
The double angle theorem is a theorem that states that the sine, cosine, and tangent of double angles can be rewritten in terms of the sine, cosine, and tangent of half these angles. From the name of the theorem, the double angle theorem allows one to work with trigonometric expressions and functions involving $2\theta$.
This leads to trigonometric identities showcasing the relationships between $\sin 2\theta$, $\cos 2\theta$, and $\tan 2\theta$.
| \begin{aligned}\boldsymbol{\sin 2\theta}\end{aligned} | \begin{aligned}\boldsymbol{\cos 2\theta}\end{aligned} | \begin{aligned}\boldsymbol{\tan 2\theta}\end{aligned} |
| \begin{aligned}\sin 2\theta &= 2\sin\theta \cos\theta\end{aligned} | \begin{aligned}\cos 2\theta &= \cos^2 \theta – som^2 \theta\\ &=2\cos^2 \theta -1\\&= 1-2\sin^2\theta \end{aligned} | \begin{aligned}\tan 2\theta &= \dfrac{2\tan\theta}{1 – \tan^2\theta}\end{aligned} |
Thanks to the double angle theorem and identities, it’s easier to evaluate trigonometric functions and identities involving double angles. The next section covers its application, so for now, let us show you the proof and all the components involving the double angle theorem.
Understanding the Double Angle Theorem
The double angle theorem focuses on finding a way to rewrite the trigonometric functions of $2\theta$ in terms of $\sin \theta$, $\cos \theta$, or $\tan \theta$. The identities for these may appear intimidating at first, but by understanding its components and proof, it will be much easier to apply them.
- Understanding $\boldsymbol{\sin 2 \theta = 2\sin\theta \cos\theta}$:
According to the double angle theorem for sine, the sine of double an angle is equal to twice the product of the sine and cosine of the angle.
\begin{aligned}\sin 60^{\circ} &= 2\sin 30^{\circ}\cos 30^{\circ}\\\sin \dfrac{\pi}{3} &= 2\sin \dfrac{\pi}{6} \sin \dfrac{\pi}{6}\end{aligned}
Now, to prove the double angle identity for sine, use the sum identity $\sin (A +B) = \sin A\cos B + \cos A\sin B$.
\begin{aligned}\sin 2\theta &= \sin (\theta + \theta)\\&= \sin \theta\cos \theta +\cos \theta\sin \theta\\&= 2\sin\theta \cos\theta \end{aligned}
- Understanding $\boldsymbol{\cos 2 \theta = \cos^2 \theta – \sin^2 \theta}$:
The double angle theorem for cosine states that the cosine of twice an angle is equal to the difference between the squares of the cosine and sine of the angle.
\begin{aligned}\cos 100^{\circ} &= \cos^2 50^{\circ} – \sin^2 50^{\circ}\\\cos \dfrac{\pi}{4} &= \cos^2 \dfrac{\pi}{8} – \sin^2 \dfrac{\pi}{8}\end{aligned}
To understand its origin, apply the sum identity for cosine: $\cos (A +B) = \cos A\cos B – \sin A\sin B$.
\begin{aligned}\cos 2\theta &= \cos (\theta + \theta)\\&= \cos \theta\cos \theta -\sin\theta\sin \theta\\&= \cos^2\theta – \sin^2\theta \end{aligned}
The double angle identities for cosine can also be rewritten in two other forms. To derive the two remaining identities for $\cos 2\theta$, apply the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$.
| \begin{aligned}\boldsymbol{\cos 2\theta} &= \boldsymbol{2\cos^2\theta – 1}\end{aligned} | \begin{aligned}\boldsymbol{\cos 2\theta} &= \boldsymbol{1- 2\sin^2\theta}\end{aligned} |
| \begin{aligned}\cos 2\theta &= \cos^2\theta – \sin^2\theta\\&= \cos^2\theta – (1- \cos^2\theta)\\&= 2\cos^2\theta – 1\end{aligned} | \begin{aligned}\cos 2\theta &= \cos^2\theta – \sin^2\theta\\&= (1 -\sin^2 \theta) – \sin^2\theta\\&= 1 – 2\sin^2\theta\end{aligned} |
- Understanding $\boldsymbol{\tan 2 \theta = \dfrac{2\tan\theta}{1 – \tan^2 \theta}}$:
The tangent of double the angle is equal to the ratio of the following: twice the tangent of the angle and the difference between $1$ and the square of the angle’s tangent.
\begin{aligned}\tan 90^{\circ} &= \dfrac{2 \tan 45^{\circ}}{1 -\tan^2 45^{\circ}}\\\tan \dfrac{\pi}{2} &= \dfrac{2 \tan \dfrac{\pi}{4}}{1 – \tan^2 \dfrac{\pi}{4}}\end{aligned}
To prove the double angle formula for tangent, apply the sum identity for tangent: $\tan (A + B) = \dfrac{\tan A + \tan B}{1 – \tan A\tan B}$.
\begin{aligned}\tan 2\theta &= \tan (\theta + \theta)]\\&= \dfrac{2 \tan \theta}{1 – \tan\theta \tan\theta}\\&= \dfrac{2\tan \theta}{1 – \tan^2\theta}\end{aligned}
Now that we’ve shown the double angle theorem’s components and proof, it’s time to learn when it is best to apply the double angle theorem and the process of using the three identities.
How To Use the Double Angle Theorem?
To use the double angle theorem, identify the trigonometric formula that best applies to the problem. Find the value of $\theta$ given $2\theta$ then apply appropriate algebraic and trigonometric techniques to simplify a given expression.
Here are some instances when the double angle theorem comes in handy the most:
- Simplifying and evaluating trigonometric expression where it’s easier to work with the sine, cosine, or tangent of $\theta$ instead of $2\theta$
- When exact values of $\sin \theta$, $\cos \theta$, or $\tan \theta$ are given and what’s required is either $\sin 2\theta$, $\cos 2\theta$, or $\tan \theta$
- Deriving and proving other trigonometric identities that involve double-angle identities
In the problems that follow, we’ll show you different examples and ways to utilize the double angle theorem. We begin by seeing how we can apply the double angle theorem to simplify and evaluate trigonometric expressions.
Example 1
Suppose that $\cos \theta = -\dfrac{12}{13}$ and the angle $\theta$ lies in the third quadrant. Find the exact values of the following trigonometric expressions:
a. $\sin 2\theta$
b. $\cos 2\theta$
c. $\tan 2\theta$
Solution
When given problems like this, the first step is to construct a triangle as a guide in finding the position and values of $\theta$. Find the missing side by applying the Pythagorean theorem, which is $a^2 + b^2 = c^2$.
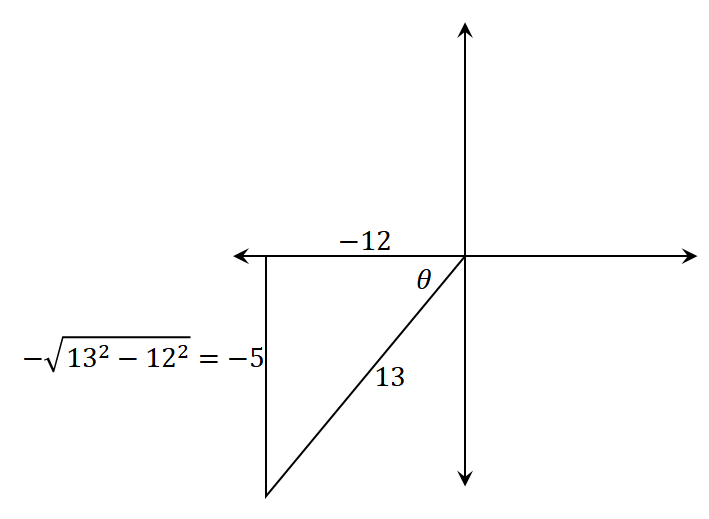
Now, identify the appropriate double angle theorem to apply before rewriting the expression. Since we’re looking for $\sin 2\theta$, apply the double-angle identity $\sin 2\theta = 2 \sin\theta \cos\theta$. Sine reflects the ratio between the side opposite the angle and the hypotenuse and is negative in the third quadrant, so $\sin \theta = -\dfrac{5}{13}$.
\begin{aligned}\sin 2\theta &= 2\sin \theta \cos \theta\\&= 2\left(-\dfrac{5}{13}\right) \left(-\dfrac{12}{13}\right)\\&= \dfrac{120}{169}\end{aligned}
a. This means that $\sin 2\theta$ is equal to $\dfrac{120}{169}$.
To find the exact value of $\cos 2\theta$, apply the double angle theorem $\cos 2\theta = \cos^2 \theta – \sin^2 \theta$. We already know the exact values for cosine and sine, so use them to evaluate the expression for $\cos 2\theta$.
\begin{aligned}\cos 2\theta &= \cos^2\theta – \sin^2\theta\\&= \left(-\dfrac{12}{13}\right)^2 -\left(-\dfrac{5}{13}\right)^2\\&= \dfrac{119}{169}\end{aligned}
b. Hence, we have $\cos 2\theta = \dfrac{119}{169}$.
Similarly, let’s use the double angle theorem for tangent $\tan 2\theta = \dfrac{2\tan \theta}{1 – \tan^2\theta}$. Using the same graph and knowing that tangent is positive in the third quadrant, $\tan \theta = \dfrac{5}{12}$.
\begin{aligned}\tan 2\theta &= \dfrac{2\tan \theta}{1 – \tan^2\theta}\\&= \dfrac{2 \cdot \dfrac{5}{12}}{1 – \left(\dfrac{5}{12}\right)^2}\\&= \dfrac{120}{119}\end{aligned}
c. This shows that $\tan 2\theta$ is equal to $\dfrac{120}{119}$.
It’s also easier to simplify trigonometric expressions all thanks to the double angle theorem. To rewrite a trigonometric expression using the double angle theorem, double-check which of the three identities apply by inspecting the expression.
We’ve prepared more examples highlighting the importance of double angle theorems in problems like the ones shown below.
Example 2
What is the simplified form of $12\sin(12x)\cos(12x)$?
Solution
First, determine which of the double angle identities apply. If we let the angle $\theta$ represent $12x$, we have:
\begin{aligned}\theta &= 12x \\12\sin (12x)\cos(12x) &= 12 \sin\theta \cos\theta \\&= 6(2\sin\theta \cos\theta)\end{aligned}
Does the expression $2\sin\theta \cos\theta$ look familiar? It’s the equivalent of $\sin 2\theta$ as we have established in the earlier section. Rewrite our expression using the double angle theorem as shown below.
\begin{aligned}6(2\sin\theta \cos\theta) &= 6 \sin 2\theta \\&= 6 \sin (2 \cdot 12x)\\&= 6\sin (24x)\end{aligned}
This means that through the double angle theorem, $12\sin(12x)\cos(12x)$ is equivalent to $6\sin (24x)$.
Example 3
Using the double angle theorem, show that $1 – \sin (2\theta)$ is equivalent to $(\sin \theta – \cos \theta)^2$.
Solution
Whenever a trigonometric expression or identity contains $2\theta$, check whether one of the three double angle identities can be used to simplify the expression.
This means that if we want to prove that $1 – \sin (2\theta) = (\sin \theta – \cos \theta)^2$ is true, we want the right-hand side of the equation to be equivalent to $1 – 2\sin\theta\cos\theta$.
- Apply the perfect square trinomial property $(a – b)^2 = a^2 -2ab + b^2$ to expand the left-hand side.
- Group $\sin^2\theta$ and $\cos^2\theta$ together.
- Use the Pythagorean identity $\sin^2\theta + \cos^2 \theta = 1$ to simplify the expression.
\begin{aligned}1 – \sin(2\theta)&= (\sin \theta – \cos\theta)^2\\&= \sin^2\theta- 2\sin\theta \cos\theta + \cos^2\theta\\&= (\sin^2\theta + \cos^2\theta) – 2\sin\theta\cos\theta\\&= 1- 2\sin\theta \cos\theta\\&= 1- 2\sin\theta \cos\theta\\&= 1- \sin(2\theta) \end{aligned}
This confirms that $1 – \sin (2\theta)$ is equivalent to $(\sin \theta – \cos \theta)^2$.
Practice Question
1. Suppose that $\sin \theta = \dfrac{21}{29}$ and the angle $\theta$ lies in the second quadrant. What is the exact value of $\sin 2\theta$?
A. $-\dfrac{840}{841}$
B. $-\dfrac{420}{841}$
C. $\dfrac{420}{841}$
D. $\dfrac{840}{841}$
2. Suppose that $\tan \theta = -\dfrac{7}{24}$ and the angle $\theta$ lies in the fourth quadrant. What is the exact value of $\cos 2\theta$?
A. $-\dfrac{527}{625}$
B. $-\dfrac{98}{625}$
C. $\dfrac{98}{625}$
D. $\dfrac{527}{625}$
3. Which of the following shows the simplified form of $1 – 2\sin^2 36^{\circ}$?
A. $\sin 18^{\circ}$
B. $\cos 18^{\circ}$
C. $2\cos 18^{\circ}$
D. $\sin 36^{\circ}$
4. Which of the following shows the simplified form of $6 \sin(4y)\cos(4y)$?
A. $3 \sin(2y)\cos(2y)$
B. $3 \sin (8y)$
C. $6\cos (8y)$
D. $6 \sin (8y)$
5. Which of the following trigonometric expressions is equivalent to $(\sin \theta + \cos \theta)^2$?
A. $1 – \cos 2\theta$
B. $1 +\cos 2\theta$
C. $1 – \sin 2\theta$
D. $1 + \sin 2\theta$
6. Which of the following trigonometric expressions is equivalent to $3\sin\theta \cos^2\theta – \sin^3 \theta$?
A. $3\cos \theta$
B. $3\sin \theta$
C. $\sin (3\theta)$
D. $\cos (3\theta)$
Answer Key
1. A
2. D
3. B
4. B
5. D
6. C< /div>
