JUMP TO TOPIC
The side splitter theorem establishes the relationship between the line segments formed by splitting the two sides of a triangle through another line segment. When the line segment is parallel with the third side, the line segments are proportional to each other.
This article covers all the fundamentals needed to understand the side splitter theorem. By the end of this discussion, we want readers to feel confident when applying the side splitter theorem to solve problems that involve similar triangles and their line segments.
What Is the Side Splitter Theorem?
The side splitter theorem is a theorem that states that when a line passes through the two sides of a triangle and is parallel to the third remaining side, the line divides the two sides proportionally.
Take a look at the triangle $\Delta ABC$ for example, the line $\overline{DE}$ goes through the two sides of the triangle $\overline{AB}$ and $\overline{AC}$. It is also parallel to the third side, $\overline{BC}$.
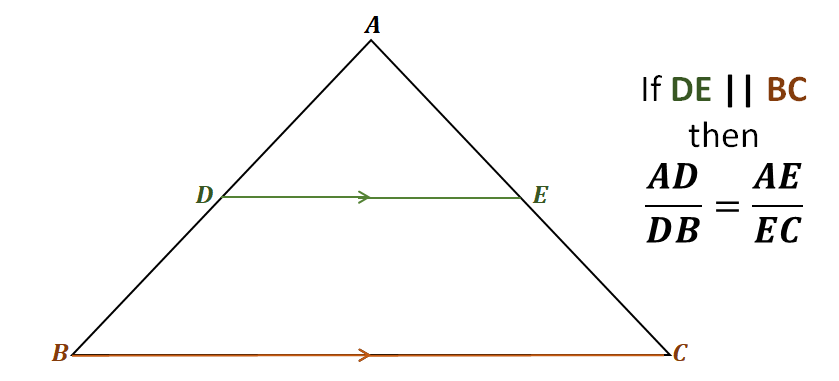
This means that through the side splitter theorem, the following line segments are proportional to each other: $\overline{AD}$ and $\overline{DB}$, as well as $\overline{AE}$ and $\overline{EC}$. The ratios of each of these pairs of line segments are equal.
\begin{aligned}\color{DarkBlue}\textbf{Side Spli} &\color{DarkBlue}\textbf{tter Theorem}\\\\\text{Given that } {\color{DarkGreen}\boldsymbol{\overline{DE}}} &\parallel {\color{DarkOrange}\boldsymbol{\overline{BC}}}, \text{ we have}:\\\\\boldsymbol{\dfrac{AD}{DB}} &=\boldsymbol{\dfrac{AE}{EC}} \end{aligned}
Review the conditions for the side splitter theorem and try to confirm whether the triangle that is shown below satisfies the rule for proportionality.
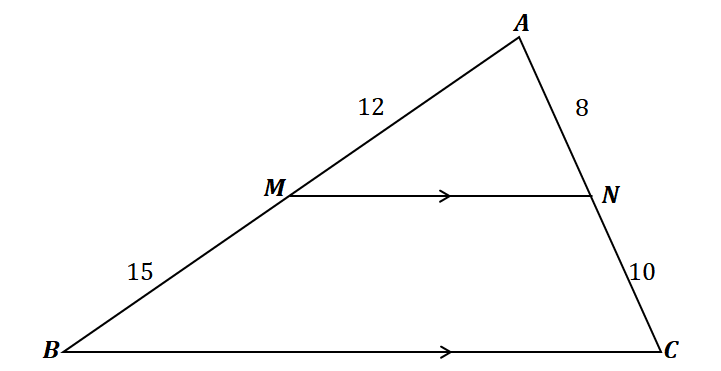
To understand the side splitter theorem, take a look at the triangle shown above.
As can be seen, $\overline{MN}$ passes through the two sides of $\Delta ABC$: $\overline{AB}$ and $\overline{AC}$. In addition, $\overline{MN}$ is parallel with the third side, $\overline{BC}$. This means that the line segments should be proportional as per the side splitter theorem.
\begin{aligned}\dfrac{\overline{AM}}{\overline{MB}} &= \dfrac{\overline{AN}}{\overline{NC}}\\\dfrac{12}{15} &= \dfrac{8}{10}\\\dfrac{4}{5}&\overset{\checkmark}{=} \dfrac{4}{5}\end{aligned}
Now that we’ve highlighted how the side splitter theorem works, let’s work on its proof to have a better understanding of the theorem.
How To Prove the Side Splitter Theorem
To prove the side splitter theorem, apply the properties of line segment addition and triangle similarity. First, construct a triangle where a line segment passes through the two sides of the triangle as shown below. Make sure that the third side is parallel with the remaining side of the triangle.
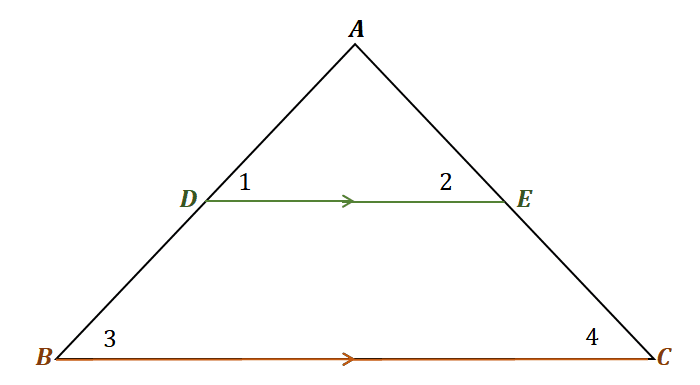
The triangle shown above satisfies the conditions we’ve mentioned. Since $\overline{DE} \parallel \overline{BC}$, the angles $\angle 1$ and $\angle 3$ are corresponding angles. Similarly, $\angle 2$ and $\angle 4$ are corresponding equals. Recall that in parallel lines, corresponding angles are equal.
Hence, we have the following:
\begin{aligned}\angle 1&= \angle 3\\\angle 2 &= \angle 4\end{aligned}
When two of the triangle’s angles are equal to the second triangle’s angles, by the Angle-Angle similarity, $\Delta ADE$ and $\Delta ABC$ are similar triangles. This means that the lengths of the two triangles are also proportional to each other.
\begin{aligned}\dfrac{\overline{AD}}{\overline{AB}} &= \dfrac{\overline{AE}}{\overline{AC}}\end{aligned}
Write the two sides of the triangle as a sum of the shorter line segments. Rewrite the proportion shown above to observe the relationship shared between the line segments.
\begin{aligned}\overline{AB} &= \overline{AD}+\overline{DB}\\\overline{AC}&=\overline{AE}+\overline{EC}\\&\downarrow\\\dfrac{\overline{AD}}{\overline{AB}}&= \dfrac{\overline{AE}}{\overline{AC}}\\\dfrac{\overline{AD}}{\overline{AD}+\overline{DB}}&= \dfrac{\overline{AE}}{\overline{AE}+\overline{EC}}\end{aligned}
Apply appropriate algebraic properties to show that the side splitter theorem is true.
\begin{aligned}\overline{AD}\cdot\overline{AE}+\overline{AD}\cdot\overline{EC}&= \overline{AE}\cdot\overline{AD}+\overline{AE}\cdot\overline{DB}\\\overline{AD}\cdot\overline{EC}&= \overline{AE}\cdot\overline{DB}\\\dfrac{\overline{AD}}{\overline{DB}}&= \dfrac{\overline{AE}}{\overline{EC}}\end{aligned}
This confirms that the line segments split by the new internal line segment are proportional. Now, it’s time to understand how to apply this theorem to solve different problems.
How To Use the Side Splitter Theorem
To use the side splitter theorem when finding unknown lengths in a given triangle, check whether the line segment satisfies the condition for the side splitter theorem first. If they do, use the fact that the line segments split by the line are proportional to each other.
Here’s a guide when applying the side splitter theorem to solve problems:
1. Determine whether the line segment passing through the sides of the triangle is parallel with the third side.
2. If it does, identify the lengths of the new line segments resulting from the split of the triangle’s two sides.
3. Equate their ratios to find the unknown lengths or values.
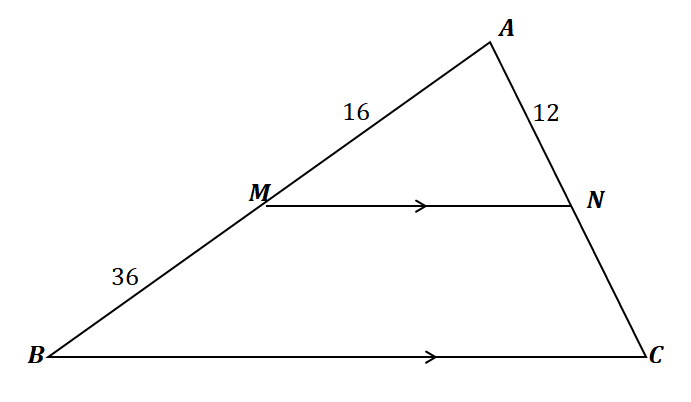
Let’s apply what we’ve learned to find the length of $\overline{NC}$. First, let’s confirm that we can use the side splitter theorem for this problem.
\begin{aligned}\overline{MN} \text{ splits } &\overline{AB} \,\,\&\,\, \overline{AC}\\\overline{MN} &\parallel \overline{BC}\end{aligned}
Hence, the side-splitter theorem applies to the triangle shown above. Now, relate the line segments $\overline{AM}$ and $\overline{MB}$ as well as $\overline{AN}$ and $\overline{NC}$ by equating their ratios. Solve for $\overline{NC}$ by cross-multiplying the ratios and simplifying the equation.
\begin{aligned}\dfrac{\overline{AM}}{\overline{MB}} &= \dfrac{\overline{AN}}{\overline{NC}}\\\dfrac{16}{36} &= \dfrac{12}{\overline{NC}}\\16\overline{NC} &= 12(36)\\\overline{NC}&=\dfrac{12(36)}{16}\\&= 27\end{aligned}
Hence, $\overline{NC}$ has a length of $27$ units. This shows that through the side splitter theorem, it’s now possible to work on more problems involving triangles and their line segments. Try out the problems in the next section to master this topic!
Example 1
Using the triangle shown below and given that $\overline{MN} \parallel \overline{BC}$, what is the value of $x$?
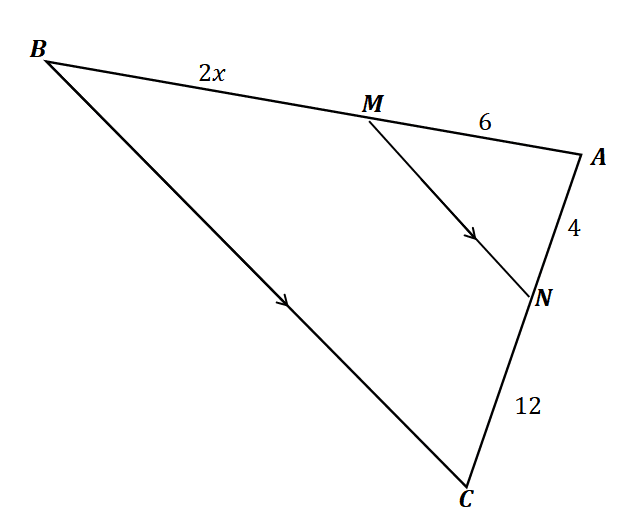
Solution
The line segment $\overline{MN}$ splits the two sides of the triangle $\angle ABC$: $\overline{AM}$ and $\overline{MB}$ as well as $\overline{AN}$ and $\overline{NC}$. In addition, $\overline{MN}$ is parallel to $\overline{BC}$, so using the side splitter theorem, we have the following:
\begin{aligned}\dfrac{\overline{AM}}{\overline{MB}} &= \dfrac{\overline{AN}}{\overline{NC}}\end{aligned}
Substitute the values and expression for the line segments then solve for $x$.
\begin{aligned}\dfrac{6}{2x} &= \dfrac{4}{12}\\6(12)&= 4(2x)\\72 &= 8x\\x&= 9\end{aligned}
This means that by using the side splitter theorem, we now know that $x = 9$.
Example 2
Using the triangle shown below and given that $\overline{MN} \parallel \overline{BC}$, what is the value of $x$?
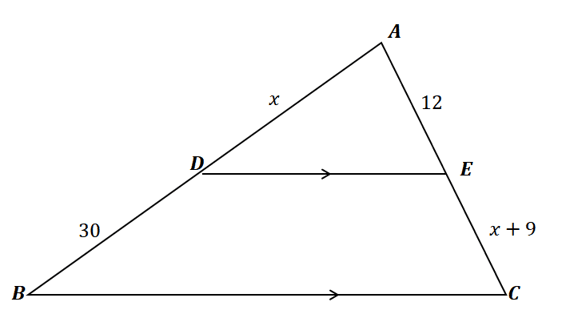
Solution
Similar to the previous problem, since $\overline{DE}$ splits the sides of $\Delta ABC$ and it is parallel to $\overline{BC}$, the split line segments are proportional to each other. This means that the ratios $\overline{AD} : \overline{DB}$ and $\overline{AE} : \overline{EC}$ are equal.
\begin{aligned}\dfrac{\overline{AD}}{\overline{DB}} &= \dfrac{\overline{AE}}{\overline{EC}}\end{aligned}
Use the given values and expressions for these line segments. Apply algebraic techniques learned in the past to solve the resulting equation.
\begin{aligned}\dfrac{x}{30} &= \dfrac{12}{x + 9}\\x(x + 9) &= 12(30)\\x^2 + 9x &= 360\\x^2 + 9x – 360&=0\\ (x – 24)(x + 15)&= 0\\x = 24\,&,\,x =-15\end{aligned}
Since $x$ represents the measure of $\overline{AD}$, it can never be negative. Hence, $x = 24$.
Example 3
Sheldon plans to create a triangular fence to protect his lake property from wild animals. He sketched a guide for the number of materials for his fence as shown below. He intends to construct a tiny bridge at the center of the lake and parallel to the third side of the fenced lot. What is the length of $\overline{AC}$?
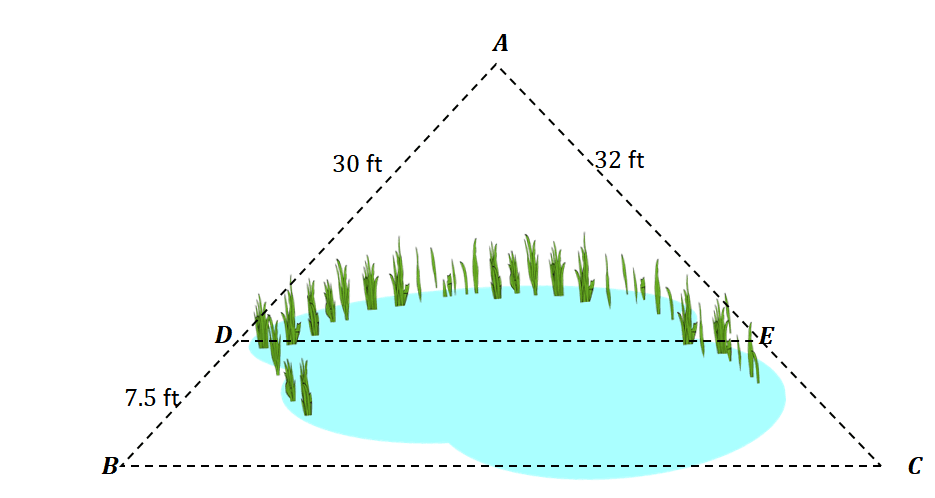
Solution
The triangle shown above shows split sides forming the following line segments: $\overline{AD}$, $\overline{DB}$, $\overline{AE}$, and $\overline{EC}$. Using the side splitter theorem, we have the equation shown below.
\begin{aligned}\dfrac{\overline{AD}}{\overline{DB}}&= \dfrac{\overline{AE}}{\overline{EC}} \\\dfrac{30}{7.5} &= \dfrac{32}{\overline{EC}}\\30 \cdot \overline{EC} &= 32(7.5)\\\overline{EC} &= \dfrac{32(7.5)}{30}\\&= 8\end{aligned}
To find the length of $\overline{AC}$, add the measures of the line segments $\overline{AE}$ and $\overline{EC}$.
\begin{aligned}\overline{AC} &= \overline{AE}+ \overline{EC}\\&=32 + 8\\&= 40\end{aligned}
Hence, the length of $\overline{AC}$ is $40$ units long.
Practice Question
1. Using the triangle shown below and given that $\overline{MN} \parallel \overline{BC}$, which of the following shows the value of $y$?
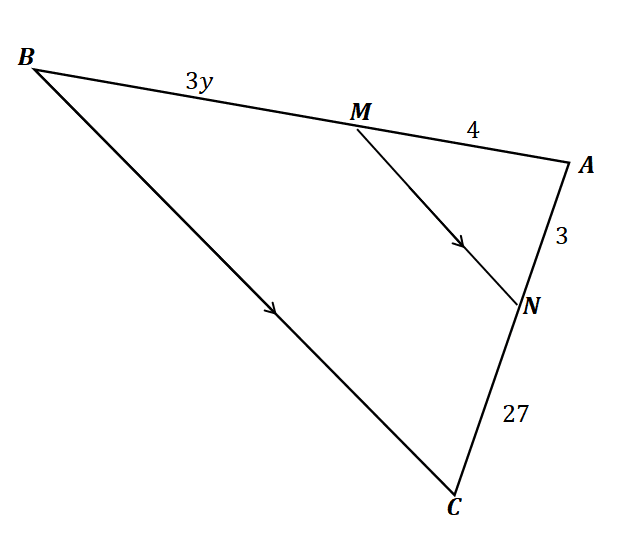
A. $y = 6$
B. $y = 9$
C. $y = 10$
D. $y = 12$
2. Using the triangle shown below and given that $\overline{DE} \parallel \overline{BC}$, which of the following shows the value of $y$?
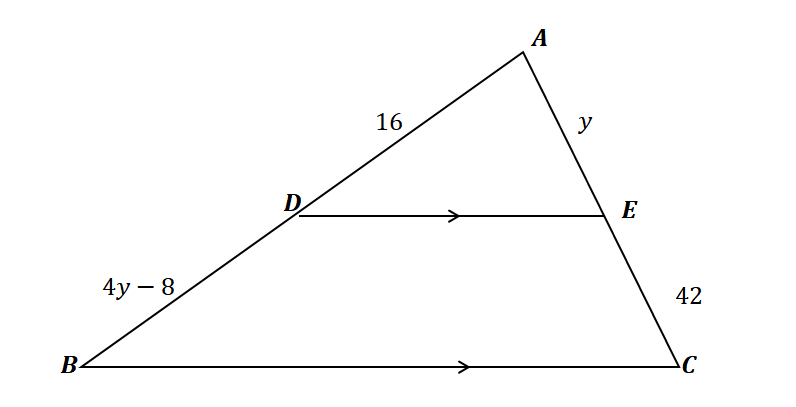
A. $y= 10$
B. $y = 12$
C. $y = 14$
D. $y = 16$
3. Using the triangle shown below and given that $\overline{MN} \parallel \overline{BC}$, which of the following shows the value of $x$?
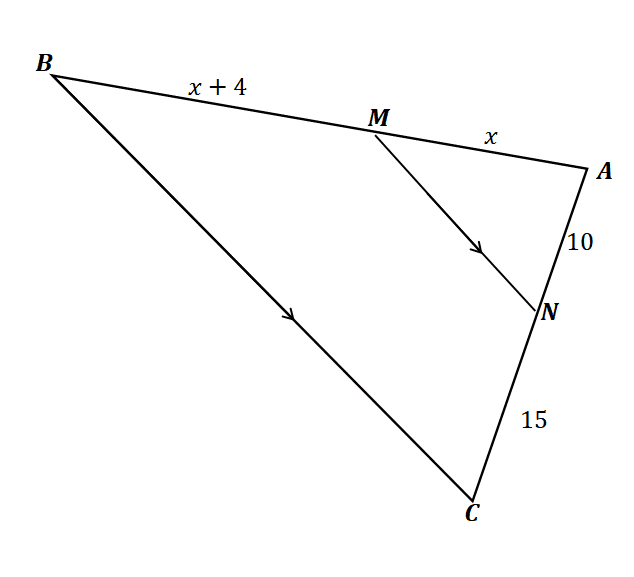
A. $x = 18$
B. $x= 20$
C. $x = 21$
D. $x = 24$
4. Using the triangle shown below and given that $\overline{DE} \parallel \overline{BC}$, which of the following shows the value of $x$?
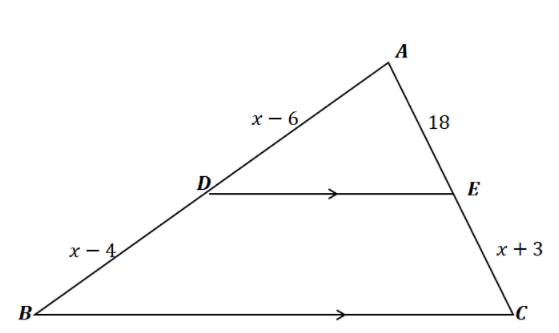
Answer Key
1. D
2. C
3. C
4. A
