Equation vs Expression – Definition, Applications, and Examples

What Is the Difference Between Equation vs Expression

The main difference between an expression and an equation is that an expression represents a mathematical “phrase” comprising numbers, variables, and operations without an equal sign, while an equation is a mathematical “sentence” asserting the equality of two expressions, always including an equal sign.

Both “equation” and “expression” are fundamental terms in mathematics, and while they might sound similar, they refer to different concepts. Here’s a breakdown of their differences:

Expression

An expression is a combination of numbers, variables, and operations. For example, 5 * x + 3 or 2 *$x^2$ – 7 * y + 10. An expression does not have an equals sign (=). It doesn’t necessarily represent a complete thought in mathematical terms. Think of it as a phrase in the language of mathematics. Expressions have value. For instance, if you plug in a value for x in the expression 5 * x + 3, you can evaluate the expression to get a single number.

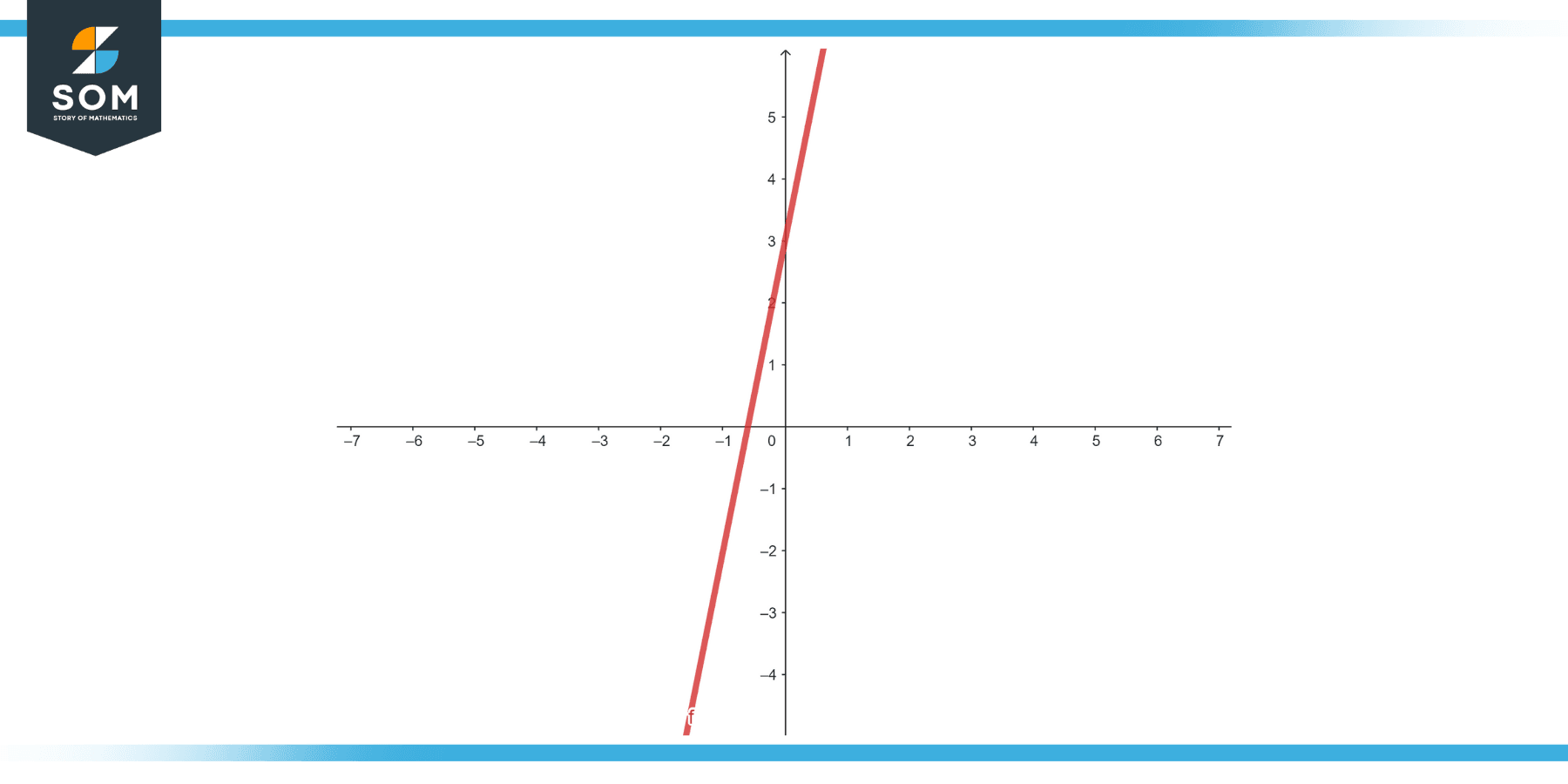
Figure-1.

Equation

An equation states that two expressions are equal, meaning they have the same value. For example, 2 + 3 = 5 or 5x + 3 = 23. An equation always includes an equals sign (=). It represents a complete thought, stating that two things are equal. Using the language analogy, it’s a complete sentence. Equations can be true or false. For example, the equation 3 + 2 = 6 is false, while the equation 3 + 2 = 5 is true. In summary, while both expressions and equations deal with numbers, variables, and operations, expressions are mathematical “phrases” that can be evaluated to give a value, whereas equations are mathematical “sentences” that state the equality between two expressions.

Properties

Both equations and expressions have properties that derive from the foundational principles of algebra. Let’s delve into these properties:

Expression Properties

Commutative Property (of Addition and Multiplication)

For any numbers a and b, the order in which you add or multiply them doesn’t change the result. a + b = b + a a × b = b × a

Associative Property (of Addition and Multiplication)

For any numbers a, b, and c, the way in which you group them when adding or multiplying doesn’t change the result. (a + b) + c = a + (b + c) (a × b) × c = a × (b × c)

Distributive Property

Multiplication distributes over addition. a × (b + c) = a × b + a × c

Identity Property

For addition, the identity is 0 because any number plus 0 is the number itself. For multiplication, the identity is 1 because any number times 1 is the number itself. a + 0 = a a × 1 = a

Inverse Property

For every number, there’s an additive inverse so that their sum is zero. Similarly, for every non-zero number, there’s a multiplicative inverse so that their product is one. a + (-a) = 0 a × (1/a) = 1 for a ≠ 0

Equation Properties

Reflexive Property

Any quantity is equal to itself. a = a

Symmetric Property

If one quantity equals another, then the second is equal to the first. If a = b, then b = a

Transitive Property

If one quantity equals a second, and the second equals a third, then the first quantity equals the third. If a = b and b = c, then a = c

Substitution Property

If two quantities are equal, one can be substituted for the other in any equation or expression. If a = b, then a can replace b in any expression or equation.

Addition and Multiplication Properties of Equality

If you add or multiply each side of an equation by the same number, the two sides remain equal. If a = b, then a + c = b + c If a = b, then a × c = b × c

Division Property of Equality

If you divide each side of an equation by the same non-zero number, the two sides remain equal. If a = b and c ≠ 0, then a/c = b/c Remember that while properties of expressions are related to manipulating and simplifying them, properties of equations relate to maintaining equality and deducing relationships between quantities.

Exercise 

Example 1

Expression: $4x+7$

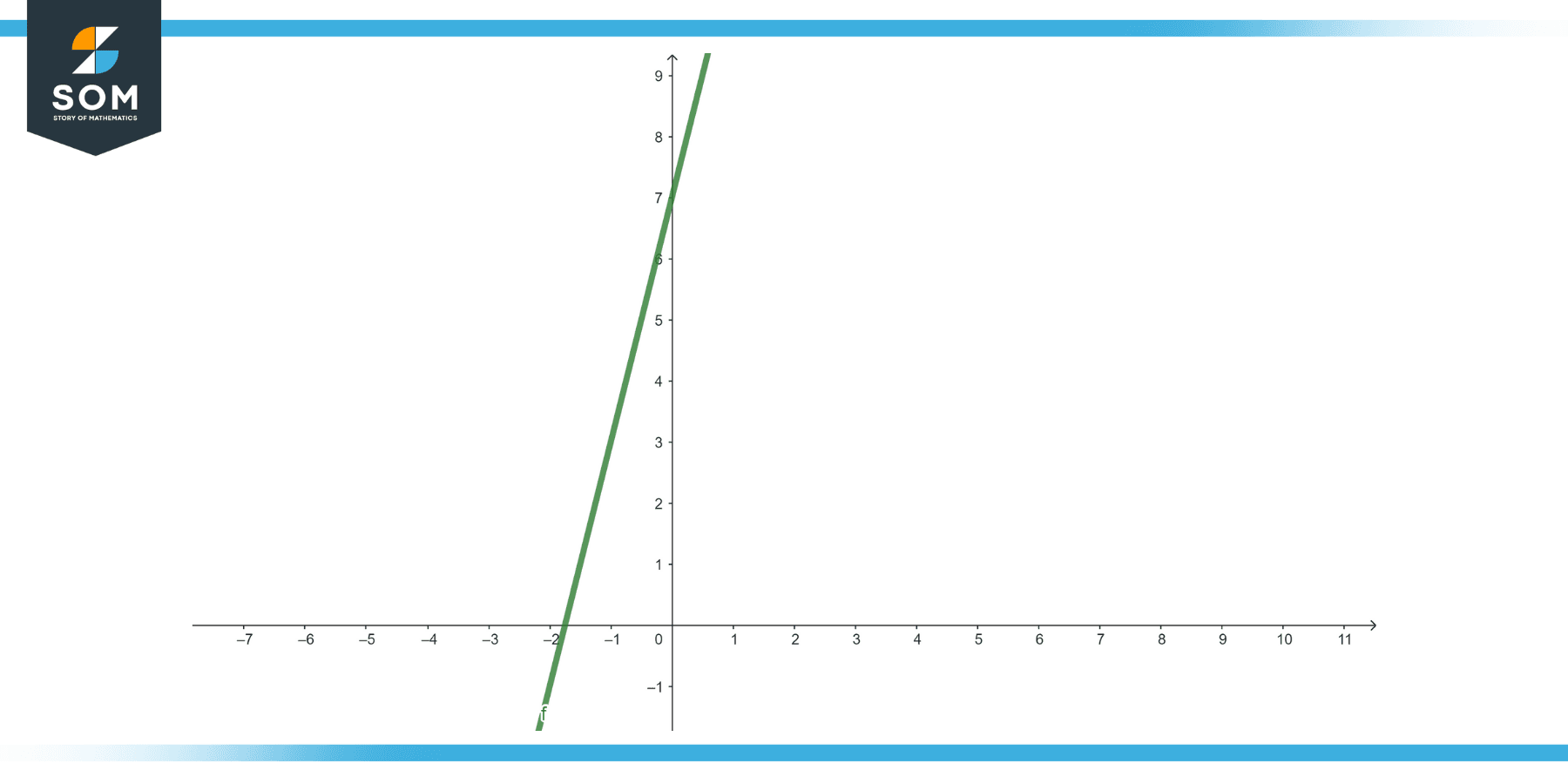
Figure-2.

Solution

This is a simple algebraic expression in terms of $x$. Without a specific value for $x$, we cannot evaluate it further.

Example 2

Expression: 3$(y^2)$ − 5y + 8

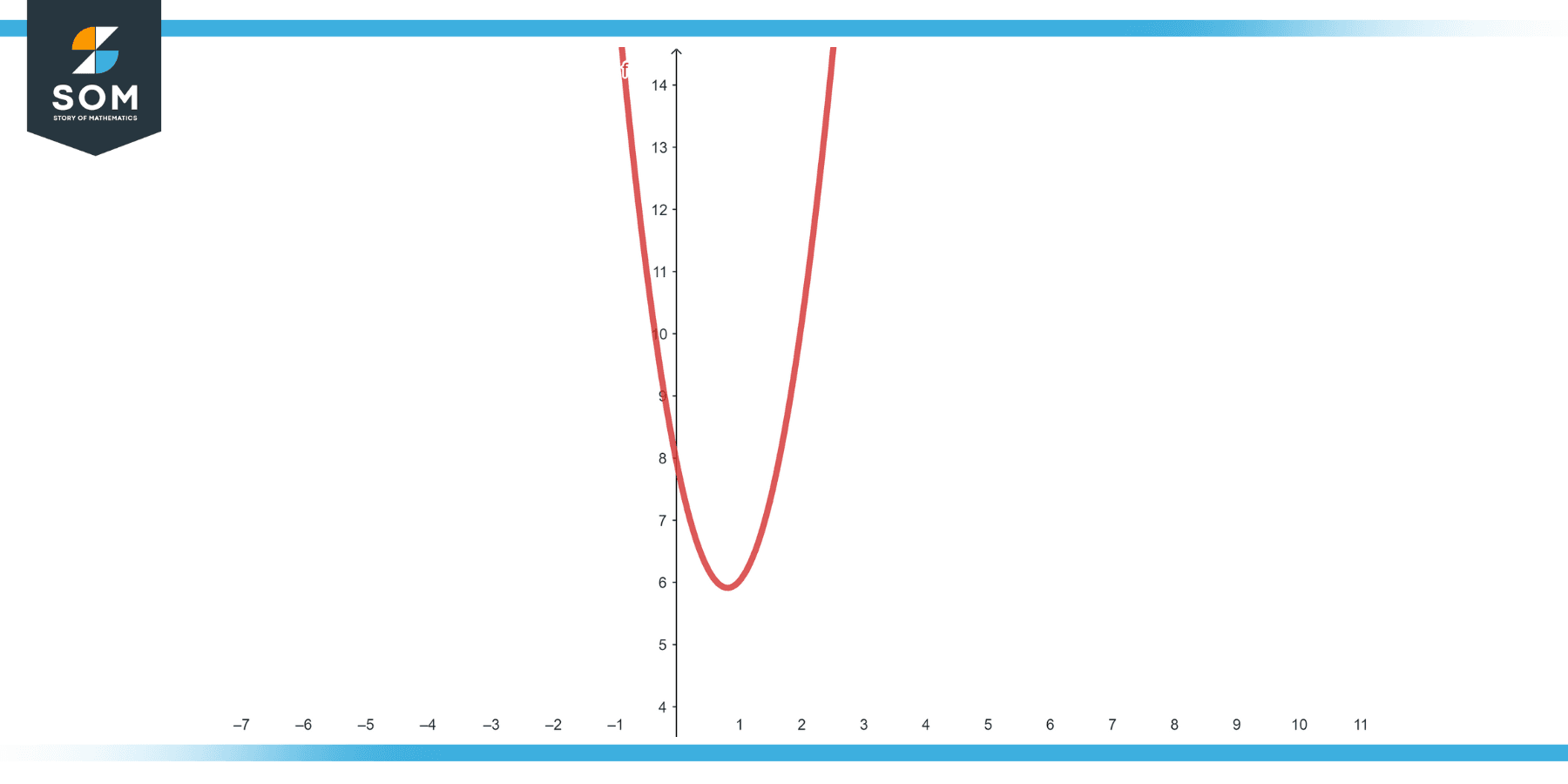
Figure-3.

Solution

This is a quadratic expression in terms of $y$. Its value depends on the value assigned to $y$. For example, if $y=2$, the value is:

3$(2^2)$$=10$.

Example 3

Equation: $2x+5=11$

Solution

To solve for $x$:

2x = 11−5

$2x=$6

$x=3$

Example 4

Equation $(y^2)$ $-4y+4=0$

Solution

This is a quadratic equation. Factorizing, $(y-2)(y-2)=0$ So, $y=2$ is the solution.

Applications 

Equations and expressions are foundational concepts in mathematics and thus find applications across numerous fields. Here’s how they’re used in various domains:

• Pure Mathematics

  • Expression: Mathematicians use expressions to define functions, such as $f(x)=\; \$(x^2)\$$ $+3x-7$. These functions can then be studied for their properties, like continuity or differentiability.
  • Equation: Equations like $(x^2)$ − 5x + 6 = 0 (quadratic equations) are solved to find values of $x$. In algebra, equations are used to prove theorems and solve for unknowns.

• Physics

  • Expression: Physical quantities, like kinetic energy (1/2 ​m$(v^2)$) or gravitational potential energy ($mgh$), are represented as expressions.
  • Equation: Equations describe laws of physics, such as Newton’s second law ($F=m\; *\; a$) or Einstein’s mass-energy equivalence (E=m$c^2$).

• Engineering

  • Expression: Engineers use expressions to represent quantities like stress, strain, and electrical resistance in a system.
  • Equation: Equations are essential in design calculations. For example, in electrical engineering, Ohm’s law ($V=IR$) is an equation used to relate voltage, current, and resistance.

• Economics

  • Expression: Expressions might represent economic variables like the utility function or production function.
  • Equation: Equations, like the equilibrium condition where supply equals demand, are pivotal in analyzing economic models and systems.

• Computer Science

  • Expression: In programming, expressions evaluate a value, such as arithmetic computations or string manipulations.
  • Equation: In some functional programming languages, equations define relationships between variables or functions. In algorithms, equations might describe relationships between variables or components.

• Biology and Medicine

  • Expression: Expressions might represent the rate of enzyme activity or the concentration of a solute in a solution.
  • Equation: Equations can model biological systems, like the Michaelis-Menten equation in enzyme kinetics or the exponential growth of bacterial populations.

• Finance

  • Expression: Financial metrics, like earnings before interest and taxes (EBIT) or net present value (NPV), can be represented as expressions.
  • Equation: In finance, equations are used to establish relationships, such as the one between different financial ratios or between present value and future value.

In all these fields and many more, expressions and equations allow professionals to represent, analyze, and predict various phenomena. The precise nature of their use depends on the specific requirements of each domain.

All images were created with GeoGebra.