JUMP TO TOPIC

The pentagonal prism is a captivating and versatile geometric shape that sparks interest in both the realms of mathematical theory and real-world application. As a three-dimensional figure, the pentagonal prism belongs to the family of prisms, characterized by two congruent bases and rectangular sides connecting the corresponding vertices. In the case of a pentagonal prism, its bases are pentagons, a five-sided polygon brimming with fascinating properties and symmetry. This unique shape plays a significant role in various fields, such as architecture, design, and science.
In this article, we explore the world of pentagonal prisms in great detail, looking at its distinctive features, mathematical properties, and wide-ranging applications. Get ready for an intriguing voyage into the universe of this five-sided prism as you learn about the beauty and complexity hidden within its deceptively straightforward shape.
Definition
A pentagonal prism is a three-dimensional geometric shape belonging to the broader class of prismatic solids, more specifically, to the family of prisms. As suggested by its name, this shape features pentagons as its bases. A pentagonal prism is defined by two congruent pentagonal bases that lie in parallel planes. Connecting these bases are five rectangular faces or lateral faces.
The term ‘prism’ in its name signifies that this geometric figure has identical cross-sections along its length if it is cut parallel to the bases. In simpler terms, if you slice a pentagonal prism parallel to its bases, each slice will be a pentagon identical to the base. This property is a defining feature of prisms. Below we present the generic diagram for the pentagonal prism.
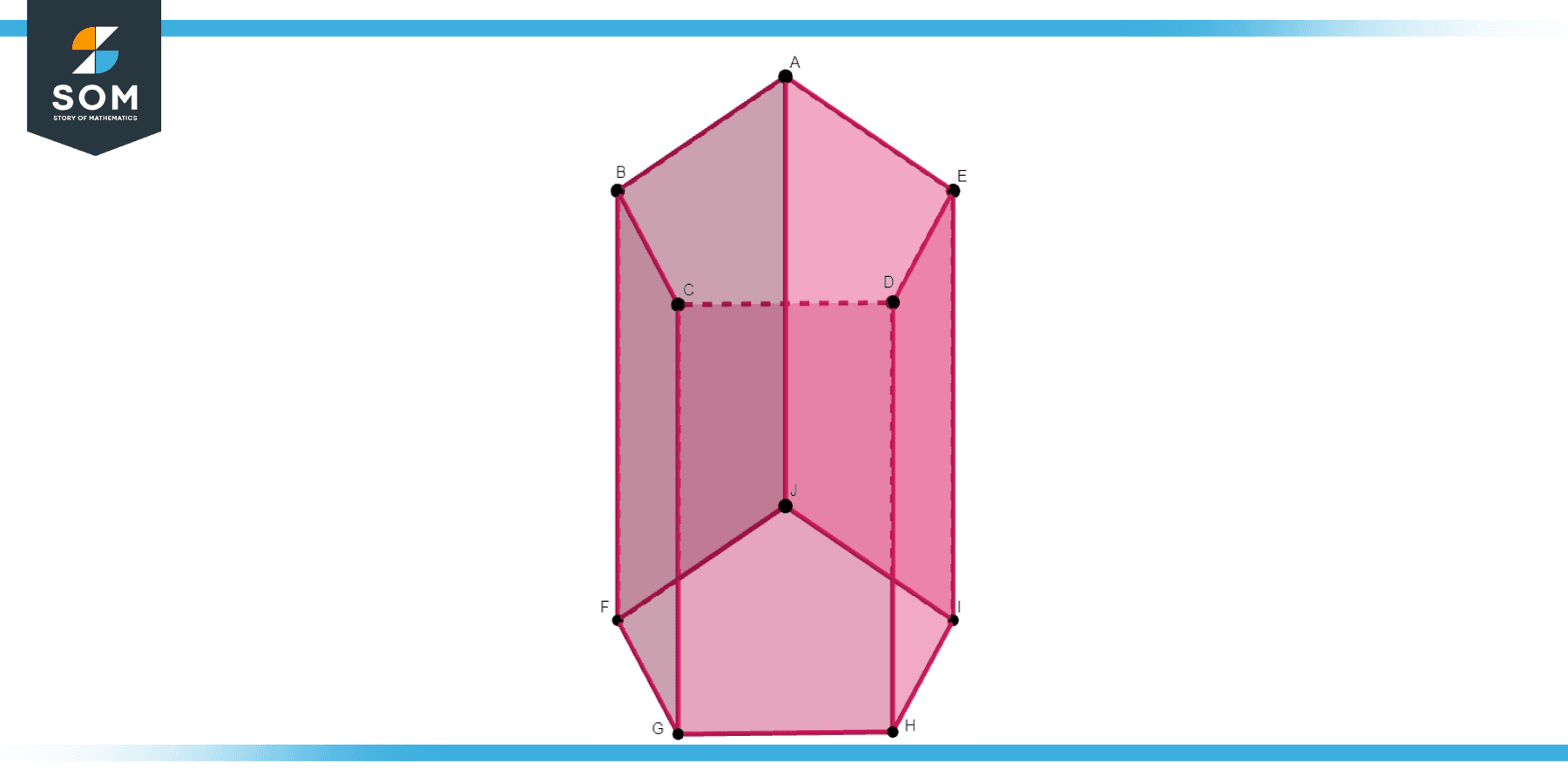
Figure-1: Generic pentagonal prism.
The beauty of a pentagonal prism is found not only in its unique shape but also in the interesting mathematical properties and real-world applications that it presents. From architecture to product design, pentagonal prisms form an integral part of our everyday world.
Historical Significance
The pentagonal prism is a fascinating geometric design with a long history that may be traced to early civilizations. Investigating its history reveals fascinating details about the development of geometry and its practical uses.
Greeks made substantial contributions to the subject of geometry and are credited with its origins. Euclid, a renowned Greek mathematician, documented the principles of geometry in his influential work, “Elements,” around 300 BCE. While Euclid did not specifically mention the pentagonal prism, his foundational work laid the groundwork for its understanding.
The concept of a prism, a polyhedron with two parallel and congruent polygonal bases connected by rectangular or parallelogram faces, existed in ancient Egypt. However, it was the Greeks who delved deeper into the properties of various prism shapes, including the pentagonal prism.
During the Hellenistic period, the study of solid geometry progressed further under mathematicians such as Archimedes and Apollonius of Perga. These scholars explored the properties of different prisms, including the pentagonal prism, and made significant contributions to their understanding.
The practical applications of prisms, including the pentagonal prism, gained prominence during the Renaissance era. Architects and builders, inspired by the mathematical principles of the ancient Greeks, incorporated geometric shapes into their designs. The pentagonal prism, with its unique properties, found its way into architectural structures, sculptures, and decorative art forms.
In modern times, the study and utilization of the pentagonal prism have expanded across various fields. Mathematicians, engineers, architects, and designers continue to explore its properties, such as volume, surface area, and symmetry. The advent of computer-aided design (CAD) and computational geometry has further facilitated the exploration and application of the pentagonal prism in diverse industries.
Today, the pentagonal prism remains a subject of fascination for mathematicians and serves as a geometric foundation for architectural and structural design. Its distinct shape and symmetrical properties make it an intriguing element in various creative endeavors, ranging from art and sculpture to product design and engineering.
The historical background of the pentagonal prism is rooted in the ancient world, with its understanding and application evolving over centuries. From the foundational work of Euclid to the contributions of Renaissance architects and contemporary mathematicians, the pentagonal prism continues to captivate minds and find its place in the realms of mathematics, art, and practical design.
Types
A pentagonal prism is a specific type of prism that has pentagonal bases; hence there aren’t specific “types” of pentagonal prisms as such. However, variations of the pentagonal prism can be distinguished based on the characteristics of its pentagonal bases and how it’s oriented. Here are some examples:
Regular Pentagonal Prism
This type of pentagonal prism has regular pentagons as its bases. A regular pentagon has all sides of equal length and all interior angles equal to 108 degrees. Therefore, in a regular pentagonal prism, all the edges are of equal length, and the rectangular faces are actually squares. Below we present the generic diagram for the regular pentagonal prism.
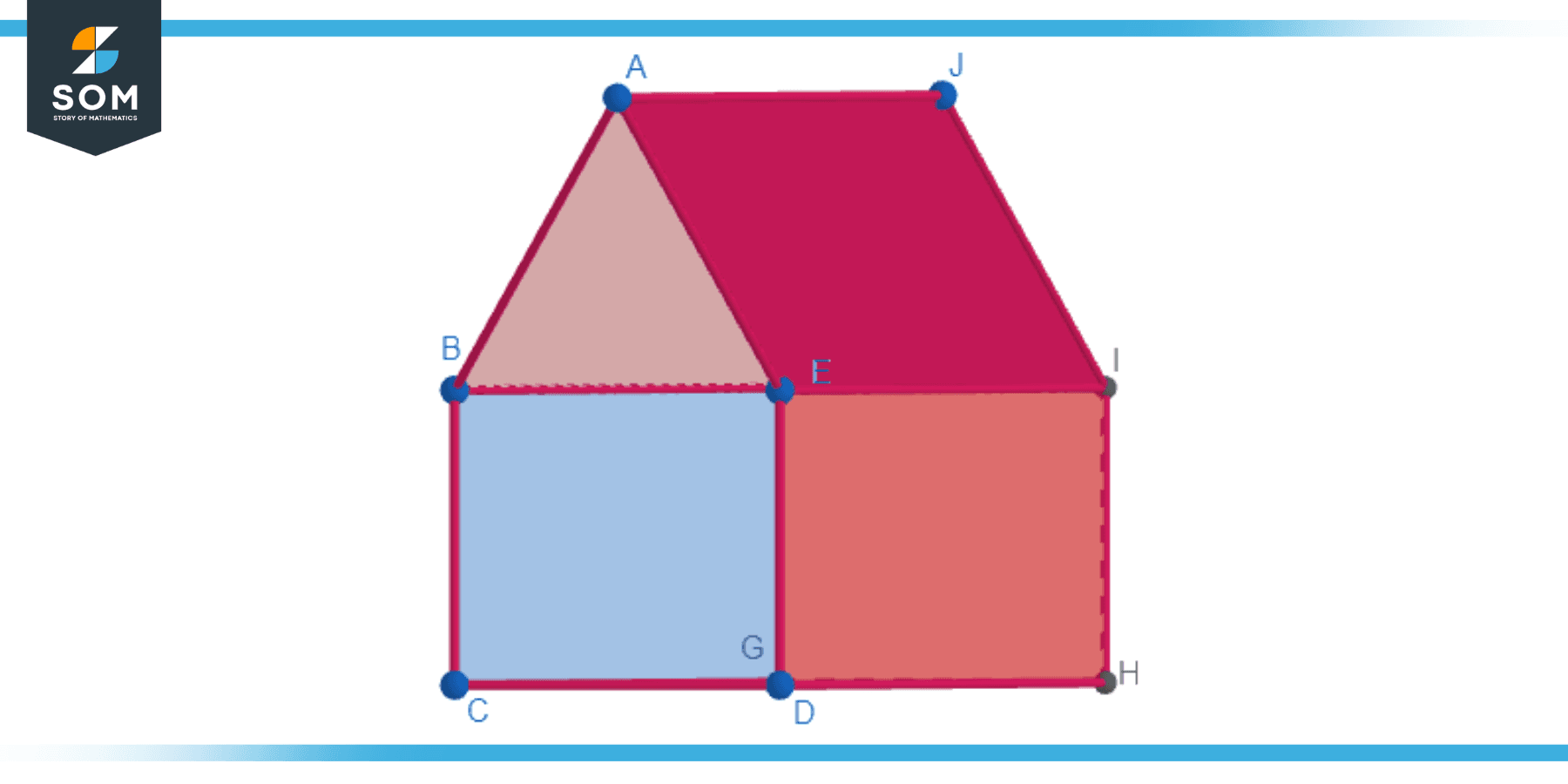
Figure-2: Regular pentagonal prism.
Irregular Pentagonal Prism
An irregular pentagonal prism has irregular pentagons as its bases. In an irregular pentagon, the sides and angles are not necessarily equal. Therefore, in an irregular pentagonal prism, the rectangular faces can be rectangles of different dimensions. Below we present the generic diagram for the irregular pentagonal prism.
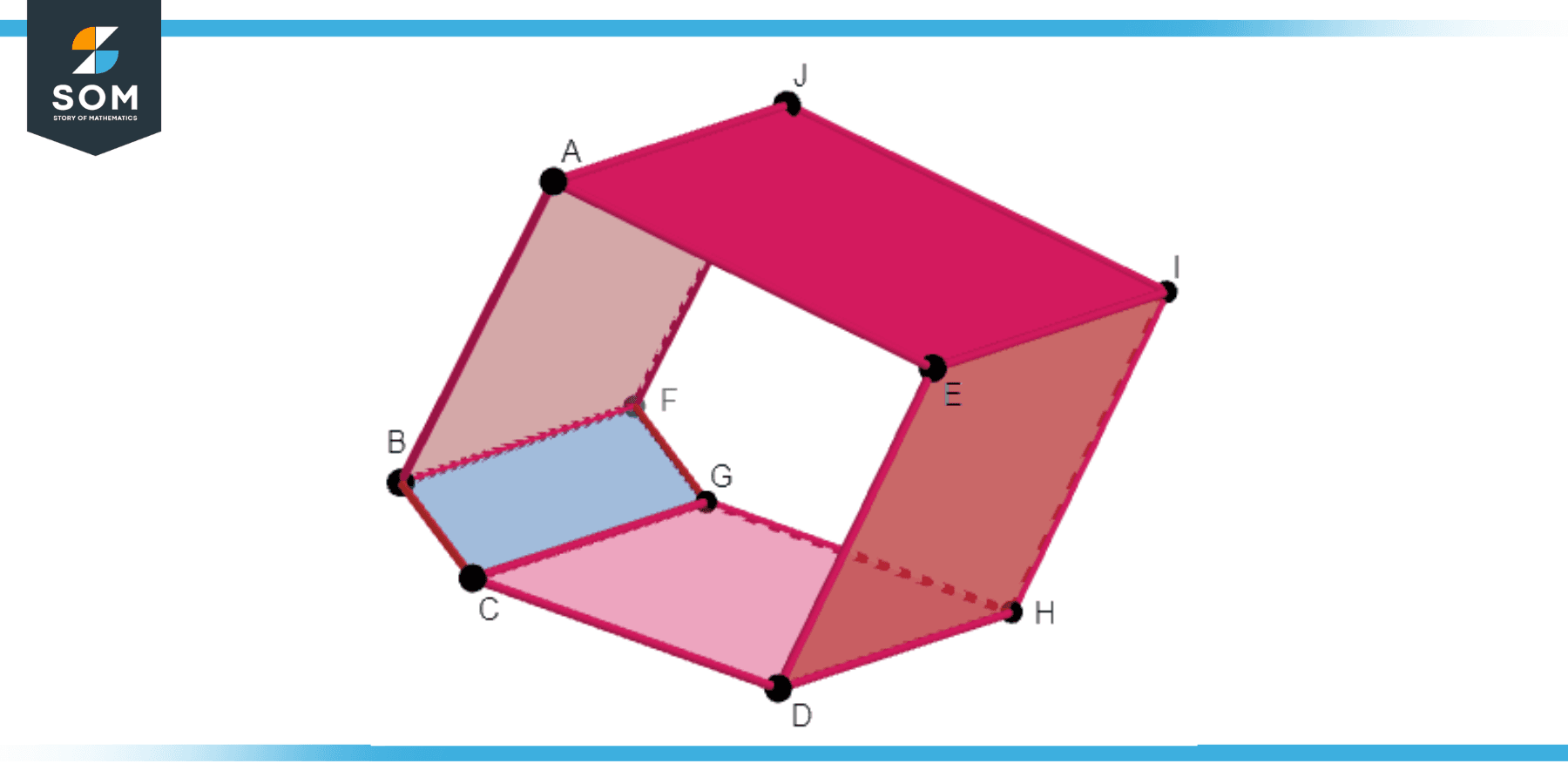
Figure-3: Irregular pentagonal prism.
Oblique Pentagonal Prism
An oblique pentagonal prism is a pentagonal prism where the line joining the centers of the bases (the axis) is not perpendicular to the bases. This means the bases are not directly above each other, giving the prism a slanted appearance. Below we present the generic diagram for the oblique pentagonal prism.
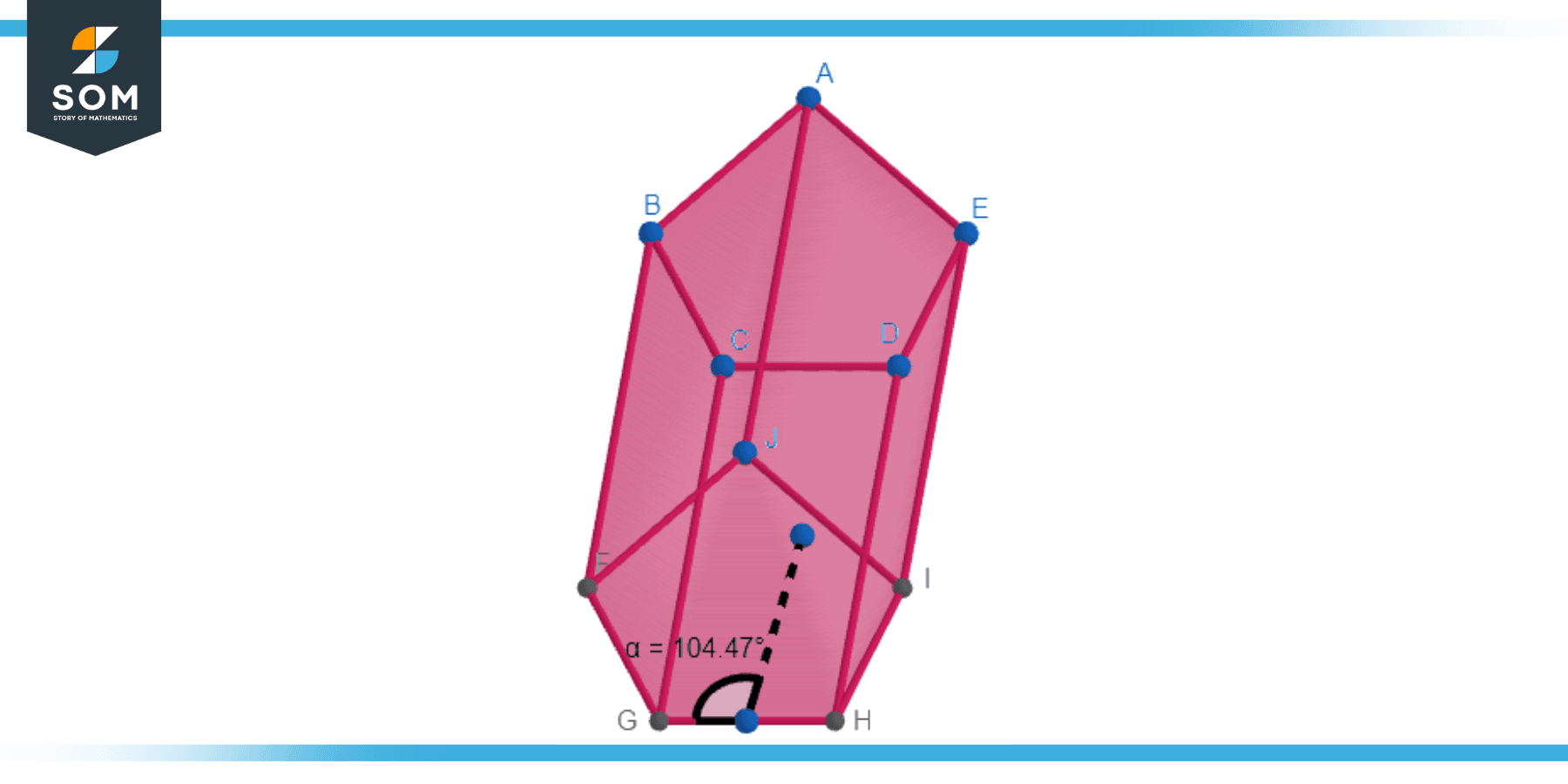
Figure-4: Oblique pentagonal prism.
Right Pentagonal Prism
A right pentagonal prism is a pentagonal prism where the line joining the centers of the bases (the axis) is perpendicular to the bases. This means the bases are directly aligned above each other, giving the prism a straight, upright appearance. Below we present the generic diagram for the right pentagonal prism.
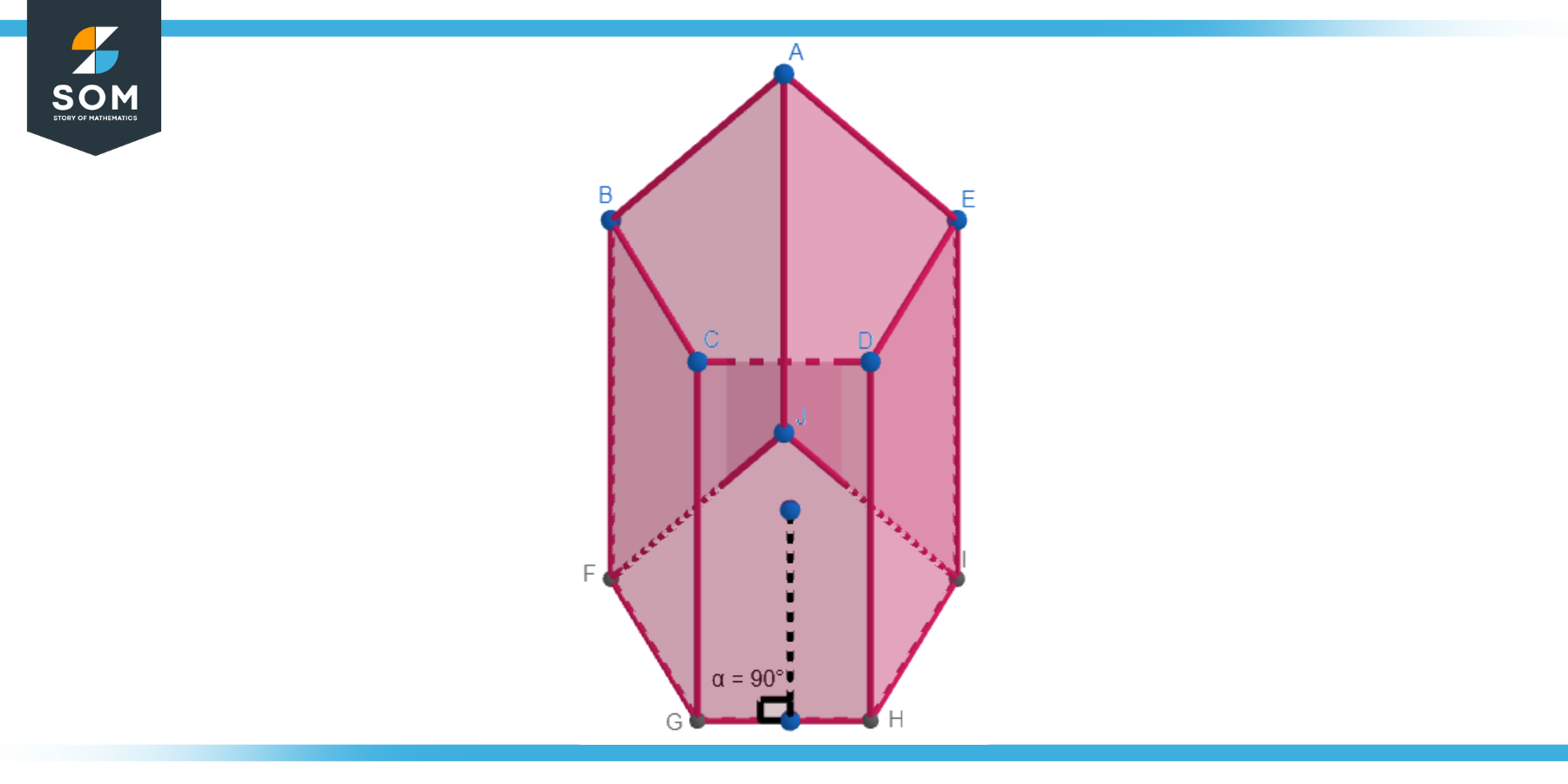
Figure-5: Right pentagonal prism.
Please note the characteristics of a pentagonal prism, such as its volume and surface area, can be calculated based on the lengths of its sides, the height of the prism, and the nature of its bases (whether they’re regular or irregular).
Properties
A pentagonal prism, like any other prism, has a variety of geometric properties that define its shape and structure. Here are some key properties:
Bases
A pentagonal prism has two bases that are pentagonal in shape. The bases are congruent, meaning they are identical in size and shape.
Faces
A pentagonal prism has seven faces – two pentagonal faces (the bases) and five rectangular faces.
Edges
A pentagonal prism has 15 edges. Each edge is where two faces meet. The edges are formed by five rectangles and two pentagons.
Vertices
A pentagonal prism has 10 vertices. A vertex is a point where three or more edges meet.
Cross-Section
The cross-section of a pentagonal prism is a pentagon. This means if you were to slice the prism parallel to the bases, the resulting shape would be a pentagon.
Regular vs. Irregular
If the pentagonal bases are regular pentagons (all sides and angles are equal), then it’s called a regular pentagonal prism. If the bases are not regular, it’s called an irregular pentagonal prism.
Right vs. Oblique
If the line joining the centers of the bases (the axis) is perpendicular to the bases, then it’s a right pentagonal prism. If the axis is not perpendicular to the bases, it’s an oblique pentagonal prism.
Volume
The volume of a pentagonal prism can be calculated using the formula: V = B × h, where B is the area of the base (the pentagon) and h is the height of the prism.
Surface Area
The surface area of a pentagonal prism can be calculated using the formula: A = 2 × B + P × h, where B is the area of the base, P is the base’s perimeter, and h is the height of the prism. The term 2B gives the combined area of the bases, and Ph gives the total area of the rectangular faces.
The above properties help us understand the characteristics of a pentagonal prism and aid in solving geometric problems involving this shape.
Ralevent Formulas
A pentagonal prism has several associated formulas that are used to calculate its various geometric properties. Here are the key ones:
Volume
The volume of a pentagonal prism (or any prism) is given by the formula:
V = B × h
where, V is the volume, B is the area of the base (in this case, a pentagon), and h is the height of the prism (the distance between the two bases).
Area
If the base is a regular pentagon with side length a, then the area of the base B can be calculated by:
B = 5/4 × a² × cot(π/5)
Surface Area
The surface area of a pentagonal prism is the sum of the areas of all its faces. The formula is:
A = 2B + P × h
where, A is the surface area, B is the area of the base (calculated as above), P is the perimeter of the base (for a regular pentagon, P = 5a where a is the length of a side), and h is the height of the prism. The term 2B gives the combined area of the bases, and P × h gives the total area of the rectangular faces.
Diagonal Length
If you need to find the length of the space diagonal (the longest diagonal of the prism, stretching from one corner to the opposite corner through the interior), the formula for a right pentagonal prism is:
d = √(a² + 2h²)
where, d is the length of the space diagonal, a is the side length of the pentagonal base, and h is the height of the prism.
Applications
The pentagonal prism, with its unique geometric properties, finds applications in various fields, ranging from mathematics and architecture to engineering and design. Let’s explore some key applications.
Mathematics and Geometry Education
The pentagonal prism serves as an excellent educational tool to teach and understand geometric concepts. It helps students grasp the principles of polyhedra, surface area, volume, symmetry, and spatial visualization.
Architecture and Structural Design
The pentagonal prism’s distinctive shape and symmetrical properties make it an intriguing element in architectural design. It can be incorporated into building facades, interior spaces, and decorative elements to create visually appealing structures.
Optics and Physics
In optics, the pentagonal prism can be used as a component in light dispersion and beam manipulation. It can separate white light into its constituent colors, demonstrating the dispersion of light and the creation of spectral patterns.
Product Design and Packaging
The pentagonal prism‘s aesthetic appeal and structural stability make it an ideal choice in product design. It can be utilized in the creation of unique packaging solutions, decorative objects, and display cases.
3D Modeling and Computer Graphics
The pentagonal prism is commonly employed in computer graphics and 3D modeling applications. Its geometry serves as a building block for creating complex 3D shapes and structures.
Robotics and Engineering
In robotics, the pentagonal prism can be used as a foundational component in the construction of robotic arms, grippers, and other mechanical systems. Its symmetrical design allows for efficient movement and structural stability.
Mathematics and Mathematical Research
The pentagonal prism holds significance in mathematical research and exploration. It serves as a subject of study for mathematicians investigating topics such as symmetry groups, polyhedral combinatorics, and geometric transformations.
Art and Sculpture
Artists and sculptors incorporate the pentagonal prism’s distinct shape into their creations. It adds complexity, visual interest, and a sense of geometric harmony to sculptures, installations, and artistic compositions.
Packaging
The pentagonal prism is also commonly used in packaging design. For instance, some types of boxes or containers, especially for high-end products, use this shape to create a unique and appealing look.
Furniture Design
In furniture design, the pentagonal prism is sometimes used for creating distinctive items like stools, tables, or bookshelves.
Jewelry Design
Gemstones are often cut in the shape of a pentagonal prism. This shape allows for an attractive play of light and creates a striking visual appeal.
These are just a few examples of the diverse applications of the pentagonal prism across various fields. Its unique geometry, symmetries, and structural properties make it a versatile and captivating shape that continues to inspire innovation and creativity in different disciplines.
Exercise
Example 1
Volume Calculation
Calculate the volume of a right regular pentagonal prism with a side length of 5 cm and height 10 cm.
Solution
First, calculate the area of the base. For a regular pentagon with side length a, the area is given by:
B = 5/4 × a² × cot(π/5)
Here, a = 5 cm, so B = 5/4 × 5² × cot(π/5) = 30.9 cm².
Volume V is given by:
V = B × h
Here, h = 10 cm, so V = 30.9 × 10 = 309 cm³.
Example 2
Surface Area Calculation
Calculate the surface area of a right regular pentagonal prism with a side length of 4 cm and height 12 cm.
Solution
First, calculate the area of the base, B, and the perimeter of the base:
B = 5/4 × 4² × cot(π/5)
B = 19.7 cm²
P = 5 × 4 = 20 cm
The surface area A is given by:
A = 2 × B + P × h
Here, h = 12 cm, so A = 2 × 19.7 + 20 × 12 = 304.4 cm².
Example 3
Space Diagonal Calculation
Calculate the length of the space diagonal of a right regular pentagonal prism with a side length of 6 cm and height of 8 cm.
Solution
The length of the space diagonal d is given by:
d = √(a² + 2h²)
Here, a = 6 cm and h = 8 cm, so d = √(6² + 2 × 8²) = 14 cm.
Example 4
Irregular Pentagonal Prism Volume
Calculate the volume of a right pentagonal prism with a base area of 7 cm² and height of 10 cm.
Solution
The volume V of a prism is given by :
V = B × h
Here, B = 7 cm² and h = 10 cm, so we get:
V = 7 × 10
V = 70 cm³
Example 5
Irregular Pentagonal Prism Surface Area
Calculate the surface area of a right pentagonal prism with a base perimeter of 18 cm, base area of 12 cm², and height of 15 cm.
Solution
The surface area A of a prism is given by:
A = 2 × B + P × h
Here, B = 12 cm², P = 18 cm, and h = 15 cm, so we get:
A = 2 × 12 + 18 × 15
A = 312 cm²
Example 6
Height Calculation
Find the height of a right regular pentagonal prism with a side length of 3 cm and volume of 135 cm³.
Solution
The volume V of a prism is given by V = B × h, so h = V / B. First, calculate the area of the base:
B = 5/4 × 3² × cot(π/5)
B = 11 cm²
Here, V = 135 cm³, so h = 135 / 11 = 12.3 cm.
Example 7
Base Side Length Calculation
Find the side length of a right regular pentagonal prism with a height of 10 cm and a surface area of 150 cm².
Solution
The surface area A of a prism is given by A = 2 × B + P × h, and the base perimeter:
P = 5 × a
so
5 × a = (A – 2 × B) / h
Here, h = 10 cm and A = 150 cm², but we don’t know B because we don’t know a. However, B and P are both proportional to a², so (A – 2B) / h is also proportional to a, meaning we can write it as ka for some constant k. This gives us:
5 × a = k × a
so
k = 5
and
a = √((A / (2k)) / cot(π/5))
Substituting A = 150 cm² and k = 5, we find a = 3.5 cm.
Example 8
Oblique Prism Height
An oblique pentagonal prism has a base side length of 5 cm, a height along the edge of 12 cm, and a space diagonal of 15 cm. Find the true height (the perpendicular distance between the bases).
Solution
The space diagonal d of a prism is given by d = √(a² + 2h²). Here, d = 15 cm, and a = 5 cm, so we can solve for h:
2 × h² = d² – a²
2 × h² = 15² – 5²
2 × h² = 200
so h = √(200 / 2) = 10 cm. The true height of the prism is 10 cm.
All images were created with GeoGebra.
